
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{9}{6}=\frac{3\times 3}{3\times 2}=\frac{3}{2}$
$\frac{4}{6}=\frac{2\times 2}{3\times 2}=\frac{2}{3}$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

Lời giải:
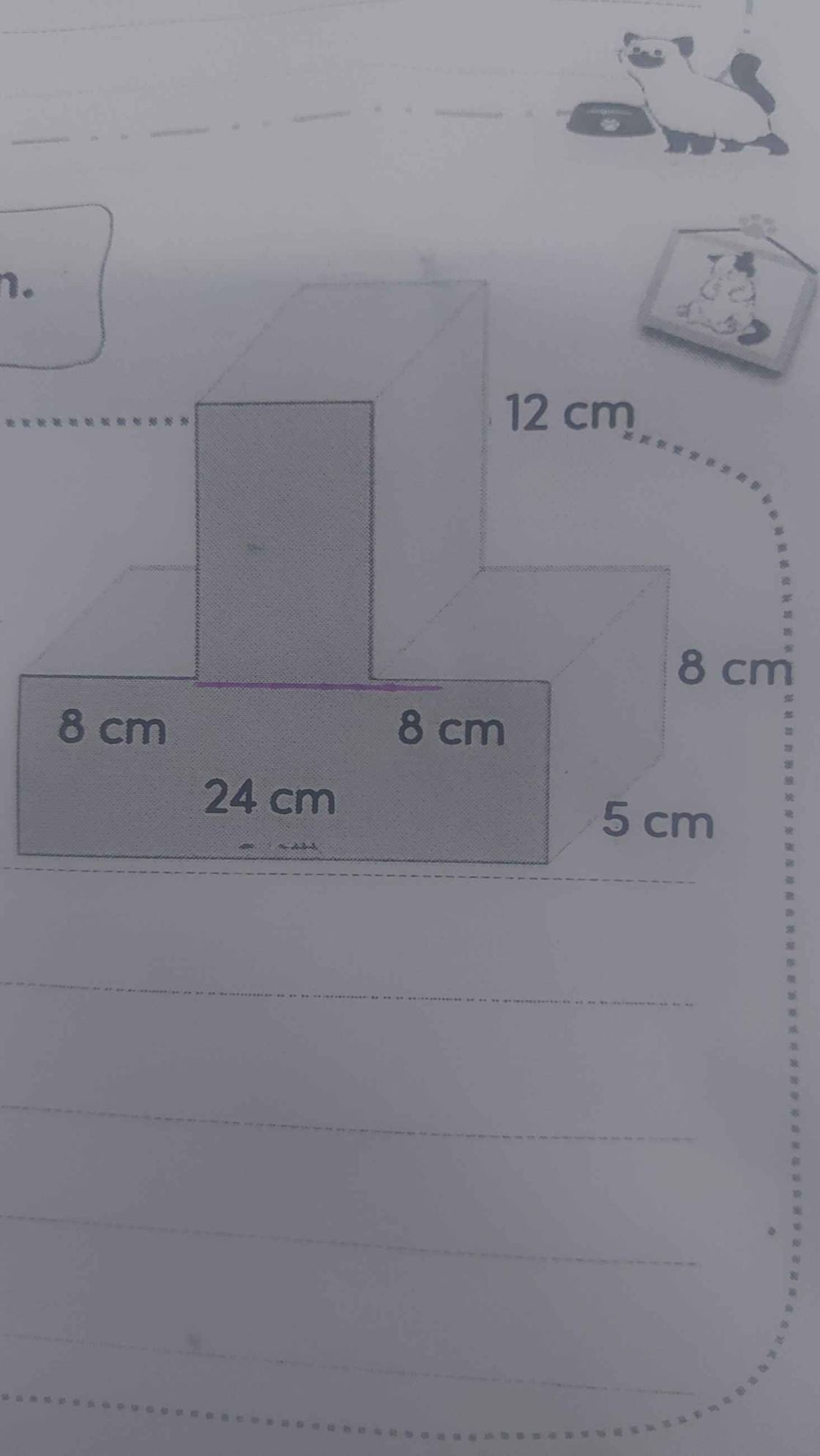
Gọi khối hcn ở trên là $A$ và khối hcn bên dưới là $B$.
Chiều rộng khối A: $5$ (cm)
Chiều cao khối A: $12$ (cm)
Chiều dài khối A: $24-8-8=8$ (cm)
Thể tích khối A: $5\times 12\times 8=480$ (cm3)
Thể tích khối B: $24\times 5\times 8=960$ (cm3)
Thể tích hình vẽ: $480+960=1440$ (cm3)

Ta có:
\(\dfrac{3}{6}=\dfrac{3\cdot3}{6\cdot3}=\dfrac{9}{18}\)
\(\dfrac{3}{18}=\dfrac{3}{18}\)
Vậy quy đồng mẫu số 2 phân số \(\dfrac{2}{6}\) và \(\dfrac{3}{18}\) ta được \(\dfrac{9}{18}\) và \(\dfrac{3}{18}\)

Từ đường tròn lượng giác ta thấy trên khoảng \(\left(-\dfrac{3\pi}{2};3\pi\right)\) phương trình \(sinx=k\)
- Có 5 nghiệm khi \(0< k< 1\)
- Có 4 nghiệm khi \(-1< k\le0\)
- Có 2 nghiệm khi \(k=1\)
- Có 2 nghiệm khi \(k=-1\)
Vậy pt đã cho có 9 nghiệm khi
TH1: \(\left\{{}\begin{matrix}0< -3m< 1\\-1< m-2\le0\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}0< m-2< 1\\-1< -3m\le0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2< m< 3\\0\le m< \dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow m\in\varnothing\)
A đúng
Từ đường tròn lượng giác ta thấy trên khoảng phương trình
- Có 5 nghiệm khi
- Có 4 nghiệm khi
- Có 2 nghiệm khi
- Có 2 nghiệm khi
Vậy pt đã cho có 9 nghiệm khi
TH1:
TH2:
A đúng

\(\prod\limits^{ }_{\cot\int\limits^{ }_{ }dx\lim\limits_{ }\sqrt[]{}^{ }\sqrt[]{}\sqrt{ }\sqrt{ }\sqrt[]{}}\)

Số điểm còn lại là 300-30=270(điểm)
TH1: Lấy 1 điểm trong 30 điểm thẳng hàng, 1 điểm trong 270 điểm còn lại
=>Có \(30\cdot270=8100\left(đường\right)\)
TH2: Vẽ đường thẳng đi qua 30 điểm thẳng hàng
=>Có 1 đường
TH3: Lấy 2 điểm bất kì trong 270 điểm còn lại
=>Có \(C^2_{270}=36315\left(đường\right)\)
Tổng số đường thẳng vẽ được là:
36315+1+8100=44416(đường)

Bài 2:
Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
Bài 3:
a: Xét tứ giác MKHN có \(\widehat{MKN}=\widehat{MHN}=90^0\)
nên MKHN là tứ giác nội tiếp
b: Xét tứ giác PHIK có \(\widehat{PHI}+\widehat{PKI}=90^0+90^0=180^0\)
nên PHIK là tứ giác nội tiếp

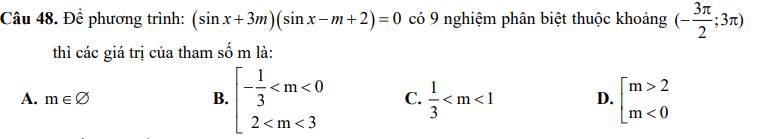


a: Xét ΔABD vuông tại A và ΔAHD vuông tại H có
AD chung
\(\widehat{BAD}=\widehat{HAD}\)
Do đó: ΔABD=ΔAHD
b: Ta có: ΔABD=ΔAHD
=>AB=AH và DB=DH
Ta có: AB=AH
=>A nằm trên đường trung trực của BH(1)
Ta có: DB=DH
=>D nằm trên đường trung trực của BH(2)
Từ (1),(2) suy ra AD là đường trung trực của BH
c: Xét ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
\(\widehat{BDI}=\widehat{HDC}\)(hai góc đối đỉnh)
Do đó: ΔDBI=ΔDHC
=>DI=DC
=>ΔDIC cân tại D
d: Ta có: ΔDBI=ΔDHC
=>BI=HC
Xét ΔAIC có \(\dfrac{AB}{BI}=\dfrac{AH}{HC}\)
nên BH//CI
e: Ta có: AB+BI=AI
AH+HC=AC
mà AB=AH và BI=HC
nên AI=AC
=>A nằm trên đường trung trực của CI(3)
Ta có: DI=DC
=>D nằm trên đường trung trực của CI(4)
Từ (3) và (4) suy ra AD là đường trung trực của CI
=>AD\(\perp\)CI