
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian ô tô thứ nhất đi từ A đến B là \(\dfrac{x}{30}\left(giờ\right)\)
Thời gian ô tô thứ hai đi từ A đến B là \(\dfrac{x}{60}\left(giờ\right)\)
Ô tô thứ hai đến B trước ô tô thứ nhất 3 giờ nên ta có:
\(\dfrac{x}{30}-\dfrac{x}{60}=3\)
=>\(\dfrac{x}{60}=3\)
=>x=180(nhận)
Thời gian ô tô thứ nhất đi là 180/60=3(giờ)
Thời gian ô tô thứ hai đi là 180/30=6(giờ)

Bài 2:\(A\left(x\right)=2x^2-3x+1\)
\(A\left(-2\right)=2\cdot\left(-2\right)^2-3\cdot\left(-2\right)+1=8+6+1=15\)
Bài 3:
a: A(x)+B(x)
\(=2x^2-4x+1+x^2+2x-2\)
\(=3x^2-2x-1\)
b: A(x)-B(x)
\(=2x^2-4x+1-x^2-2x+2\)
\(=x^2-6x+3\)
Bài 5:
a:, Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>BA=BH và EA=EH
Ta có:BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: EA=EH
=>E nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra BE là đường trung trực của AH
c: Ta có: EH=EA
mà EA<EK(ΔEAK vuông tại A)
nên EH<EK

A(\(x\)) = 2\(x^2\) - 3\(x\) + 1
A(-2) = 2.(-2)2 - 3.(-2) + 1
A(-2) = 2.4 + 6 + 1
A(-2) = 8 + 6 + 1
A(-2) = 15

Đặt P(x)=0
=>\(8x^2+4x+7=0\)
\(\text{Δ}=4^2-4\cdot8\cdot7=-208< 0\)
=>P(x) không có nghiệm

a: Số chai nước hoa quả trong 20 thùng là:
20x(chai)
b: Chu vi là \(2\left(a+2\right)=2a+4\left(cm\right)\)

a: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=30^0\)
Xét ΔADB có \(\widehat{ADB}+\widehat{BAD}+\widehat{ABD}=180^0\)
=>\(\widehat{ADB}+30^0+80^0=180^0\)
=>\(\widehat{ADB}=70^0\)
b: Xét ΔABD có \(\widehat{BAD}< \widehat{ADB}< \widehat{ABD}\)
mà BD,AB,AD lần lượt là các cạnh đối diện của các góc BAD,ADB,ABD
nên BD<AB<AD
c: Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ACB}+60^0+80^0=180^0\)
=>\(\widehat{ACB}=40^0\)
ta có: \(\widehat{ADB}+\widehat{ADC}=180^0\)
=>\(\widehat{ADC}+70^0=180^0\)
=>\(\widehat{ADC}=110^0\)
Xét ΔADC có \(\widehat{DAC}< \widehat{DCA}< \widehat{ADC}\)
mà DC,DA,AC lần lượt là cạnh đối diện của các góc DAC,DCA,ADC
nên DC<DA<AC

a: \(5x\left(12x+7\right)-3x\left(20x-5\right)=-100\)
=>\(60x^2+35x-60x^2+15x=-100\)
=>50x=-100
=>x=-2
b: \(\left(2x-1\right)\left(3x+1\right)+\left(3x+4\right)\left(3-2x\right)=5\)
=>\(6x^2+2x-3x-1+9x-6x^2+12-8x=5\)
=>11=5(loại)
c: \(6x^2-\left(2x-5\right)\left(3x-2\right)=7\)
=>\(6x^2-\left(6x^2-4x-15x+10\right)=7\)
=>19x-10=7
=>19x=17
=>\(x=\dfrac{17}{19}\)
d: \(\left(x-3x^2\right)\left(x+6\right)+x\left(3x^2+17x\right)=24\)
=>\(x^2+6x-3x^3-18x^2+3x^3+17x^2=24\)
=>6x=24
=>x=4
e: \(\left(x-1\right)\left(x^2+x+1\right)+9=0\)
=>\(x^3-1+9=0\)
=>\(x^3+8=0\)
=>\(x^3=-8\)
=>x=-2
f: \(\left(12x-5\right)\left(4x-1\right)-\left(3x-7\right)\left(16x+1\right)=81\)
=>\(48x^2-12x-20x+5-\left(48x^2+3x-112x-7\right)=81\)
=>-32x+5+109x+7=81
=>77x=81-12=69
=>\(x=\dfrac{69}{77}\)



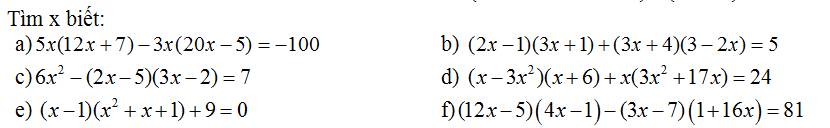


a: Xét ΔAIB và ΔAIC có
AB=AC
BI=CI
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔABI=ΔACI
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
Xét ΔDBC có
DI là đường cao
DI là đường trung tuyến
Do đó: ΔDBC cân tại D
=>DB=DC
c: Ta có: DB=DE
mà D nằm giữa B và E
nên D là trung điểm của BE
Xét ΔEBC có
EI,CD là các đường trung tuyến
EI cắt CD tại G
Do đó: G là trọng tâm của ΔEBC
=>EG=2GI