Vào tháng 1, giá niêm yết của một chiếc tivi tại một siêu thị A là 45000000 đồng. Đến tháng 2, siêu thị giảm giá 20% cho mỗi chiếc tivi. Sang tháng 3, siêu thị lại giảm giá thêm một lần nữa, lúc này giá của chiếc tivi chỉ còn 34200000 đồng. Hỏi tháng 3, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc tv so với tháng 2?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>AD=AE
=>ΔADE cân tại A
ΔADB=ΔAEC
=>DB=EC
b: Xét ΔADK vuông tại D và ΔAEK vuông tại E có
AK chung
AD=AE
Do đó: ΔADK=ΔAEK
=>\(\widehat{DAK}=\widehat{EAK}\)
=>AK là phân giác của góc DAE
c: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại K
Do đó: K là trực tâm của ΔABC
=>AK\(\perp\) BC

a: \(M\left(x\right)=3x^4-5x^2-2x^3-4x+6x^2+8x^3-2\)
\(=3x^4+\left(-2x^3+8x^3\right)+\left(6x^2-5x^2\right)-4x-2\)
\(=3x^4+6x^3+x^2-4x-2\)
\(N\left(x\right)=\sqrt{2}x^4+\dfrac{1}{2}x^2-3x^3-\sqrt{2}x^4+5x^3-\dfrac{3}{2}x^2-4x-3\)
\(=\left(\sqrt{2}x^4-\sqrt{2}x^4\right)+\left(-3x^3+5x^3\right)+\left(\dfrac{1}{2}x^2-\dfrac{3}{2}x^2\right)-4x-3\)
\(=2x^3-x^2-4x-3\)
b: G(x)=M(x)+N(x)
\(=3x^4+6x^3+x^2-4x-2+2x^4-x^2-4x-3\)
\(=5x^4+6x^3-8x-5\)
c: H(x)=M(x)-N(x)
\(=3x^4+6x^3+x^2-4x-2-2x^4+x^2+4x+3\)
\(=x^4+6x^3+2x^2+1\)

\(-x^2\left(x^2-4x+3\right)+x\left(x^2+x-3\right)\)
\(=-x^4+4x^3-3x^2+x^3+x^2-3x\)
\(=-x^4+5x^3-2x^2-3x\)

A=(x-5)(x+7)-7x(x+3)
\(=x^2+7x-5x-35-7x^2-21x\)
\(=-6x^2-19x-35\)
(x - 5)(x + 7) - 7x(x + 3)
= x² + 7x - 5x - 35 - 7x² - 21x
= (x² - 7x²) + (7x - 5x - 21x) - 35
= -6x² - 19x - 35

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
=>AH là đường trung tuyến của ΔABC
b: Sửa đề: N là trung điểm của AC
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC
c: Xét ΔABC có
BN,AH là các đường trung tuyến
BN cắt AH tại K
Do đó: K là trọng tâm của ΔABC
Xét ΔABC có
K là trọng tâm
M là trung điểm của AB
Do đó: C,K,M thẳng hàng

\(P\left(x\right)=-2x^2+3x^4+x^3+x^2-\dfrac{1}{4}x\)
\(=3x^4+x^3+\left(-2x^2+x^2\right)-\dfrac{1}{4}x\)
\(=3x^4+x^3-x^2-\dfrac{1}{4}x\)
Khi x=-1 thì \(P\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3-\left(-1\right)^2-\dfrac{1}{4}\cdot\left(-1\right)\)
=3-1-1+1/4
=3+1/4
=3,25


a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
b: ta có: ΔNMI=ΔNKI
=>IM=IK
mà IK<IP(ΔIKP vuông tại K)
nên IM<IP
c: Xét ΔIMQ vuông tại M và ΔIKP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)(hai góc đối đỉnh)
Do đó: ΔIMQ=ΔIKP
=>IQ=IP
=>ΔIQP cân tại I
Xét ΔNQP có
QK,PM là các đường cao
QK cắt PM tại I
Do đó: I là trực tâm của ΔNQP
=>NI\(\perp\)PQ tại D
=>ND\(\perp\)PQ

a: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
mà AB,AC,BC lần lượt là cạnh đối diện của các góc ACB,ABC,BAC
nên AB<AC<BC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
c: ΔBAE=ΔBHE
=>BA=BH
Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
\(\widehat{HBK}\) chung
Do đó: ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
Xét ΔBKC cân tại B có \(\widehat{KBC}=60^0\)
nên ΔBKC đều

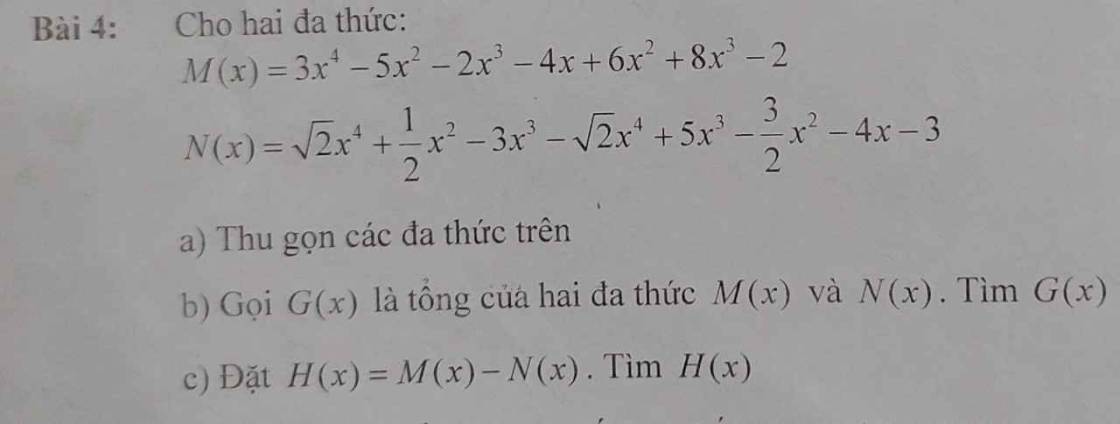

Giá tiền của 1 tivi trong tháng 2 là:
\(45000000\left(1-20\%\right)=36000000\left(đồng\right)\)
Số tiền giảm trong tháng 3 là:
36000000-34200000=1800000(đồng)
Phần trăm đã giảm so với tháng 2 là:
\(\dfrac{1800000}{36000000}=5\%\)