ai giúp mình với😥

B = \(\dfrac{1}{2^3}\) + \(\dfrac{2}{3^3}\) + \(\dfrac{3}{4^3}\)+...+ \(\dfrac{n-1}{n^3}\) (n > 2)

Vì n > 2 ⇒ B > 0 (1)

   \(\dfrac{1}{2^3}\) < \(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)

    \(\dfrac{2}{3^3}\) < \(\dfrac{3}{3^3}\) = \(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)

    \(\dfrac{3}{4^3}\)  <  \(\dfrac{4}{4^3}\) =  \(\dfrac{1}{4^2}\) < \(\dfrac{1}{3.4}\) = \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)

     ..................................................

    \(\dfrac{n-1}{n^3}\)<\(\dfrac{n^{ }}{n^3}\)  = \(\dfrac{1}{n^2}\) < \(\dfrac{1}{\left(n-1\right).n}\) = \(\dfrac{1}{n-1}\) - \(\dfrac{1}{n}\)

Cộng vế với vế ta có: 

 B <  1 - \(\dfrac{1}{n}\) < 1 (2)

Kết hợp (1) và(2) ta có: 0 < B < 1

Vậy B không phải là số tự nhiên (đpcm)

Ta có: \(A=\dfrac{x+1}{x-2}=\dfrac{x-2+3}{x-2}=\dfrac{x-2}{x-2}+\dfrac{3}{x-2}=1+\dfrac{3}{x-2}\)

Để A là số nguyên thì \(x-2\inƯ\left(3\right)=\left\{-1,-3,1,3\right\}\)

Ta có bảng giá trị:

Vậy ...

Ta có : \(A=\dfrac{x+1}{x-2}=\dfrac{x-2+3}{x-2}\)

\(\Rightarrow A=1+\dfrac{3}{x-2}\)

Vì x là số nguyên nên để A cũng là số nguyên thì : \(\dfrac{3}{x-2}\in Z\)

\(\Rightarrow3⋮\left(x-2\right)\)

\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)\)

Do đó ta có bảng :

Vậy..........

82x+1 – 8x = 3584 

=> 8x+1 = 3584 

8x+1 = 84 

x = 4-1 

x = 3 

Chúc bạn học tốt 

Có nhiều nguyên tố bao gồm:

Canxi (Ca): Canxi là một nguyên tố cần thiết cho sự phát triển và duy trì sức khỏe của xương. Nó giúp tạo ra và bảo vệ cấu trúc xương, đồng thời tham gia vào quá trình tạo mới và phân giải xương. Việc cung cấp đủ canxi cho cơ thể từ thức ăn và bổ sung canxi phù hợp có thể đảm bảo sự phát triển tối đa chiều cao.

Iốt (I): Iốt là một thành phần chính của hormone tăng trưởng tiểu tuyến và hormone tăng trưởng của tuyến giáp. Hai hormone này đóng vai trò quan trọng trong sự tăng trưởng và phát triển của cơ thể, bao gồm cả chiều cao. Việc thiếu iốt có thể gây ra rối loạn tuyến giáp và gây ảnh hưởng đến sự phát triển chiều cao.

Kẽm (Zn): Kẽm là một chất dinh dưỡng quan trọng tham gia vào quá trình phát triển cơ bắp và xương. Nó được tìm thấy trong nhiều loại thực phẩm như thịt, hải sản, hạt, và đậu. Sự thiếu hụt kẽm có thể ảnh hưởng đến sự phát triển và tăng trưởng của cơ thể, bao gồm cả chiều cao.

Magie (Mg): Magie là một nguyên tố quan trọng tham gia vào hơn 300 quá trình sinh học trong cơ thể con người, bao gồm cả sự phát triển và tăng trưởng. Nó có vai trò trong quá trình hình thành xương, chức năng cơ bắp và quá trình truyền tín hiệu thần kinh. Thiếu hụt magie có thể ảnh hưởng đến tăng trưởng và phát triển chiều cao.

(x - 13 + y)² + (x - 6 - y)² ≥ 0 + 0 = 0

Vì dấu "=" xảy ra nên x - 13 + y = 0 và x - 6 - y = 0

x + y = 13 và x - y = 6

x = (13 - 6) : 2 = 3,5

y = 13 - 3,5 = 9,5

Vậy x = 3,5 và y = 9,5

(\(x\) - 13 + y)² + (\(x\) - 6 - y)² = 0

(\(x\) - 13 + y)² ≥ 0 ∀ \(x;y\)

(\(x-6-y\))² ≥ 0 ∀ \(x;y\)

⇒(\(x-13+y\))² + (\(x\) - 6- y)² = 0

⇔ \(\left\{{}\begin{matrix}x-13+y=0\\x-6-y=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x-6-y=0\\x-13+y+x-6-y=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}y=x-6\\2x=19\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{19}{2}-6\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{7}{2}\end{matrix}\right.\)

|5 - \(\dfrac{2}{3}\)\(x\)| + |\(\dfrac{2}{3}\)y - 4| =0

|5 - \(\dfrac{2}{3}\)\(x\)| ≥ 0 ∀ \(x\); |\(\dfrac{2}{3}\)y - 4| ≥ 0 ∀ y

⇒ |5 - \(\dfrac{2}{3}\)\(x\)| + |\(\dfrac{2}{3}\)y - 4| = 0 ⇔ \(\left\{{}\begin{matrix}5-\dfrac{2}{3}x=0\\\dfrac{2}{3}y-4=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{15}{2}\\y=6\end{matrix}\right.\)

\(\dfrac{5}{6}\) - (\(\dfrac{3}{4}\) + \(\dfrac{7}{8}\) - \(x\)) = 10 - | \(\dfrac{1}{3}\) - \(\dfrac{1}{2}\)|

\(\dfrac{5}{6}\) - (\(\dfrac{13}{8}\)- \(x\)) = 10 - |-\(\dfrac{1}{6}\)|

 \(\dfrac{5}{6}\) - \(\dfrac{13}{8}\) + \(x\) = 10 + \(\dfrac{1}{6}\)

- \(\dfrac{19}{24}\) + \(x\)      = \(\dfrac{61}{6}\)

            \(x\)     = \(\dfrac{61}{6}\) + \(\dfrac{19}{24}\)

            \(x\)     = \(\dfrac{263}{24}\) 

a) 3/13 - 3/2 + 10/13

= (3/13 + 10/13) - 3/2

= 1 - 3/2

= -1/2

b) 4/7 - (-2/7) - 7/3

= 4/7 + 2/7 - 7/3

= 6/7 - 7/3

= -31/21

c) 2/3 - (-1/6) + 5/4

= 2/3 + 1/6 + 5/4

= 8/12 + 2/12 + 15/12

= 25/12

a, 3/13 - 3/2 + 10/13

= 3/13 + 10/13

= 1 - 3/2 = -1/2

b,4/7 - (-2/7) - 7/3

= 4/7 + 2/7 - 7/3

= 6/7 - 7/3

= 18/21 - 14/21

= 4/21

c, 2/3 - -1/6 +5/4 

= 2/3 + 1/16 +5/4

= 128/192 + 12/192 + 240/192

= 380/192

= 95/4 

không hiểu chỗ nào hỏi tui

Hình vẽ nào vậy em

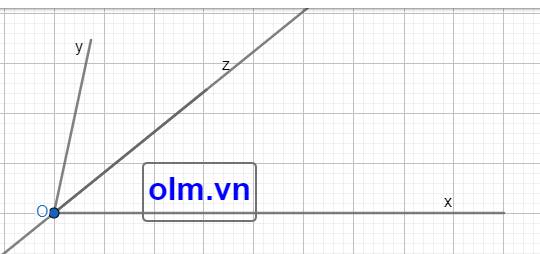
a, Trên cùng một nửa mặt phẳng có bờ là tia ox vì \(\widehat{xOy}\) > \(\widehat{xOz}\) nên Oz nằm giữa hai tia Oy và Ox.

b, \(\widehat{xOy}\) = \(\widehat{xOz}\) +  \(\widehat{zOy}\) ⇒ \(\widehat{zOy}\)  = 80⁰ -  40⁰ = 40⁰

c, Oz nằm giữa hai tia Oy và Ox và \(\widehat{zOy}\) = \(\widehat{xOz}\)  nên OZ là tia phân giác của góc xOy