Ta thấy \(a=1000^{1001}\) 

\(=1000.1000^{1000}\) 

\(=1000^{1000}+1000^{1000}+...+1000^{1000}\) (1000 lần)

\(>1^1+2^2+...+1000^{1000}\)

 Nên \(a>c\)

 Lại có \(2^{2^{64}}=2^{2^4.2^{60}}=\left(2^{2^4}\right)^{2^{60}}\) \(>\left(2^{10}\right)^{2^{10}}=1024^{1024}>1000^{1001}\) nên \(b>a\)

 Vậy \(b>a>c\)

Giá trị nhỏ nhất của P là 1 =)))

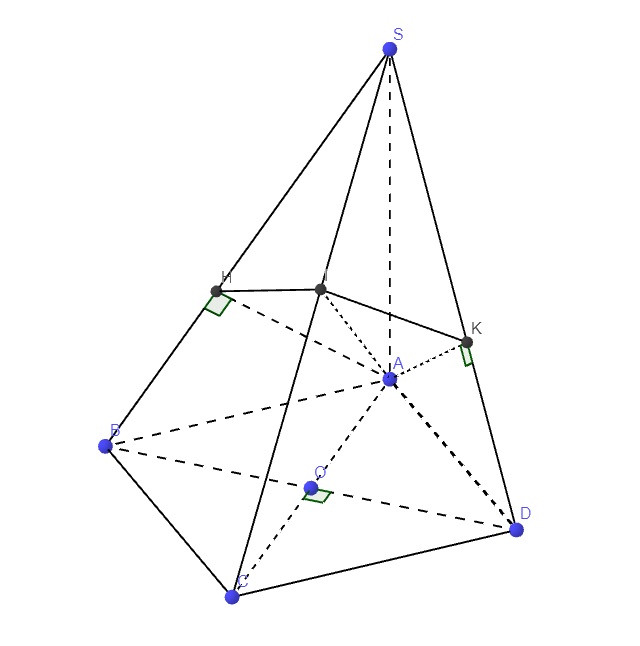
a.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)

b.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{ hai đường chéo hình vuông}\right)\end{matrix}\right.\)

\(\Rightarrow BD\perp\left(SAC\right)\)

Mà (SAC) đi qua trung điểm O của BD

\(\Rightarrow\left(SAC\right)\) là mp trung trực của BD

c.

Theo câu a ta có: \(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\\AH\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow BC\perp AH\)

Mà \(AH\perp SB\left(gt\right)\)

\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)

Lại có \(AI\perp SC\left(gt\right)\)

\(\Rightarrow SC\perp\left(AIH\right)\) (1)

Tương tự, ta chứng minh được \(AK\perp\left(SCD\right)\Rightarrow AK\perp SC\)

\(\Rightarrow SC\perp\left(AIK\right)\) (2)

(1);(2) \(\Rightarrow\left(AIH\right)\) trùng \(\left(AIK\right)\) hay 3 đường AH, AI, AK cùng nằm trong 1 mp

 TH1: Nếu con gà chạy sang chuồng 2 là một con gà mái thì lúc này chuồng 2 có 7 con gà trống và 4 con gà mái \(\Rightarrow\) P(gà trống) \(=\dfrac{7}{11}\)

 TH2: Nếu con gà chạy sang chuồng 2 là một con gà trống thì lúc này chuồng 2 có 8 con gà trống và 3 con gà mái \(\Rightarrow\) P(gà trống) \(=\dfrac{8}{11}\)

 Bởi chuồng 1 có số lượng gà trống và gà mái bằng nhau nên xác suất để 1 con gà trống hay 1 con gà mái chạy từ chuồng 1 sang chuồng 2 là như nhau.

 \(\Rightarrow\) P(gà trống) \(=\dfrac{\dfrac{7}{11}+\dfrac{8}{11}}{2}=\dfrac{15}{22}\)

2) Bạn bổ sung thêm đề bài nhé.