Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D = \(\dfrac{1}{2.7}\) + \(\dfrac{1}{7.12}\) + \(\dfrac{1}{12.17}\) + ... + \(\dfrac{1}{37.42}\)
D = \(\dfrac{5}{5}\).(\(\dfrac{1}{2.7}\) + \(\dfrac{1}{7.12}\)+ \(\dfrac{1}{12.17}\)+...+ \(\dfrac{1}{37.42}\))
D = \(\dfrac{1}{5}\).\(\left(\dfrac{5}{2.7}+\dfrac{5}{7.12}+\dfrac{5}{12.17}+...+\dfrac{5}{37.42}\right)\)
D = \(\dfrac{1}{5}\).(\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{12}\) + \(\dfrac{1}{12}\) - \(\dfrac{1}{17}\) + ... + \(\dfrac{1}{37}\) - \(\dfrac{1}{42}\))
D = \(\dfrac{1}{5}\).( \(\dfrac{1}{2}\) - \(\dfrac{1}{42}\))
D = \(\dfrac{1}{5}\) . \(\dfrac{10}{21}\)
D = \(\dfrac{2}{21}\)
\(D=\dfrac{1}{2.7}+\dfrac{1}{7.12}+\dfrac{1}{12.17}+...+\dfrac{1}{37.42}\)
\(=\dfrac{1}{5}.\left(\dfrac{7-2}{2.7}+\dfrac{12-7}{7.12}+\dfrac{17-12}{12.17}+...+\dfrac{42-37}{37.42}\right)\)
\(=\dfrac{1}{5}.\left(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{17}+...+\dfrac{1}{37}-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{5}.\left(\dfrac{1}{2}-\dfrac{1}{42}\right)\)
\(=\dfrac{1}{5}.\dfrac{10}{21}\)
\(=\dfrac{2}{21}\)


1 giờ 30 phút = 1,5 giờ
2 giờ 20 phút = \(\dfrac{7}{3}\) giờ
Quãng đường người đó đi với vận tốc 15,5 km/giờ:
\(15,5\times1,5=23,25\left(km\right)\)
Quãng đường người đó đi với vận tốc 12 km/giờ:
\(12\times\dfrac{7}{3}=28\left(km\right)\)
Quãng đường từ Đà Nẵng đến Mỹ Sơn dài:
\(23,25+28=51,25\left(km\right)\)
Đổi đơn vị:
1 giờ 30 phút = 1,5 giờ
2 giờ 20 phút = 2,33 giờ
Quãng đường đi được trong 1,5 giờ đầu:
Quãng đường = Vận tốc x Thời gian
Quãng đường = 15,5km/giờ x 1,5 giờ
Quãng đường = 23,25km
Quãng đường đi được trong 2,33 giờ tiếp theo:
Quãng đường = Vận tốc x Thời gian
Quãng đường = 12km/giờ x 2,33 giờ
Quãng đường = 27,96km
Quãng đường từ Đà Nẵng đến Mỹ Sơn:
Quãng đường = Quãng đường đi được trong 1,5 giờ đầu + Quãng đường đi được trong 2,33 giờ tiếp theo
Quãng đường = 23,25km + 27,96km
Quãng đường = 51,21km

\(\dfrac{2^{19}.27^3+15.4^9.9^4}{9^4.4^{10}.12^{10}}\)
\(=\dfrac{2^{19}.\left(3^3\right)^3+3.5.\left(2^2\right)^9.\left(3^2\right)^4}{\left(3^2\right)^4.\left(2^2\right)^{10}.\left(2^2.3\right)^{10}}\)
\(=\dfrac{2^{19}.3^9+3.5.2^{18}.3^8}{3^8.2^{20}.2^{20}.3^{10}}\)
\(=\dfrac{2^{19}.3^9+3^9.5.2^{18}}{3^{18}.2^{40}}\)
\(=\dfrac{2^{18}.3^9.\left(2+5\right)}{3^{18}.2^{40}}\)
\(=\dfrac{7}{3^9.2^{22}}\)
2 19 . 2 7 3 + 15. 4 9 . 9 4 9 4 . 4 10 + 1 2 10 9 4 .4 10 +12 10
2 19 .27 3 +15.4 9 .9 42 19 .( 2 7 3 + 27 3 ) + 15.4 9 .( 9 4 9 4 + 9 4 ) + 1 2 10 9 4 .4 10 +12 10
= 2 19 .100 + 15.4 9 . 94 + 1 2 10 9 4 .4 10 +12 10
= 2000 + 1410 + 1 2 10 9 4 .4 10 +12 10
= 2000 + 1410 + 2 10 9 + 12 10
= 2000+1412+123424

Quy đổi đơn vị:
1 giờ = 60 phút = 3600 giây
Giải:
Gọi vận tốc của người thứ nhất là x km/h (x > 0).
Khi đó, vân tốc của người thứ hai là x + 14 km/h.
Thời gian người thứ nhất đi từ A đến B là: 8 giờ - 6 giờ = 2 giờ.
Thời gian người thứ hai đi từ A đến B là: 11 giờ - 8 giờ = 3 giờ.
Quãng đường từ A đến B là:
- Người thứ nhất: 2x km
- Người thứ hai: 3(x + 14) km
Vì quãng đường từ A đến B là như nhau nên ta có phương trình:
2x = 3(x + 14)
Giải phương trình:
2x = 3x + 42 => x = 42
Vậy vận tốc của người thứ nhất là 42 km/h, vận tốc của người thứ hai là 42 + 14 = 56 km/h.

Tính hợp lý:
2 19 . 2 7 3 + 15. 4 9 . 9 4 9 4 . 4 10 + 1 2 10 9 4 .4 10 +12 10 2 19 .27 3 +15.4 9 = (2 19 . 2 7 3 +15. 4 9 ) + (9 4 9 4 . 4 10 +1 2 10 9 4 .4 10 ) + (12 10 +2 19 .27 3 ) = 10 + 40 + 1 = 51Chứng minh định lý:
Kẻ AH vuông góc với BC.
Ta có:
-
ΔADE và ΔADH có:
- Góc ADE = Góc ADH (= 90 độ)
- AD chung
- Góc DAE = Góc HAD (cùng phụ với góc EAD) => ΔADE ~ ΔADH (g-g) => DE/DH = AD/AE (1)
-
ΔCDG và ΔCDH có:
- Góc CDG = Góc CDH (= 90 độ)
- CD chung
- Góc DGC = Góc HDG (cùng phụ với góc CDG) => ΔCDG ~ ΔCDH (g-g) => DG/DH = CD/CE (2)
Nhân (1) và (2), ta được:
DE/DH . DG/DH = AD/AE . CD/CE => DE . DG = AD . CD
Vậy DB . DC = DE . DG (đpcm)

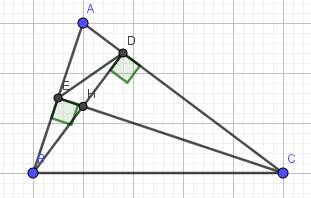
a) Xét hai tam giác vuông: \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABD\) ∽ \(\Delta ACE\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\)
\(\Rightarrow AE.AB=AD.AC\)
b) Do \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\) có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(cmt\right)\)
\(\widehat{A}\) chung
\(\Rightarrow\Delta ADE\) ∽ \(\Delta ABC\left(g-g\right)\)
\(\Rightarrow\widehat{ADE}=\widehat{ABC}\)