Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

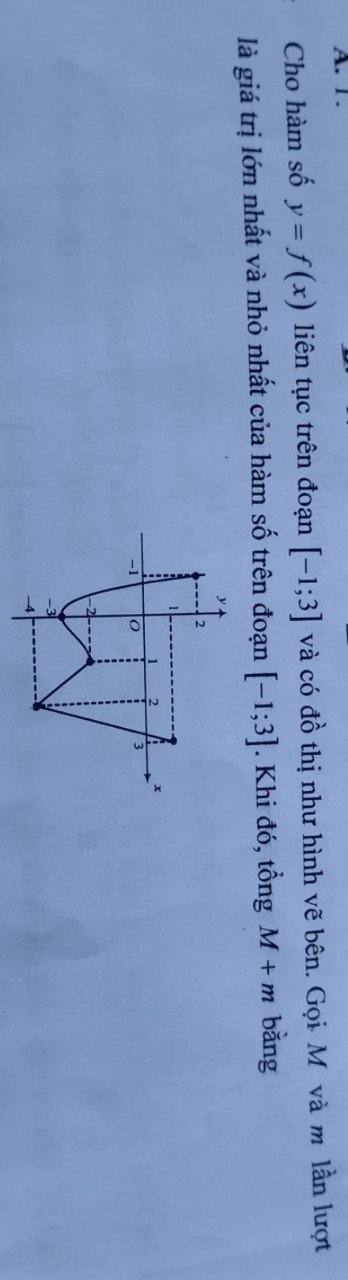
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)
và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)
Khi đó \(M+m=2-4=-2\)

Có \(y'=x^2-2mx-1\)
Xét pt \(y'=x^2-2mx-1=0\)(*), có \(\Delta'=m^2+1>0\) nên (*) luôn có 2 nghiệm phân biệt \(x_1,x_2\)
Theo định lý Viète, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
Để \(x_1^2+x_2^2=2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=2\)
\(\Leftrightarrow\left(2m\right)^2+2=2\)
\(\Leftrightarrow4m^2=0\)
\(\Leftrightarrow m=0\)
Vậy \(m=0\) thỏa mãn ycbt.

a, A''Có đúng 2 nữ''
\(C^2_3.C_{56}^2\)
\(P\left(A\right)=\dfrac{C_3^2.C_{56}^2}{C_{59}^4}\)
b, B''Có ít nhất 2 nam''
TH1 : Có 2 nam \(C_{56}^2.C_3^2\)
TH2 : Có 3 nam \(C_{56}^3.C_3^1\)
TH3 : Có 4 nam \(C^4_{56}\)
\(\Rightarrow C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4\)
\(P\left(B\right)=\dfrac{C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4}{C_{59}^4}\)
c, C''Có nhiều nhất 2 nam''
TH1 : Có 1 nam \(C_{56}^1.C_3^3\)
TH2 : Có 2 nam \(C_{56}^2.C_3^2\)
\(\Rightarrow C_{56}^2.C_3^3+C_{56}^2.C_3^2\)
\(P\left(C\right)=\dfrac{C_{56}^2.C_3^3+C^2_{56}.C_3^2}{C_{59}^4}\)

Lấy điểm A bất kì nằm trên đường tròn đáy.
Khi đó góc tạo bởi đường sinh và mặt phẳng đáy chính là \(\widehat{SAO}=45^o\)
Do đó \(h=r=\dfrac{a}{\sqrt{2}}\)
\(\Rightarrow S_{xq}=\pi rl=\pi.\dfrac{a}{\sqrt{2}}.a=\dfrac{\pi a^2}{\sqrt{2}}\)
\(S_{tp}=S_{xq}+\pi r^2=\dfrac{\pi a^2}{\sqrt{2}}+\pi\left(\dfrac{a}{\sqrt{2}}\right)^2=\dfrac{\pi a^2\sqrt{2}+\pi a^2}{2}\)

1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)
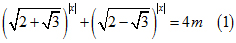 với m là tham số.
với m là tham số.