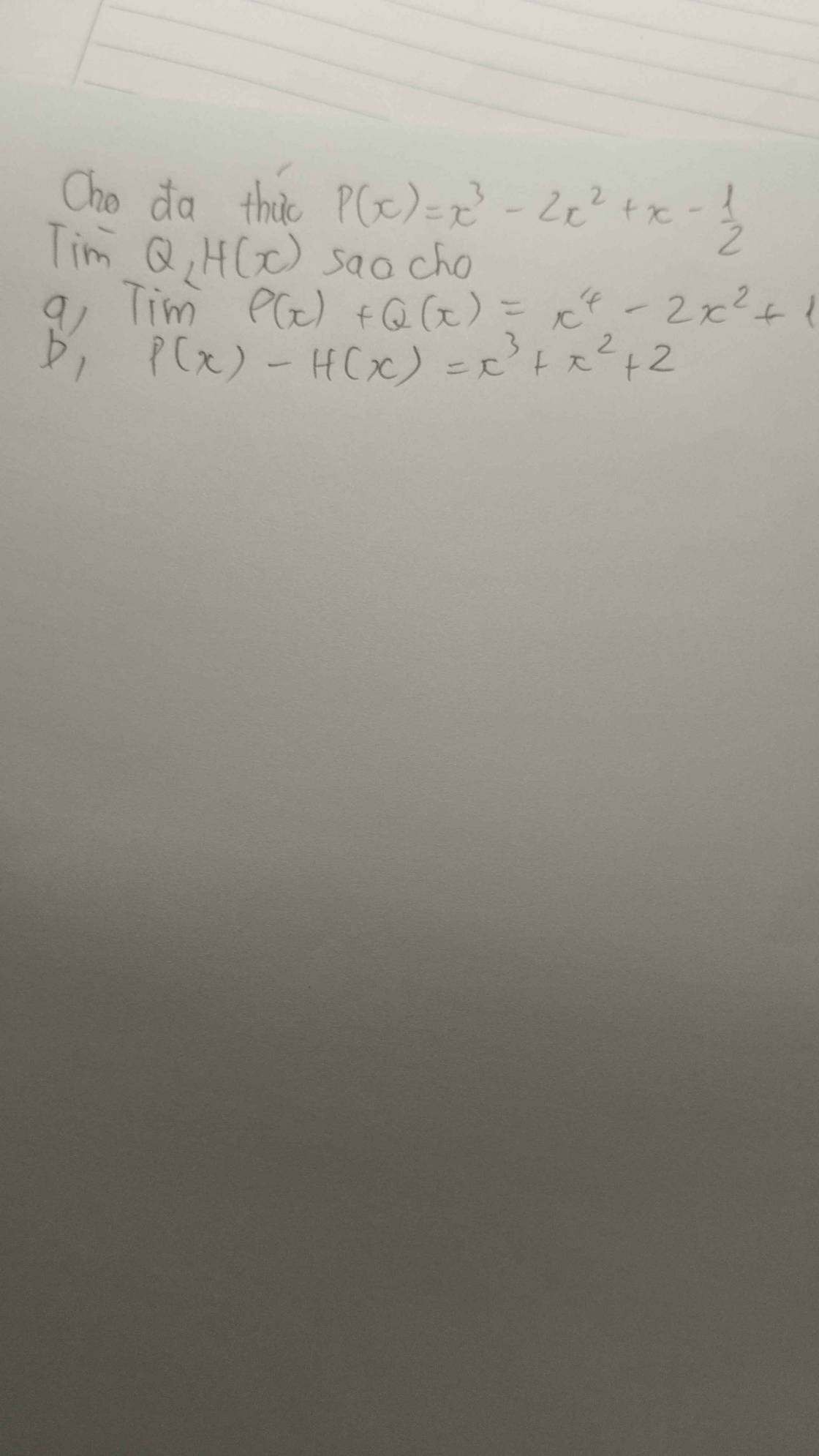
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d=ƯCLN(n-2;n-1)
=>\(\left\{{}\begin{matrix}n-2⋮d\\n-1⋮d\end{matrix}\right.\)
=>\(n-2-n+1⋮d\)
=>\(-1⋮d\)
=>d=1
=>ƯCLN(n-2;n-1)=1
=>\(M=\dfrac{n-2}{n-1}\) là phân số tối giản

Đặt K(x)=0
=>\(4\left(x+3\right)-x\left(x+1\right)-12=0\)
=>\(4x+12-x^2-x-12=0\)
=>\(-x^2+3x=0\)
=>\(-x\left(x-3\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

a: 5,4:0,027=5400:27
b: \(\left(-17,01\right):\left(-12,15\right)=1701:1215\)
c: \(\left(-15,175\right):12,14=-15175:12140\)

a: \(\dfrac{x^2+5x}{x}=\dfrac{x^2}{x}+\dfrac{5x}{x}=x+5\)
b: \(\dfrac{6x^3-4x^2}{2x^2}=\dfrac{6x^3}{2x^2}-\dfrac{4x^2}{2x^2}=3x-2\)
c: \(\dfrac{8x^2y+6xy}{2xy}=\dfrac{8x^2y}{2xy}+\dfrac{6xy}{2xy}=4x+3\)
d: \(\left(x^2-x+3\right)\left(x-2\right)\)
\(=x^3-2x^2-x^2+2x+3x-6\)
\(=x^3-3x^2+5x-6\)
e: \(\dfrac{8x^3y}{4xy}=\dfrac{8}{4}\cdot\dfrac{x^3}{x}\cdot\dfrac{y}{y}=2x^2\)
f: \(\left(-4xy^2\right)\cdot\left(-\dfrac{1}{4}x\right)=\left(-4\right)\cdot\left(-\dfrac{1}{4}\right)\cdot x\cdot x\cdot y^2=x^2y^2\)
g: \(\dfrac{x^4-2x^2+1}{x-1}\)
\(=\dfrac{\left(x^2-1\right)^2}{x-1}=\dfrac{\left[\left(x-1\right)\left(x+1\right)\right]^2}{\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2\cdot\left(x+1\right)^2}{\left(x-1\right)}=\left(x-1\right)\left(x+1\right)^2\)
Lời giải:
a. $(x^2+5x):x=x(x+5):x=x+5$
b. $(6x^4-4x^2):(2x^2)=2x^2(3x^2-2):(2x^2)=3x^2-2$
c. $(8x^2y+6xy):(2xy)=2xy(4x+3):(2xy)=4x+3$
d.
$(x^2-x+3)(x-2)=x(x^2-x+3)-2(x^2-x+3)$
$=x^3-x^2+3x-2x^2+2x-6=x^3-3x^2+5x-6$
e.
$(8x^3y):(4xy)=2x^2$
f.
$(-4xy^2).\frac{-1}{4}x=x^2y^2$
g.
$(x^4-2x^2+1):(x-1)=(x^2-1)^2:(x-1)=(x-1)^2(x+1)^2:(x-1)=(x-1)(x+1)^2$

A × 1/3 + A × 2/3 + A × 2 - 150 = 450
A × (1/3 + 2/3 + 2) - 150 = 450
A × 3 - 150 = 450
A × 3 = 450 + 150
A × 3 = 600
A = 600 : 3
A = 200
A x \(\dfrac{1}{3}\) + A x \(\dfrac{2}{3}\) + A x 2 - 150 = 450
A x (\(\dfrac{1}{3}\) + \(\dfrac{2}{3}\) + 2) - 150 = 450
A x 3 - 150 = 450
A x 3 = 450 + 150
A x 3 = 600
A = 600 : 3
A = 200

a: 5,4:0,027=5400:27
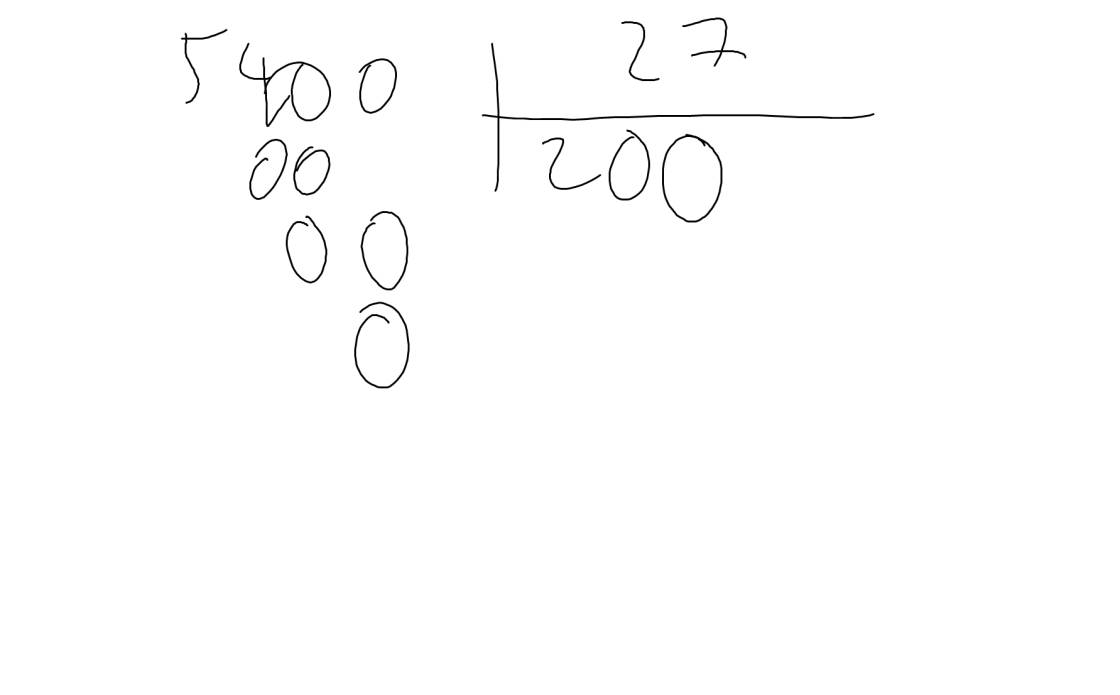
b: (-17,01):(-12,15)=1701:1215
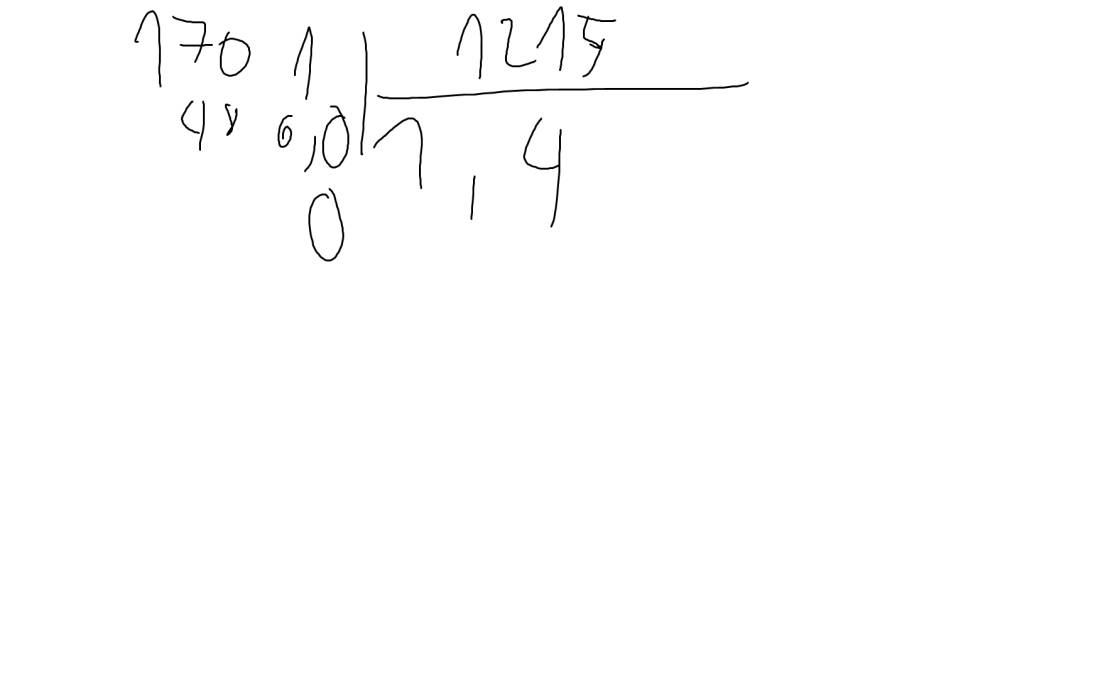
c: (-15,175):12,14=-15175:12140
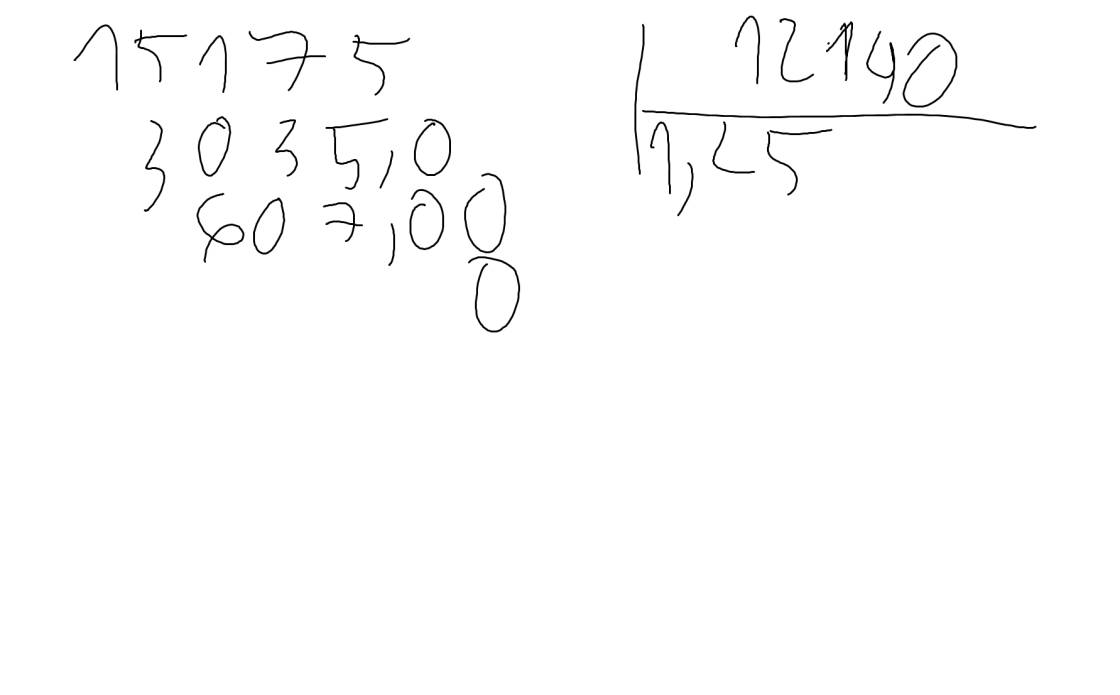

A=1.21+3.41+5.61+...+49.501
𝐴=(1+13+15+...+149)−(12+14+...+150)A=(1+31+51+...+491)−(21+41+...+501)
𝐴=(1+12+13+14+15+16+...+149+150)−2(12+14+...+150)A=(1+21+31+41+51+61+...+491+501)−2(21+41+...+501)
𝐴=(1+12+13+14+15+16+...+149+150)−(1+12+13+...+125)A=(1+21+31+41+51+61+...+491+501)−(1+21+31+...+251)
𝐴=126+127+...+149+150<126+126+126+...+126=2526<1.A=261+271+...+491+501<261+261+261+...+261=2625<1.
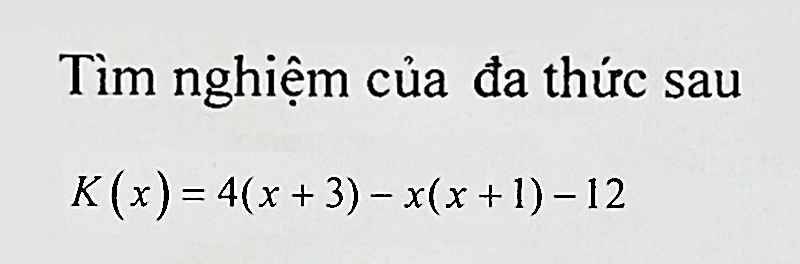
a) \(P\left(x\right)+Q\left(x\right)=x^4-2x^2+1\)
\(\Rightarrow Q\left(x\right)=x^4-2x^2+1-P\left(x\right)\)
\(=x^4-2x^2+1-\left(x^3-2x^2+x-\dfrac{1}{2}\right)\)
\(=x^4-2x^2+1-x^3+2x^2-x+\dfrac{1}{2}\)
\(=x^4-x^3+\left(-2x^2+2x^2\right)-x+\left(1+\dfrac{1}{2}\right)\)
\(=x^4-x^3-x+\dfrac{3}{2}\)
b) \(P\left(x\right)-H\left(x\right)=x^3+x^2+2\)
\(\Rightarrow H\left(x\right)=P\left(x\right)-\left(x^3+x^2+2\right)\)
\(=\left(x^3-2x^2+x-\dfrac{1}{2}\right)-\left(x^3+x^2+2\right)\)
\(=x^3-2x^2+x-\dfrac{1}{2}-x^3-x^2-2\)
\(=\left(x^3-x^3\right)+\left(-2x^2-x^2\right)+x+\left(-\dfrac{1}{2}-2\right)\)
\(=-3x^2+x-\dfrac{5}{2}\)