Bài 15. Cho hình thang ABCD có đáy nhỏ bằng AB bằng 10,8 cm. Đáy lớn DC
bằng 27 cm. Nối A với C. Tính diện tích tam giác ADC, biết diện tích tam giác
ABC là 54 cm2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau 30p=0,5 giờ, xe máy đi được: \(36\times0,5=18\left(km\right)\)
Thời gian để ô tô đuổi kịp xe máy là:
8h57p-7h45p=1h12p=1,2(giờ)
Hiệu vận tốc của ô tô và xe máy là:
18:1,2=15(km/h)
Vận tốc của ô tô là:
15+36=51(km/h)

Ta có :
abc9 + abc = 1395
abc x 10 + 9 + abc = 34362
abc x 11 = 34362 - 9
abc x 11 = 34353
abc = 34353:11
abc = 3123
Giải:
Vì xóa chữ số 9 ở hàng đơn vị của số thứ nhất ta được số thứ hai và tổng hai số là 34362 nên số thứ nhất là số có 5 chữ số, bằng 10 lần số thứ hai và 9 đơn vị.
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số bé là: 34362 - 9):(10 + 1) x 1 = 3123
Số lớn là: 3123 x 10 + 9 = 31239
Đáp số: 31239

\(S_{ABCD}=\dfrac{1}{2}\left(AD+BC\right)\cdot12=6\cdot\left(20+10\right)=180\left(cm^2\right)\)
Vì AD//BC
nên \(\dfrac{AD}{BC}=\dfrac{MA}{MC}=\dfrac{MD}{MB}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\dfrac{S_{DAB}}{S_{DBC}}=\dfrac{AD}{BC}=\dfrac{10}{20}=\dfrac{1}{2}\)
mà \(S_{DAB}+S_{DBC}=S_{ABCD}=180\left(cm^2\right)\)
nên \(S_{DAB}=180\cdot\dfrac{1}{3}=60\left(cm^2\right);S_{DBC}=180-60=120\left(cm^2\right)\)
Vì MD/MB=1/2 nên \(S_{ADM}=\dfrac{1}{2}\cdot S_{AMB}\)
mà \(S_{ADM}+S_{AMB}=S_{ABD}=60\left(cm^2\right)\)
nên \(S_{ADM}=\dfrac{1}{3}\cdot60=20\left(cm^2\right);S_{AMB}=60-20=40\left(cm^2\right)\)
Vì AM=1/2MC nên \(S_{AMB}=\dfrac{1}{2}\cdot S_{BMC}\)
=>\(S_{BMC}=2\cdot S_{AMB}=80\left(cm^2\right)\)
\(S_{AMD}+S_{AMB}+S_{MDC}+S_{MBC}=S_{ABCD}\)
=>\(20+40+80+S_{DMC}=180\)
=>\(S_{DMC}=180-80-60=40\left(cm^{\&2}\right)\)
Ta có:
S MDA/S MAB = DK/BH (2 tam giác có chung đáy AM)
Mà DK/BH = S ACD/S ABC (2 tam giác có chung đáy AC)
Lại có:S ACD/S ABC = AD/BC(2 tam giác có chiều cao hạ từ A và C bằng nhau)
==>S MDA/S MAB=AD/BC=20/10=2(cm)
Mà S MAD+S MAB=S ABD=20x12:2=120(cm2)
Vậy theo cách tìm dạng toán tìm hai số biết tổng(60cm2) và tỉ số(2),ta có:
S MAB=120:(2+1)=40 (cm2)
Lại thấy: S ABC=10x12:2=60 (cm2)
S ACD=20x12:2=120 (cm2)
S MBC=S ABC - S MAB=60-40=20 (cm2)
Nên S MCD=S ACD-SMAD=120-(60+20)=40 (cm2)
Đáp số:S MAB=40cm2;S MBC=20cm2;S MCD=40cm2

Bài 10:
Giờ thứ hai đi được: \(\dfrac{2}{5}+\dfrac{1}{7}=\dfrac{14+5}{35}=\dfrac{19}{35}\)(quãng đường)
Sau hai giờ thì phần quãng đường còn lại là:
\(1-\dfrac{2}{5}-\dfrac{19}{35}=\dfrac{3}{5}-\dfrac{19}{35}=\dfrac{2}{35}\)(quãng đường)
Bài 9:
a: \(\dfrac{7}{8}-\dfrac{5}{16}+\dfrac{1}{2}=\dfrac{14}{16}-\dfrac{5}{16}+\dfrac{8}{16}=\dfrac{17}{16}\)
b: \(\dfrac{7}{5}+\dfrac{4}{5}-\dfrac{3}{7}=\dfrac{11}{5}-\dfrac{3}{7}=\dfrac{77-15}{35}=\dfrac{62}{35}\)
Bài 2:D
Bài 3:C
Bài 4: C

\(x^2\ge y^2+z^2\Rightarrow\dfrac{x^2}{y^2+z^2}\ge1\)
\(P=\dfrac{y^2+z^2}{x^2}+x^2\left(\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)+2019\ge\dfrac{y^2+z^2}{x^2}+x^2.\dfrac{4}{y^2+z^2}+2019\)
\(P\ge\dfrac{y^2+z^2}{x^2}+\dfrac{x^2}{y^2+z^2}+3\dfrac{x^2}{y^2+z^2}+2019\)
\(P\ge2\sqrt{\dfrac{y^2+z^2}{x^2}.\dfrac{x^2}{y^2+z^2}}+3.1+2019=2024\)
\(P_{min}=2024\) khi \(x^2=2y^2=2z^2\)

\(\dfrac{13}{60}+\dfrac{18}{30}+\dfrac{11}{60}=\dfrac{13+11}{60}+\dfrac{18}{30}\)
\(=\dfrac{24}{60}+\dfrac{36}{60}=\dfrac{60}{60}=1\)
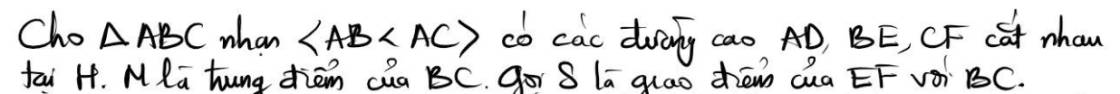

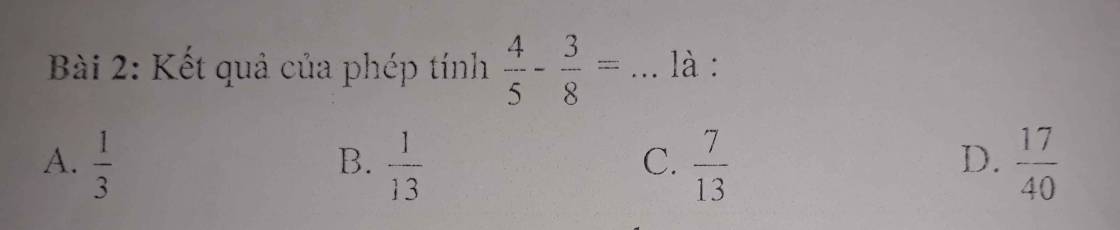

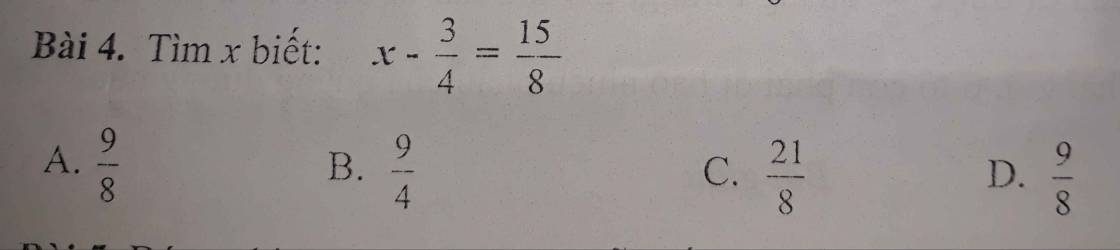



Kẻ CH\(\perp\)AB; AK\(\perp\)DC
Ta có: CH\(\perp\)AB
AB//DC
Do đó: CH\(\perp\)DC
mà AK\(\perp\)DC
=>CH//AK
Xét tứ giác AKCH có
AK//CH
AH//CK
Do đó: AKCH là hình bình hành
=>AK=CH(1)
Xét ΔABC có CH là đường cao
nên \(S_{CAB}=\dfrac{1}{2}\times CH\times AB\left(2\right)\)
Xét ΔCAD có AK là đường cao
nên \(S_{ADC}=\dfrac{1}{2}\times AK\times DC\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{S_{CAB}}{S_{DAC}}=\dfrac{AB}{DC}=\dfrac{2}{5}\)
=>\(S_{DAC}=S_{CAB}\times\dfrac{5}{2}=54\times\dfrac{5}{2}=135\left(cm^2\right)\)
Chiều cao của tam giác ADC là : 54x2:10.8=10(cm)
Diện tích tam giác ADC là : 27x10:2= 135(cm)