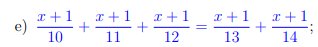Cho n số x1, x2, ..., xn mỗi số nhận giá trị 1 hoặc -1. Chứng minh rằng nếu x1.x2 + x2.x3 + ...+ xn.x1 = 0 thì n chia hết cho 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a)\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\\ \left(\dfrac{-2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\\ \left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\dfrac{\left(-7\right)^2}{4^2}=\dfrac{49}{16}\\ \left(-0,1\right)^4=\left(-\dfrac{1}{10}\right)^4=\dfrac{\left(-1\right)^4}{10^4}=\dfrac{1}{10000}\)
\(b)\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\\ \dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\\ \dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1^2}{5^2}=\dfrac{1}{25}\\ \dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-\left(n-1\right)}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)\)

Bài 15:
a: Ta có: \(\widehat{A_1}=\widehat{M_1}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MN
b: ta có: \(\widehat{NMC}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MN//CD
Bài 14:
a: Ta có: \(\widehat{H_1}=\widehat{xAH}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Hm//Ax
b: Ta có: \(\widehat{A_1}=\widehat{K_1}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Ax//Kn

\(a)\left(\dfrac{6}{7}+1\dfrac{1}{2}\right)^2\\ =\left(\dfrac{6}{7}+\dfrac{3}{2}\right)^2\\ =\left(\dfrac{12}{14}+\dfrac{21}{14}\right)^2\\ =\left(\dfrac{33}{14}\right)^2\\ =\dfrac{1089}{196}\\ b)\left(2\dfrac{1}{5}-1\dfrac{2}{3}\right)^3\\ =\left(\dfrac{11}{5}-\dfrac{5}{3}\right)^3\\ =\left(\dfrac{33}{15}-\dfrac{25}{15}\right)^3\\ =\left(\dfrac{8}{15}\right)^3\\ =\dfrac{512}{3375}\\ c)3^2+4\cdot\left(\dfrac{7}{9}\right)^0+\left[\left(-5\right)^2:\dfrac{1}{5}\right]:25\\ =9+4\cdot1+\left(5^2\cdot5\right):25\\ =13+5^3:5^2\\ =13+5\\ =18\)

\(a)64^x:16^x=256\\ \Rightarrow\left(2^6\right)^x:\left(2^4\right)^x=256\\ \Rightarrow2^{6x}:2^{4x}=256\\ \Rightarrow2^{6x-4x}=2^8\\ \Rightarrow2^{2x}=2^8\\ \Rightarrow2x=8\\ \Rightarrow x=\dfrac{8}{2}=4\\ b)\dfrac{-2401}{7^x}=-7\\ \Rightarrow7^x=\dfrac{-2401}{-7}\\ \Rightarrow7^x=343\\ \Rightarrow7^x=7^3\\ \Rightarrow x=3\\ c)\dfrac{625}{\left(-5\right)^x}=25\\ \Rightarrow\left(-5\right)^x=\dfrac{625}{25}\\ \Rightarrow\left(-5\right)^x=25\\ \Rightarrow\left(-5\right)^x=\left(-5\right)^2\\ \Rightarrow x=2\)

Lời giải:
\(B=\frac{-3}{4}.\frac{-8}{9}.\frac{-15}{16}....\frac{-99}{100}\\
=-\frac{3.8.15...99}{4.9...100}\) (do $B$ có lẻ các thừa số)
\(=-\frac{(1.3)(2.4)(3.5)...(9.11)}{2^2.3^2.4^2...10^2}\)
\(=-\frac{(1.2.3...9)(3.4.5...11)}{(2.3....10)(2.3.4...10)}\\ =-\frac{1.2.3...9}{2.3.4...10}.\frac{3.4.5...11}{2.3.4...10}\\ =-\frac{1}{10}.\frac{11}{2}=\frac{-11}{20}< \frac{-11}{21}\)

b: \(\dfrac{2}{5}-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(-\dfrac{1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{2}{5}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\left(\dfrac{2}{5}-\dfrac{4}{5}+\dfrac{2}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{9}+\dfrac{11}{9}\right)\)
\(=-\dfrac{4}{3}+\dfrac{12}{9}=0\)
c: \(\dfrac{11}{8}\cdot\left[\left(-\dfrac{5}{11}:\dfrac{13}{8}-\dfrac{5}{11}:\dfrac{13}{5}\right)+\dfrac{-6}{33}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\cdot\dfrac{8}{13}-\dfrac{5}{11}\cdot\dfrac{5}{13}+\dfrac{-2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\left(\dfrac{8}{13}+\dfrac{5}{13}\right)-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\dfrac{-7}{11}+\dfrac{3}{4}=-\dfrac{7}{8}+\dfrac{3}{4}=-\dfrac{1}{8}\)

e: \(\dfrac{x+1}{10}+\dfrac{x+1}{11}+\dfrac{x+1}{12}=\dfrac{x+1}{13}+\dfrac{x+1}{14}\)
=>\(\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)=\left(x+1\right)\left(\dfrac{1}{13}+\dfrac{1}{14}\right)\)
=>\(\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
=>x+1=0
=>x=-1

Bài 6:
\(a)P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{33\cdot37}+\dfrac{2}{37\cdot41}\\ =\dfrac{1}{2}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{33\cdot37}+\dfrac{4}{37\cdot41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{33}-\dfrac{1}{37}+\dfrac{1}{37}-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{41}\right)\\ =\dfrac{1}{2}\cdot\dfrac{40}{41}\\ =\dfrac{20}{41}\\ b)Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\\ =\dfrac{6}{7}\cdot\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\left(\dfrac{1}{2}-\dfrac{1}{121}\right)\\ =\dfrac{6}{7}\cdot\dfrac{119}{242}\\ =\dfrac{51}{121}\)
Bài 5:
a: Để A>0 thì \(\dfrac{2a-1}{-5}>0\)
=>2a-1<0
=>\(a< \dfrac{1}{2}\)
b: Để A<0 thì \(\dfrac{2a-1}{-5}< 0\)
=>2a-1>0
=>2a>1
=>\(a>\dfrac{1}{2}\)
c: Để A=0 thì \(\dfrac{2a-1}{-5}=0\)
=>2a-1=0
=>2a=1
=>\(a=\dfrac{1}{2}\)
Bài 6:
a: \(P=\dfrac{2}{1\cdot5}+\dfrac{2}{5\cdot9}+...+\dfrac{2}{37\cdot41}\)
\(=\dfrac{2}{4}\cdot\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{37\cdot41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{37}-\dfrac{1}{41}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{41}\right)=\dfrac{1}{2}\cdot\dfrac{40}{41}=\dfrac{20}{41}\)
b: \(Q=\dfrac{6}{2\cdot9}+\dfrac{6}{9\cdot16}+...+\dfrac{6}{114\cdot121}\)
\(=\dfrac{6}{7}\left(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{7}{114\cdot121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{114}-\dfrac{1}{121}\right)\)
\(=\dfrac{6}{7}\left(\dfrac{1}{2}-\dfrac{1}{121}\right)=\dfrac{6}{7}\cdot\dfrac{119}{242}=\dfrac{51}{121}\)

a: \(-\dfrac{25}{20}< 0;0< \dfrac{20}{25}\)
Do đó: \(-\dfrac{20}{25}< \dfrac{20}{25}\)
b: \(\dfrac{15}{21}=\dfrac{15:3}{21:3}=\dfrac{5}{7};\dfrac{21}{49}=\dfrac{21:7}{49:7}=\dfrac{3}{7}\)
mà 5>3
nên \(\dfrac{15}{21}>\dfrac{21}{49}\)
c: \(\dfrac{-19}{49}=\dfrac{-19\cdot47}{49\cdot47}=\dfrac{-893}{49\cdot47}\)
\(\dfrac{-23}{47}=\dfrac{-23\cdot49}{47\cdot49}=\dfrac{-1127}{47\cdot49}\)
mà -893>-1127
nên \(-\dfrac{19}{49}>-\dfrac{23}{47}\)


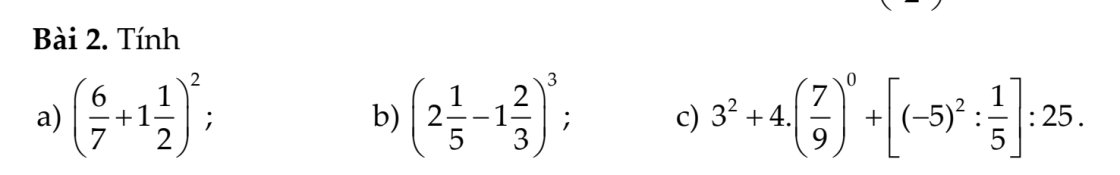
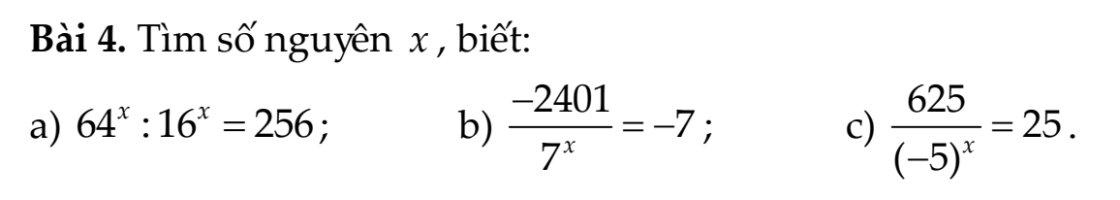
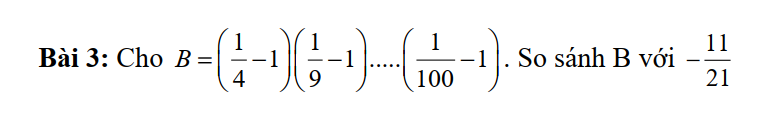
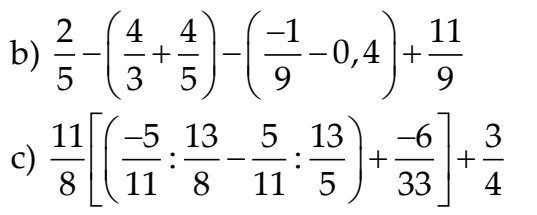 HELP ME. SOS!!!
HELP ME. SOS!!!