cho tam giác abc nhọn, không cân (ab< ac), các đường cao ad,be,cf cắt nhau tại trực tâm h . gọi m,i lần lượt là trung điểm của bc, ah. đường thẳng qua i vuông góc với am, cắt ef tại s. 1) chứng minh ie vuông góc với me. 2) chứng minh sa song song với bc. 3) gọi p,q lần lượt là giao điểm của si với be,cf.chứng minh i là trung điểm của pq.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{4ab}{a+2b}+\dfrac{9ca}{a+4c}+\dfrac{4bc}{b+c}\)
\(P=\dfrac{4abc}{ac+2bc}+\dfrac{9abc}{ab+4bc}+\dfrac{4abc}{ab+ac}\)
\(P=abc\left(\dfrac{4}{ac+2bc}+\dfrac{9}{ab+4bc}+\dfrac{4}{ab+ac}\right)\)
\(P\ge abc.\dfrac{\left(2+3+2\right)^2}{ac+2bc+ab+4bc+ab+ac}\)
\(P\ge abc.\dfrac{49}{2ab+6bc+2ca}\)
\(P\ge abc.\dfrac{49}{7abc}\) (vì \(2ab+6bc+2ca=7abc\))
\(P\ge7\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{ac+2bc}=\dfrac{3}{ab+4bc}=\dfrac{2}{ab+ac}\\2ab+6bc+2ca=7abc\end{matrix}\right.\)
\(\dfrac{2}{ac+2bc}=\dfrac{2}{ab+ac}\) \(\Leftrightarrow2b=a\)
Có \(\dfrac{3}{ab+4bc}=\dfrac{2}{ab+ac}\)
\(\Leftrightarrow\dfrac{3}{2b^2+4bc}=\dfrac{2}{2b^2+2bc}\)
\(\Leftrightarrow3b^2+3bc=2b^2+4bc\)
\(\Leftrightarrow b^2=bc\Leftrightarrow b=c\)
\(\Rightarrow a=2b=2c\)
Lại có \(2ab+6bc+2ca=7abc\) \(\Rightarrow4b^2+6b^2+4b^2=14b^3\)
\(\Leftrightarrow b=1\)
\(\Leftrightarrow\left(a,b,c\right)=\left(2,1,1\right)\)
Vậy \(min_P=7\)

Lời giải:
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z}$
$\Rightarrow (\frac{1}{x}+\frac{1}{y})+(\frac{1}{z}-\frac{1}{x+y+z})=0$
$\Leftrightarrow \frac{x+y}{xy}+\frac{x+y}{z(x+y+z)}=0$
$\Leftrightarrow (x+y)(\frac{1}{xy}+\frac{1}{z(x+y+z)})=0$
$\Leftrightarrow (x+y).\frac{z(x+y+z)+xy}{xyz(x+y+z)}=0$
$\Leftrightarrow (x+y).\frac{(z+x)(z+y)}{xyz(x+y+z)}=0$
$\Leftrightarrow (x+y)(y+z)(x+z)=0$
$\Leftrightarrow x=-y$ hoặc $y=-z$ hoặc $z=-x$
Nếu $x=-y$ thì:
$P=\frac{3}{4}+[(-y)^8-y^8](y^9+z^9)(z^{10}-x^{10})=\frac{3}{4}+0.(y^9+z^9)(z^{10}-x^{10})=\frac{3}{4}$
Nếu $y=-z$ thì:
$P=\frac{3}{4}+(x^8-y^8)[(-z)^9+z^9](z^{10}-x^{10})=\frac{3}{4}+(x^8-y^8).0.(z^{10}-x^{10})=\frac{3}{4}$
Nếu $z=-x$ thì:
$P=\frac{3}{4}+(x^8-y^8)(y^9+z^9)[(-x)^{10}-x^{10}]=\frac{3}{4}+(x^8-y^8)(y^9+z^9).0=\frac{3}{4}$

Ảnh bé và mờ quá. Bạn nên gõ hẳn đề lên để mọi người hỗ trợ tốt hơn nhé.

Lời giải:
a.
Khi $x=1$ thì: $A=\frac{1}{\sqrt{1}+4}=\frac{1}{1+4}=\frac{1}{5}$
b. \(B=\frac{2(\sqrt{x}+3)-(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{12}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{\sqrt{x}+9}{(\sqrt{x}-3)(\sqrt{x}+3)}-\frac{12}{(\sqrt{x}-3)(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}+9-12}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}=\frac{1}{\sqrt{x}+3}\)
Ta có đpcm.
c. Với mọi $x\geq 0$ và $x\neq 9$ thì: $\sqrt{x}\geq 0\Rightarrow \sqrt{x}+3\geq 3$
$\Rightarrow B=\frac{1}{\sqrt{x}+3}\leq \frac{1}{3}< \frac{1}{2}$
Ta có đpcm.

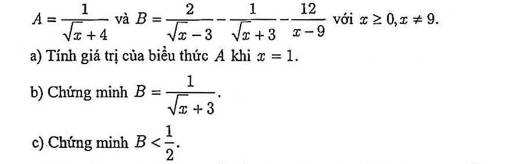
\({}\)

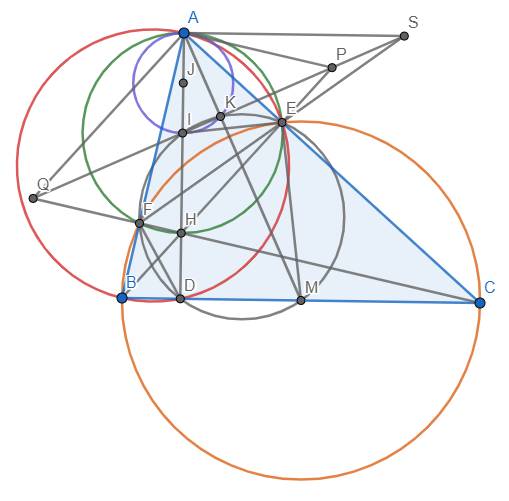
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)