:0

a, Xét tam giác MKN và tam giác MKO có

MK chung

MN = MO ( cmt)

\(\widehat{NMK}=\widehat{OMK}\) ( do MK là tia phân giác )

=> tam giác MKN = tam giác MKO (c-g-c)

b, Do tam giác MKN = tam giác MKO (cmt)  

=> KN = KO 

c, Do MK là trung điểm NO 

mà MK cách đều hai điểm N và O 

=> MK là đường trung trực

=> MK vuông góc với NO

4dm=cm

a) Xét ΔBMC và ΔCNB có :

          BM=CN ( AB=AC; AM=AN )

          góc B = góc C ( ΔABC cân tại A )

         BC : chung

suy ra : hai Δ trên bằng nhau theo trường hợp ( c-g-c )

suy ra : đpcm

b) chứng minh EBC cân nha em

Từ : ΔBMC = ΔCNB

suy ra : góc MCB = góc NBC ( 2 góc tương ứng )

suy ra : đpcm

c) ta có : ΔABC cân tại A

suy ra : góc B = góc C= \(\dfrac{180-A}{2}\) (1)

ta lại có : ΔAMN cân tại A 

suy ra : góc AMN = góc ANM = \(\dfrac{180-A}{2}\) (2)

Từ (1) và (2) suy ra đpcm do (các góc ở vị trí đồng vị và bằng nhau )

a) Xét ΔBAD và ΔBED vuông lần lượt tại A và E có : 

                    BD : cạnh chung 

                    góc ABD = góc EBD ( DB là tia phân giác của góc B )

Do đó : ΔBAD=ΔBED ( c.h-g.n )

suy ra : BA = BE ( 2 cạnh tương ứng )

b) Ta có : BA = BE ( cmt )

                DA = DE ( ΔBAD=ΔBED )

suy ra : BD là đường trung trực của AE

suy ra : BD vuông góc với AE (1)

Xét ΔBFD và ΔBCD vuông tại F và E có :

                góc B : chung

                BE=BA (cmt)

do đó : ΔBFD=ΔBCD ( c.g.v-g.n.k )

suy ra : BC = BF

Xét ΔBDF và ΔBDC có :

              BC=BF ( cmt )

             góc FBD = góc CBD ( BD là tia phân giác của góc B )

             BD : chung 

do đó : hai tam giác trên bằng nhau theo trường hơp ( c-g-c )

suy ra : DF=DC ( 2 cạnh tương ứng )

ta có : DF=DC ; BC=BF

suy ra : BD là đường trung trực của CF

suy ra : BD vuông CF (2)

Từ (1) và (2) suy ra : đpcm

a) Xét tam giác ABD và EBD có
góc BAD=BED=90⁰(gt)
góc ABD=EBD(BD là phân giác)
BD chung
=>tam giác ABD = tam giác EBD( cạnh huyền -  góc nhọn )
=>BA=BE( 2 cạnh tương ứng )
b)Có BA=BE => tam giác BAE cân tại B
mà BD là tia phần giác góc B => BD là đường cao => BD vuông góc AE
Có tam giác ABD = tam giác EBD => AD=ED (2 cạnh tương ứng)
Xét tam giác ADF và EDC có
góc DAF=DEC=90^o(gt)
góc FAD=EDC (2 góc đối đỉnh)
AD=ED (cmt)
=>tam giác ADF = tam giác EDC(cgv-gnk)
=>AF=EC ( 2 cạnh tương ứng)
có BF=AF+AB; BC=CE+EB
mà AF=EC, AB=EB => BF=BC => tam giác FBC cân tại B
mà BD là tia phân giác => BD là đường cao => BD vuông góc CF
mà BD vuông góc với AE
=> AE song song CF

Lấy $E\in AD$ sao cho $AE=AB$ mà $AD=AB+AC$ nên $AC=DE.$

$\Delta ABE$ cân có $\widehat{BAD}={60}^{\circ }$ nên $\Delta ABE$ là tam giác đều suy ra $AE=EB.$

Thấy $\widehat{BED}=\widehat{EBA}+\widehat{EAB}={120}^{\circ }$  (góc ngoài tại đỉnh $E$ của tam giác $ABE$ )  nên $\widehat{BED}=\widehat{BAC}\left(={120}^{\circ }\right)$

Suy ra $\Delta EBD=\Delta ABC\left(c.g.c\right)\Rightarrow \widehat{B_1}=\widehat{B_2}$ (hai góc tương ứng bằng nhau) và $BD=BC$ (hai cạnh tương ứng)

Lại có $\widehat{B_1}+\widehat{B_3}={60}^{\circ }$ nên $\widehat{B_2}+\widehat{B_3}={60}^{\circ }.$

$\Delta BCD$ cân tại $B$ có $\widehat{CBD}={60}^{\circ }$ nên nó là tam giác đều.

Đây nhé!

lười làm lắm

a) Có 81⁷ - 27⁹ + 3²⁹ 

 = (3⁴)⁷ - (3³)⁹ + 3²⁹

= 3²⁸ - 3²⁷ + 3²⁹

= 3²⁷(3 - 1 + 3²)

= 3²⁷.11 = 3²⁶.33 \(⋮33\)

b) 9¹¹ - 9¹⁰ - 9⁹

= 9⁹(9² - 9 - 1) 

= 9⁹.71

= 9⁸.639 \(⋮639\)

c) P = 36³⁶ - 9²⁰⁰⁰ 

Có 36³⁶ = \(\overline{....6}\)

\(9^{2000}=\left(9^2\right)^{1000}=81^{1000}=\overline{.....1}\)

nên P = \(\overline{...6}-\overline{...1}=\overline{...5}\Rightarrow P⋮5\)

dễ thấy P \(⋮9\) mà (5;9) = 1

nên \(P⋮9.5=45\)

A = \(2^2.\left(1^2+2^2+3^2+...+10^2\right)=4.385=1540\)

B=\(3^2.\left(1^2+2^2+3^2+...+10^2\right)=385.9=3465\)

a) \(\dfrac{x}{y}=\dfrac{1}{3}\Rightarrow y=3x\). Thay vào biểu thức N, ta có: \(N=\dfrac{x-3x}{x+9x}=\dfrac{-2x}{10x}=-\dfrac{1}{5}\)

b) \(x+y+1=0\Leftrightarrow x+y=-1\). Thay vào biểu thức M, ta có: \(M=\left(-1\right)^2-y^3\left(-1\right)+x^2-y^3+3\) \(=1+y^3+x^2-y^3+3\) \(=x^2+4\)

`x/(y+z+1)(1)`

`y/(x+z+2)(2)`

`z/(x+y-3)(3)`

Xét TH1 : `x+y+z ne 0`

Áp dụng tính chất dãy tỉ số bằng nhau

`x/(y+z+1)=y/(x+z+2)=z/(x+y-3)=(x+y+z)/(y+z+1+x+z+2+x+y-3)`

`= (x+y+z)/(2x+2y+2z)= 1/2`

`=> x+y+z =1/2`

`=> {(y+z=1/2-x),(x+z=1/2-y),(x+y=1/2-z):}`

Thay `y+z=1/2-x` vào (1) ta giải ra đc 

`x = 1/2`

làm tg tự ta có

`y=5/6 ; z = -5/6`

Xét `TH2:x+y+z =0`

`=> x/(y+z+1)=y/(x+z+2)=z/(x+y-3)=x+y+z =0`

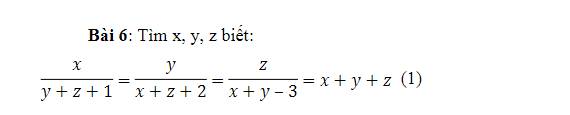
`=> x=y=z =0 `