\(\dfrac{2z-4x}{3}=\dfrac{3x-2y}{4}=\dfrac{4y-3z}{2}\)

\(\Rightarrow\dfrac{6z-12x}{9}=\dfrac{12x-8y}{16}=\dfrac{8y-6z}{4}=\dfrac{6z-12x+12x-8y+8y-6z}{4}=0\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{6z-12x}{9}=0\\\dfrac{12x-8y}{16}=0\\\dfrac{8y-6z}{4}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3z=6x\\6x=4y\\4y=3z\end{matrix}\right.\)

\(\Rightarrow6x=4y=3z\Rightarrow\dfrac{x}{4}=\dfrac{y}{6}=\dfrac{z}{8}\)

\(\Rightarrow\dfrac{x^2}{16}=\dfrac{y^2}{36}=\dfrac{z^2}{64}=\dfrac{y^2+z^2}{36+64}\)

Do \(200< y^2+z^2< 450\Rightarrow\dfrac{200}{36+64}< \dfrac{x^2}{16}< \dfrac{450}{36+64}\)

\(\Rightarrow32< x^2< 72\)

\(\Rightarrow x^2=\left\{36;49;64\right\}\) \(\Rightarrow x=\left\{6;7;8\right\}\)

- Với \(x=6\Rightarrow\dfrac{6}{4}=\dfrac{y}{6}=\dfrac{z}{8}\Rightarrow\left\{{}\begin{matrix}y=9\\z=12\end{matrix}\right.\)

- Với \(x=7\Rightarrow\dfrac{7}{4}=\dfrac{y}{6}=\dfrac{z}{8}\Rightarrow y=\dfrac{21}{2}\notin Z\left(loại\right)\)

- Với \(x=8\Rightarrow\dfrac{8}{4}=\dfrac{y}{6}=\dfrac{z}{8}\Rightarrow\left\{{}\begin{matrix}y=12\\z=16\end{matrix}\right.\)

Vậy có 2 bộ số thỏa mãn: \(\left[{}\begin{matrix}\left(x;y;z\right)=\left(6;9;12\right)\\\left(x;y;z\right)=\left(8;12;16\right)\end{matrix}\right.\)

a: Xét ΔIMH vuông tại H và ΔIEH vuông tại H có

IM=IE

IH chung

Do đó: ΔIMH=ΔIEH

b: ΔIMH=ΔIEH

=>HM=HE

=>H là trung điểm của ME

Xét ΔIME có

IH,MD là các đường trung tuyến

IH cắt MD tại G

Do đó: G là trọng tâm của ΔIME

=>\(MG=\dfrac{2}{3}MD=8\left(cm\right)\)

c: Xét ΔGME có

GH là đường cao

GH là đường trung tuyến

Do đó: ΔGME cân tại G

=>GM=GE

Bạn cần hỏi điều gì?

ΔABC cân tại A

mà AI là đường trung tuyến

nên AI là phân giác của góc BAC

Xét ΔAID vuông tại D và ΔAIE vuông tại E có

AI chung

\(\widehat{IAD}=\widehat{IAE}\)

Do đó: ΔAID=ΔAIE

=>AD=AE

Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

nên DE//BC

Xét ΔABC có DE//BC

nên \(\dfrac{AD}{AB}=\dfrac{DE}{BC}\)

mà AD<AB

nên DE<BC

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>\(a=bk;c=dk\)

\(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\left(k-1\right)}=\dfrac{k+1}{k-1}\)

\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)

Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>\(a=bk;c=dk\)

\(\dfrac{a-b}{2\left(c-d\right)}=\dfrac{bk-b}{2\left(dk-d\right)}=\dfrac{b\left(k-1\right)}{2d\left(k-1\right)}=\dfrac{b}{2d}\)

\(\dfrac{a+b}{2\left(c+d\right)}=\dfrac{bk+b}{2\left(dk+d\right)}=\dfrac{b\left(k+1\right)}{2d\left(k+1\right)}=\dfrac{b}{2d}\)

Do đó: \(\dfrac{a-b}{2\left(c-d\right)}=\dfrac{a+b}{2\left(c+d\right)}\)

a: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

b: Ta có: ΔAIB=ΔAIC

=>\(\widehat{BAI}=\widehat{CAI}\)

Xét ΔADI vuông tại D và ΔAEI vuông tại E có

AI chung

\(\widehat{IAD}=\widehat{IAE}\)

Do đó: ΔADI=ΔAEI

=>AD=AE

Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

nên DE//BC

Xét ΔABC có DE//BC

nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)

mà AD<AB

nên DE<BC

c: Ta có: ΔADI=ΔAEI

=>ID=IE

=>I nằm trên đường trung trực của DE(1)

Ta có: AD=AE
=>A nằm trên đường trung trực của DE(2)

Từ (1),(2) suy ra AI là đường trung trực của DE

a: Xét ΔBAD có BA=BD và \(\widehat{ABD}=60^0\)

nên ΔBAD đều

b: Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)

\(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔDHA vuông tại H)

mà \(\widehat{BAD}=\widehat{BDA}\)

nên \(\widehat{CAD}=\widehat{HAD}\)

Xét ΔAHD vuông tại H và ΔAKD vuông tại K có

AD chung

\(\widehat{HAD}=\widehat{KAD}\)

Do đó: ΔAHD=ΔAKD

=>AH=AK và DH=DK

AH=AK

=>A nằm trên đường trung trực của HK(1)

Ta có: DH=DK

=>D nằm trên đường trung trực của HK(2)

Từ (1),(2) suy ra AD là đường trung trực của HK

c: ΔBAD đều

=>\(\widehat{BAD}=\widehat{BDA}=60^0\); AD=DB=AB

Ta có: \(\widehat{ACB}+\widehat{ABC}=90^0\)

\(\widehat{DAC}+\widehat{DAB}=\widehat{BAC}=90^0\)

mà \(\widehat{ABC}=\widehat{DAB}\left(=60^0\right)\)

nên \(\widehat{DAC}=\widehat{DCA}\)

=>ΔDAC cân tại D

ΔDAC cân tại D

mà DK là đường cao

nên K là trung điểm của AC

Ta có: DA=DC

DA=DB

Do đó: DC=DB

=>D là trung điểm của BC

Xét ΔABC có

AD,BK là các đường trung tuyến

AD cắt BK tại G

Do đó: G là trọng tâm của ΔABC

a: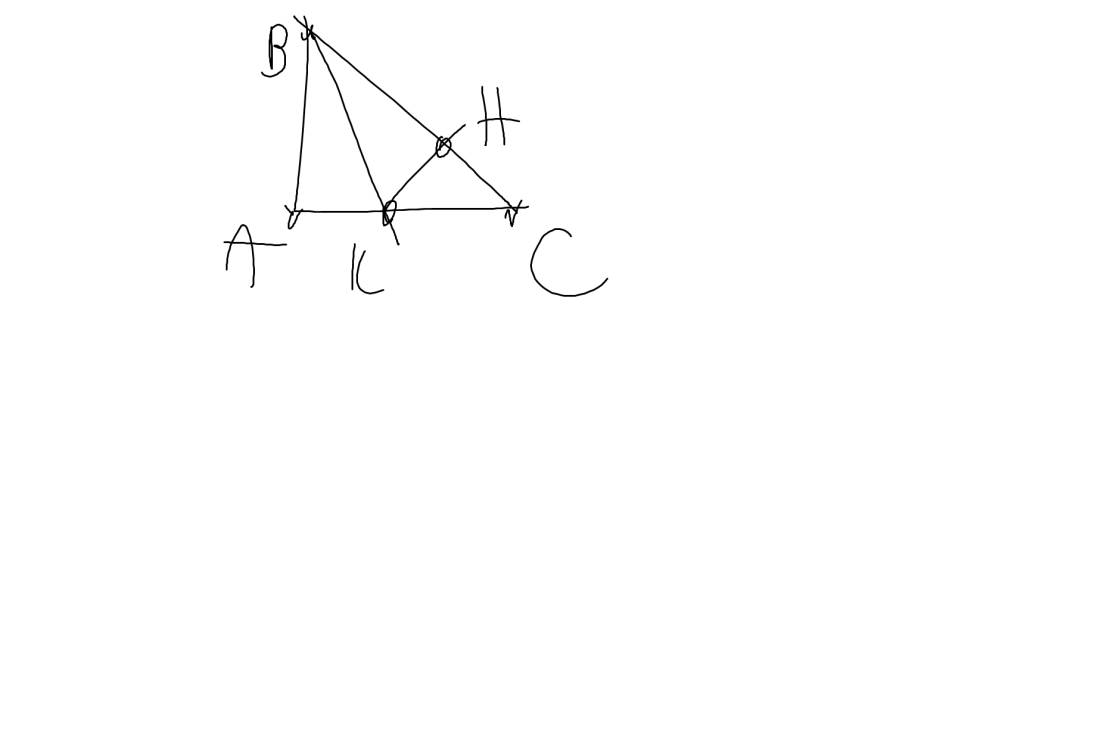 

b: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}+50^0=90^0\)

=>\(\widehat{ACB}=40^0\)

c: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có

BK chung

\(\widehat{ABK}=\widehat{HBK}\)

Do đó: ΔBAK=ΔBHK

d: Ta có: \(\widehat{HKC}+\widehat{C}=90^0\)

=>\(\widehat{HKC}=\widehat{B}=50^0\)

Xét ΔHKC có \(\widehat{HKC}>\widehat{HCK}\)

mà HC,HK lần lượt là cạnh đối diện của các góc HKC,HCK

nên HC>HK

mà HK=AK

nên HC>AK