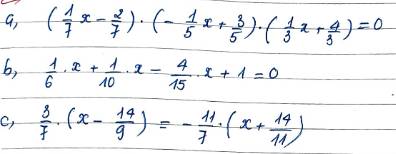
làm ơn giúp tui:((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
Thay x=3 vào phương trình, ta được:
\(\left(3+2\right)\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=3^2-1\)
=>\(5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\left(1\right)\)
Thay x=1/3 vào phương trình, ta được:
\(\left(\dfrac{1}{3}+2\right)\cdot f\left(\dfrac{1}{3}\right)-f\left(3\right)=\left(\dfrac{1}{3}\right)^2-1\)
=>\(\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)-f\left(3\right)=-\dfrac{8}{9}\)
=>\(f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\\f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{35}{3}\cdot f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{56}{3}\\f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{32}{3}\cdot f\left(3\right)=\dfrac{56}{3}-\dfrac{8}{9}=\dfrac{160}{9}\\5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}f\left(3\right)=\dfrac{5}{3}\\f\left(\dfrac{1}{3}\right)=5\cdot\dfrac{5}{3}-8=\dfrac{25}{3}-8=\dfrac{1}{3}\end{matrix}\right.\)
vậy: \(f\left(\dfrac{1}{3}\right)=\dfrac{1}{3}\)

Vì theo bất đẳng thức tam giác "tổng độ dài 2 cạnh luôn lớn hơn cạnh còn lại!
a)3cm,5cm,9cm
Vì 3+5<9
=> a)không thỏa mãn yêu cầu
b)6cm,8cm,10cm
Vì 6+8>10
=> b)thỏa mãn yêu cầu
A B C 6cm 10cm 8cm

\(a,A\left(x\right)+B\left(x\right)=x^3-2x^2+5x-3-x^3+2x^2-3x+5\\ \Rightarrow A\left(x\right)+B\left(x\right)=2x+2.\\ b,A\left(x\right)-B\left(x\right)=x^3-2x^2+5x-3+x^3-2x^2+3x-5\\ \Rightarrow A\left(x\right)-B\left(x\right)=2x^3-4x^2+8x-8.\)

a: \(20p=\dfrac{1}{3}\left(giờ\right)\)
Độ dài quãng đường xe khách đi được sau x giờ là:
\(F\left(x\right)=65x\left(km\right)\)
Độ dài quãng đường xe ô tô đi được sau x-1/3 giờ là:
\(G\left(x\right)=75\left(x-\dfrac{1}{3}\right)\left(km\right)\)
b: \(F\left(2\right)=65\cdot2=130;G\left(2\right)=75\cdot\left(2-\dfrac{1}{3}\right)=150-25=125\)
Vì 130>125
nên độ dài quãng đường xe khách đi được nhiều hơn độ dài quãng đường ô tô đi được 130-125=5km

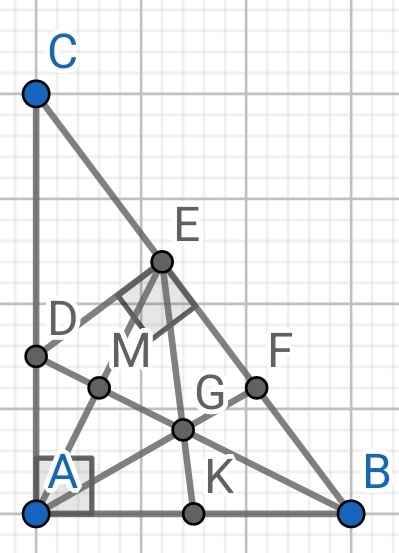
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét hai tam giác vuông: ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AB = EB (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AE
Mà M là giao điểm của BD và AE (gt)
⇒ M là trung điểm của AE
c) Do F là trung điểm của BE (gt)
⇒ BF = BE : 2
Mà BE = AB (cmt)
⇒ BF = AB : 2
Mà BF = BK (gt)
⇒ BK = AB : 2
⇒ K là trung điểm của AB
∆ABE có:
BM là đường trung tuyến (do M là trung điểm của AE)
AF là đường trung tuyến (do F là trung điểm của BE)
Mà G là giao điểm của BM và AF (gt)
⇒ EG là đường trung tuyến thứ ba
Mà K là trung điểm của AB (cmt)
⇒ E, G, K thẳng hàng


a) A(x) = -2x² + x⁴ - 7x + x⁴ + 7
= (x⁴ + x⁴) - 2x² - 7x + 7
= 2x⁴ - 2x² - 7x + 7
B(x) = x⁴ + 2x - 3x⁴ - 6 + 2x² - 4
= (x⁴ - 3x⁴) + 2x² + 2x + (-6 - 4)
= -2x⁴ + 2x² + 2x - 10
b) A(x) + B(x)
= (2x⁴ - 2x² - 7x + 7) + (-2x⁴ + 2x² + 2x - 10)
= 2x⁴ - 2x² - 7x + 7 - 2x⁴ + 2x² + 2x - 10
= (2x⁴ - 2x⁴) + (-2x² + 2x²) + (-7x + 2x) + (7 - 10)
= -5x - 3
A(x) - B(x) = (2x⁴ - 2x² - 7x + 7) - (-2x⁴ + 2x² + 2x - 10)
= 2x⁴ - 2x² - 7x + 7 + 2x⁴ - 2x² - 2x + 10
= (2x⁴ + 2x⁴) + (-2x² - 2x²) + (-7x - 2x) + (7 + 10)
= 4x⁴ - 4x² - 9x + 17
c) C(x) = A(x) + B(x) = -5x - 3
Cho C(x) = 0
-5x - 3 = 0
5x = -3
x = -3/5
Vậy nghiệm của đa thức C(x) là x = -3/5
d) D(x) = C(x).(2x² - 4x + 2)
= (-5x - 3)(2x² - 4x + 2)
= -5x(2x² - 4x + 2) - 3(2x² - 4x + 2)
= -10x³ + 20x² - 10x - 6x² + 12x - 6
= -10x³ + (20x² - 6x²) + (-10x + 12x) - 6
= -10x³ + 14x² + 2x - 6

a: \(\left(\dfrac{1}{7}x-\dfrac{2}{7}\right)\left(-\dfrac{1}{5}x+\dfrac{3}{5}\right)\left(\dfrac{1}{3}x+\dfrac{4}{3}\right)=0\)
=>\(\dfrac{1}{7}\left(x-2\right)\cdot\dfrac{-1}{5}\cdot\left(x-3\right)\cdot\dfrac{1}{3}\left(x+4\right)=0\)
=>(x-2)(x-3)(x+4)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-3=0\\x+4=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=3\\x=-4\end{matrix}\right.\)
b: \(\dfrac{1}{6}x+\dfrac{1}{10}x-\dfrac{4}{15}x+1=0\)
=>\(x\left(\dfrac{1}{6}+\dfrac{1}{10}-\dfrac{4}{15}\right)=1\)
=>\(x\cdot\dfrac{5+3-8}{30}=1\)
=>x*0=1(vô lý)
=>\(x\in\varnothing\)
c: \(\dfrac{3}{7}\left(x-\dfrac{14}{9}\right)=-\dfrac{11}{7}\left(x+\dfrac{14}{11}\right)\)
=>\(\dfrac{3}{7}x-\dfrac{42}{63}=-\dfrac{11}{7}x-\dfrac{14}{7}\)
=>\(2x=-\dfrac{14}{7}+\dfrac{42}{63}=-2+\dfrac{2}{3}=-\dfrac{4}{3}\)
=>\(x=-\dfrac{2}{3}\)