Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2\)
=>\(AB^2-HB^2=AH^2\)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(HA^2=AC^2-HC^2\)
Do đó: \(AC^2-HC^2=AB^2-HB^2\)
=>\(AC^2+HB^2=AB^2+HC^2\)
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{HB}{AB}=\dfrac{BA}{BC}=\dfrac{HA}{AC}\)
=>\(\dfrac{HB}{6}=\dfrac{6}{10}=\dfrac{HA}{8}\)
=>\(HB=6\cdot\dfrac{6}{10}=3,6\left(cm\right);HA=6\cdot\dfrac{8}{10}=4,8\left(cm\right)\)
HB+HC=BC
=>HC+3,6=10
=>HC=6,4(cm)

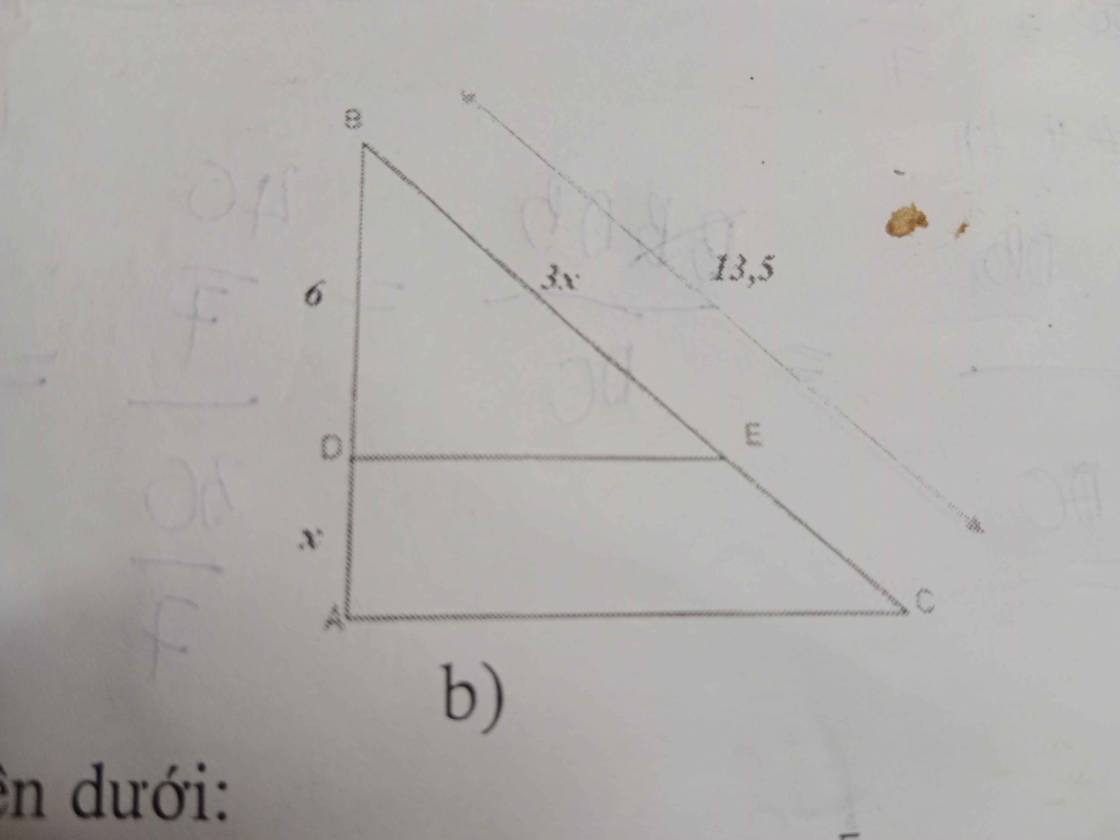
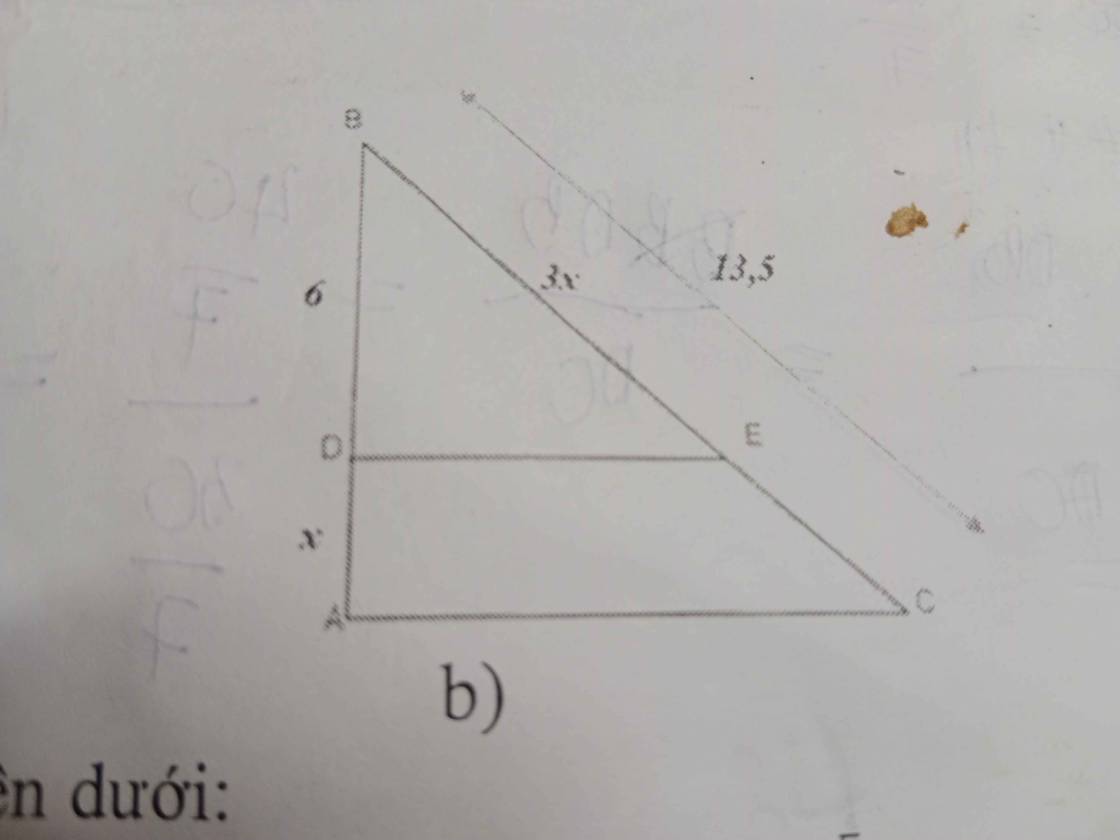
BD+DA=BA
=>BA=6+x
Xét ΔBAC có DE//AC
nên \(\dfrac{BE}{BC}=\dfrac{BD}{BA}\)
=>\(\dfrac{6}{x+6}=\dfrac{3x}{13,5}=\dfrac{x}{4,5}\)
=>\(x\left(x+6\right)=6\cdot4,5=27\)
=>\(x^2+6x-27=0\)
=>(x+9)(x-3)=0
=>\(\left[{}\begin{matrix}x=-9\left(loại\right)\\x=3\left(nhận\right)\end{matrix}\right.\)

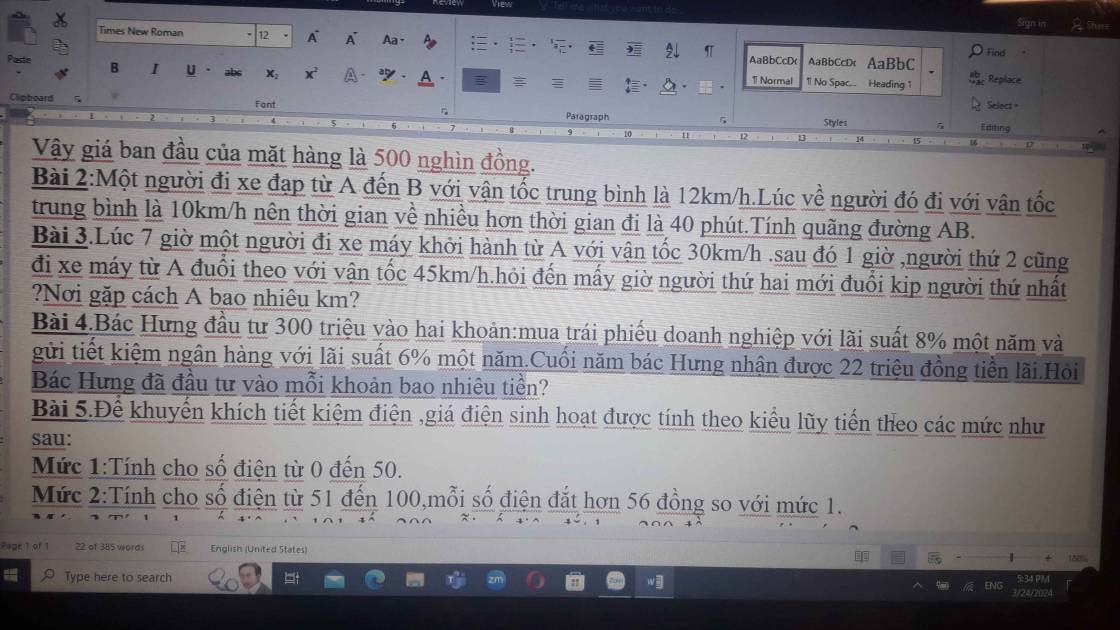
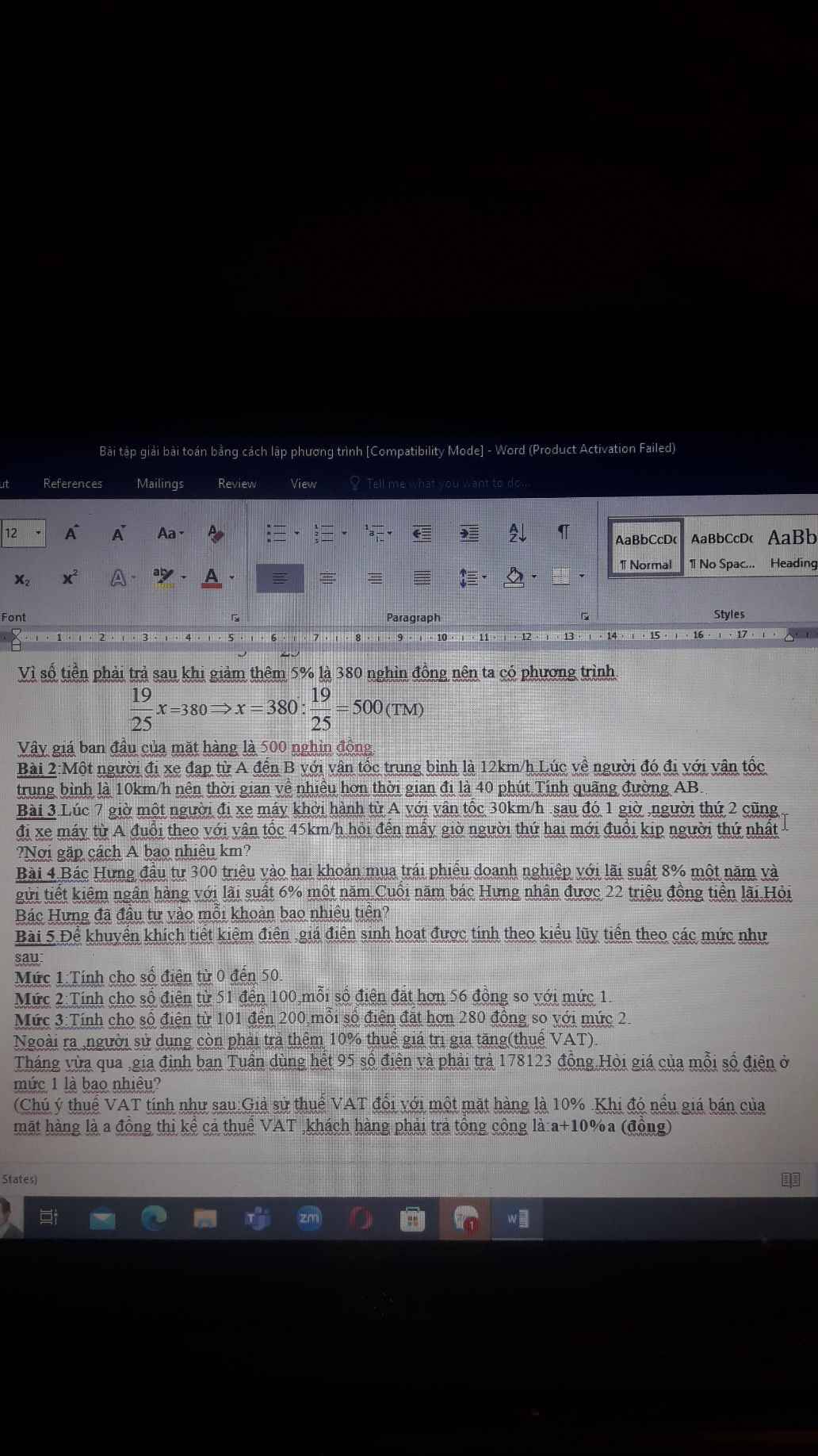
Gọi giá của mỗi số điện ở mức 1 là x(đồng)
(Điều kiện: x>0)
Giá của mỗi số điện ở mức 2 là x+56(đồng)
Số tiền phải trả cho 50 số điện ở mức 1 là 50x(đồng)
Số mức điện dùng ở mức 2 là 95-50=45(số điện)
Số tiền phải trả cho 45 số điện ở mức 2 là \(45\left(x+56\right)\left(đồng\right)\)
Số tiền phải trả(không kể thuế VAT) là:
\(178123\cdot\dfrac{100\%}{110\%}=161930\left(đồng\right)\)
Do đó, ta có phương trình:
\(50x+45\left(x+56\right)=161930\)
=>\(95x+2520=161930\)
=>\(95x=159410\)
=>x=1678(nhận)
Vậy: giá của mỗi số điện ở mức 1 là 1678 đồng

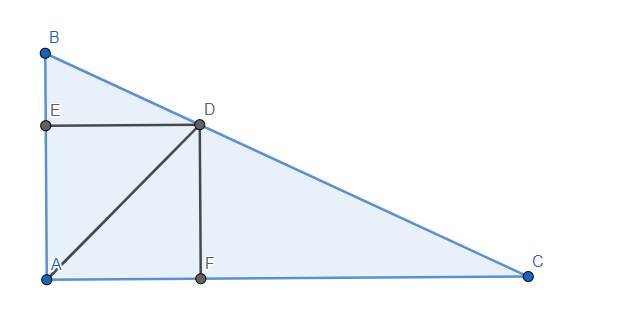
Kẻ DE, DF lần lượt vuông góc với AB, AC tại E, F.
Ta có \(\dfrac{AD^2}{BD^2}=\dfrac{\left(ED\sqrt{2}\right)^2}{BD^2}=\dfrac{2ED^2}{BD^2}=2\left(\dfrac{ED}{BD}\right)^2\) \(=2\left(\dfrac{AC}{BC}\right)^2\)
và \(\dfrac{AD^2}{DC^2}=\dfrac{\left(DF\sqrt{2}\right)^2}{DC^2}=\dfrac{2DF^2}{DC^2}=2\left(\dfrac{DF}{DC}\right)^2=2\left(\dfrac{AB}{BC}\right)^2\)
\(\Rightarrow\dfrac{AD^2}{BD^2}+\dfrac{AD^2}{DC^2}=2\left(\dfrac{AC}{BC}\right)^2+2\left(\dfrac{AB}{BC}\right)^2\) \(=2\left(\dfrac{AB^2+AC^2}{BC^2}\right)\) \(=2\)
\(\Rightarrow\dfrac{1}{BD^2}+\dfrac{1}{CD^2}=\dfrac{2}{AD^2}\), ta có đpcm.
Mình gửi đáp án rồi nhé, bạn vào trang cá nhân của mình xem.

Bài 4:
Gọi số tiền bác Hưng đầu tư cho khoản mua trái phiếu là x(triệu đồng)
(Điều kiện: x>0)
Số tiền bác Hưng đầu tư cho khoản gửi ngân hàng là 300-x(triệu đồng)
Số tiền lãi bác Hưng thu được từ khoản mua trái phiếu là:
8%*x=0,08x(triệu đồng)
Số tiền lãi bác Hưng thu được từ khoản gửi ngân hàng là:
6%*(300-x)=0,06(300-x)(triệu đồng)
Số tiền lãi nhận được là 22 triệu đồng nên ta có:
0,08x+0,06(300-x)=22
=>0,08x+18-0,06x=22
=>0,02x=4
=>x=4:0,02=200(nhận)
Vậy: số tiền bác Hưng đầu tư cho khoản mua trái phiếu là 200 triệu đồng, số tiền bác Hưng đầu tư cho khoản gửi ngân hàng là300-200=100 triệu đồng

Để hai đường thẳng y=5nx-6 và y=4x+6 cắt nhau thì \(5n\ne4\)
=>\(n\ne\dfrac{4}{5}\)
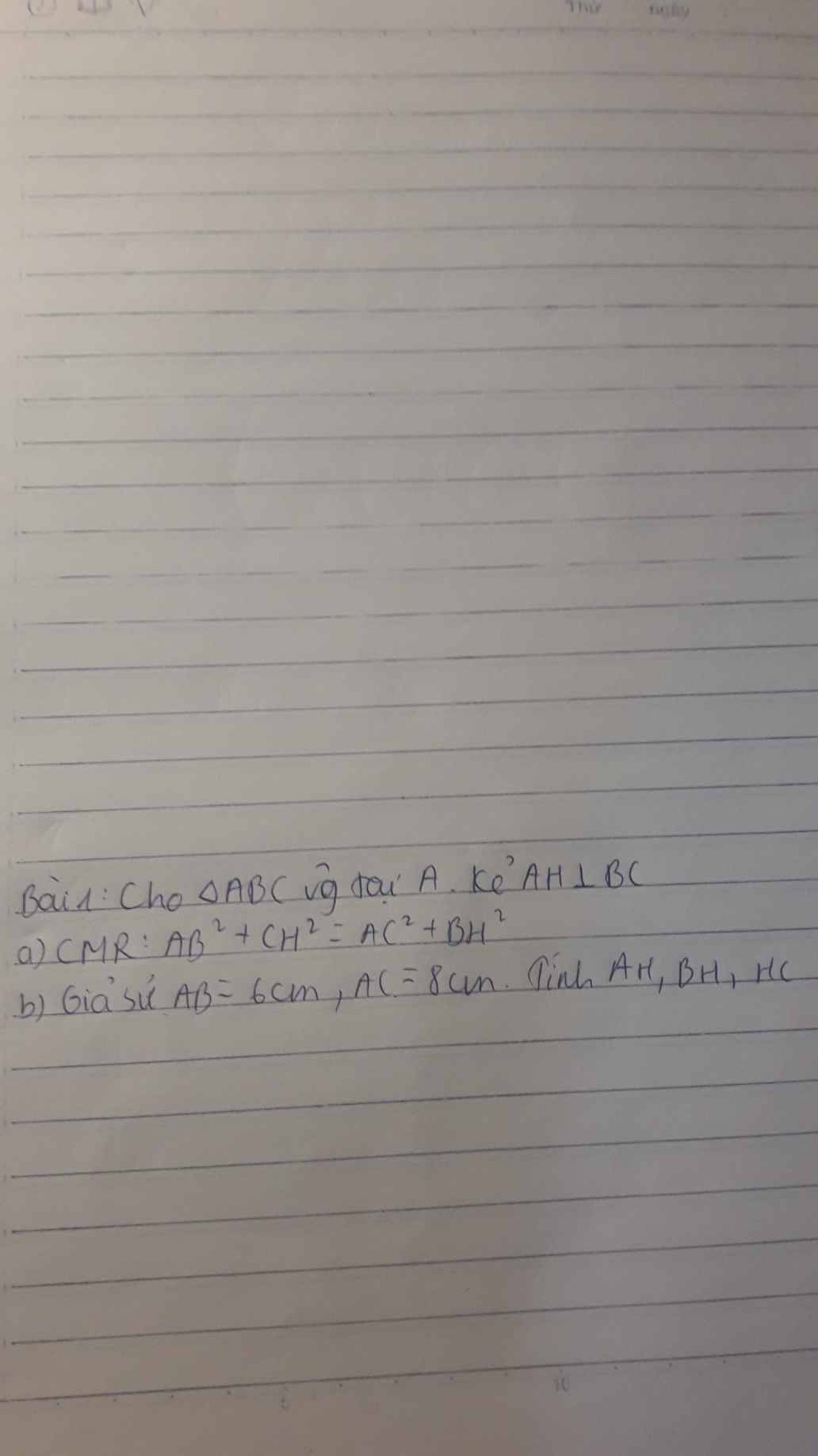



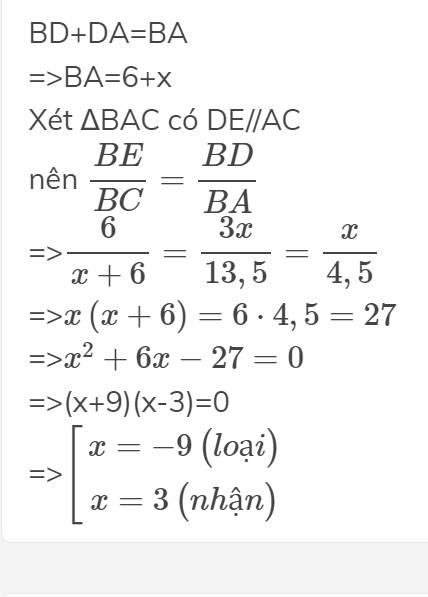

Diện tích đáy là:
\(S=12^2\cdot\dfrac{\sqrt{3}}{4}=36\sqrt{3}\left(cm^2\right)\)
Gọi H là tâm đường tròn ngoại tiếp của ΔABC
=>AH=BH=CH=R
Vì S.ABC là hình chóp tam giác đều
nên SH\(\perp\)(ABC)
Xét ΔABC có \(\dfrac{BC}{sinBAC}=2R\)
=>\(2R=\dfrac{12}{sin60}=12:\dfrac{\sqrt{3}}{2}=12\cdot\dfrac{2}{\sqrt{3}}=8\sqrt{3}\)
=>\(R=4\sqrt{3}\left(cm\right)\)
=>\(AH=BH=CH=4\sqrt{3}\left(cm\right)\)
ΔSHA vuông tại H
=>\(SH^2+HA^2=SA^2\)
=>\(SH^2=8^2-\left(4\sqrt{3}\right)^2=16\)
=>SH=4(cm)
Thể tích hình chóp là:
\(V_{S.ABC}=\dfrac{1}{3}\cdot SH\cdot S_{ABC}=\dfrac{1}{3}\cdot4\cdot36\sqrt{3}=48\sqrt{3}\left(cm^3\right)\)