
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số học sinh lớp 9B là : \(x\) (học sinh) \(\left(x\inℕ^∗\right)\)
\(\Rightarrow\) Số học sinh lớp 9A là : \(x+10\) (học sinh)
Số cây học sinh lớp 9B trồng được : \(4x\) (cây)
Số cây học sinh lớp 9A trồng được : \(3\left(x+10\right)\) (cây)
Vì tổng số cây 2 lớp trồng được là : 275 cây
Nên ta có pt :
\(3\left(x+10\right)+4x=275\\ \Rightarrow3x+30+4x=275\\ \Rightarrow7x=245\\ \Rightarrow x=35\left(TMDK\right)\)
Vậy số HS lớp 9B là : 35 HS và lớp 9A là : 35+10=45(HS)

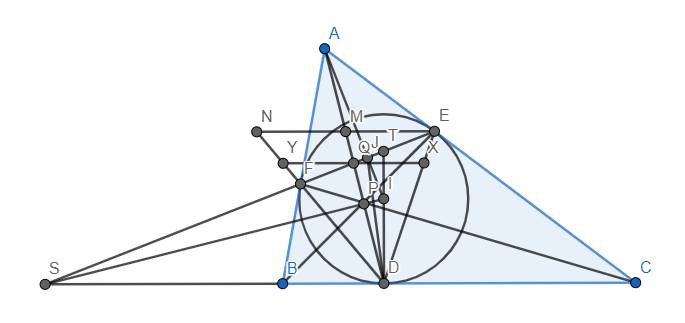
a) Do AE tiếp xúc (I) tại E nên \(\widehat{AEI}=90^o\). Đồng thời dễ dàng chứng minh \(AI\perp EF\) tại J.
Tam giác AEI vuông tại E có đường cao EJ nên \(IJ.IA=IE^2=ID^2=r^2\)
\(\Rightarrow\dfrac{IJ}{ID}=\dfrac{ID}{IA}\). Từ đó dễ có đpcm.
b) Dễ dàng chứng minh tứ giác IDSJ nội tiếp (do có \(\widehat{IJS}=\widehat{IDS}=90^o\)). Do đó \(\widehat{TIJ}=\widehat{TSD}\), dẫn đến \(\Delta TIJ~\Delta TSD\left(g.g\right)\) \(\Rightarrow\dfrac{TI}{TS}=\dfrac{TJ}{TD}\) \(\Rightarrow\) đpcm
Gọi P là giao điểm của AD và IS. Khi đó \(\widehat{PID}=\widehat{SID}=\widehat{SJD}\) và \(\widehat{PDI}=\widehat{ADI}=\widehat{IJD}\) (do đã có \(\Delta IJD~\Delta IDA\) ở câu a))
Do đó \(\widehat{PID}+\widehat{PDI}=\widehat{SJD}+\widehat{IJD}=\widehat{SJI}=90^o\)
\(\Rightarrow\Delta IPD\) vuông tại P, dẫn tới đpcm.
c) Gọi Q là giao điểm của AD và EF. Qua Q kẻ đường thẳng song song với BC cắt DE, DN lần lượt tại X, Y.
Trước hết, ta chứng minh \(\dfrac{EQ}{ES}=\dfrac{FQ}{FS}\) (*)
Ta dễ dàng chứng minh AD, BE, CF đồng quy do định lý Ceva đảo trong tam giác ABC.
\(\Rightarrow\dfrac{QF}{QE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\) (Ceva thuận)
Mặt khác, áp dụng định lý Menelaus cho tam giác AEF với cát tuyến SBC, ta có: \(\dfrac{SF}{SE}.\dfrac{BA}{BF}.\dfrac{CE}{CA}=1\)
Từ đó suy ra \(\dfrac{QF}{QE}=\dfrac{SF}{SE}\Rightarrow\dfrac{EQ}{ES}=\dfrac{FQ}{FS}\) . Vậy (*) được chứng minh.
Áp dụng định lý Thales \(\Rightarrow\dfrac{YQ}{SD}=\dfrac{FQ}{FS};\dfrac{XQ}{SD}=\dfrac{EQ}{ES}\)
Kết hợp với (*), ta có ngay \(YQ=XQ\), từ đó dễ dàng suy ra M là trung điểm NE dựa vào bổ đề hình thang.

A B M N H I K
a/
Ta có
\(AB\perp MN\left(gt\right)\Rightarrow\widehat{MHB}=90^o\)
\(MI\perp BN\Rightarrow\widehat{MIB}=90^o\)
=> H và I cùng nhìn MB dưới 1 góc \(90^o\) => H; I thuộc đường tròn đường kính MB => B; H; M; I cùng thuộc 1 đường tròn
b/
Xét tg vuông MHK và tg vuông MIN có
\(\widehat{MKA}=\widehat{MNI}\) (cùng phụ với \(\widehat{KMN}\) )
Ta có
\(\widehat{MNI}=\widehat{MAK}\) (góc nội tiếp cùng chắn cung MB)
\(\Rightarrow\widehat{MKA}=\widehat{MAK}\) => tg MAK cân tại M
c/
Xét tg vuông MIN và tg vuông MHK có
\(\widehat{MKA}=\widehat{MNI}\) (cmt)
=> tg MNI đồng dạng với MHK (g.g.g)
\(\Rightarrow\dfrac{MI}{MH}=\dfrac{MN}{MK}\)
Ta có tg MAK cân tại M (cmt) => MK=MA
\(\Rightarrow\dfrac{MI}{MH}=\dfrac{MN}{MA}\Rightarrow MI.MA=MH.MN\)

Cảm ơn em đã phản hồi tới olm.vn. Vấn đề em hỏi olm xin trả lời như sau. Hiện tại chính sách olm đã thay đổi. Với mỗi câu trả lời đúng và được giáo viên tick xanh thì chỉ được gp thôi em nhé. Bạn nào đứng top đầu bảng xếp hạng thì cuối tuần sẽ được olm trao xu, xu em có thể đổi quà trên shop của olm. olm đã check câu trả lời của em thì em mới trả lời một câu và cũng chưa được giáo viên nào chấm bài cả em nhé! Nên tất nhiên em chưa thể có xu của olm. Vì xu chỉ trao cho bạn có nhiều gp nhất vào cuối tuần.


Lời giải:
Gọi số lọ sát khuẩn 2 lớp điều chế được ngày thứ nhất lần lượt là $a,b$. Theo bài ra ta có:
$a+b=110$
$1,25a+1,2b=135$
Giải hệ phương trình gồm 2 PT trên thu được: $a=60; b=50$ (lọ)

số tự nhiên bé nhất mà lập phương số đó có 44 chữ số cuối bên phải là chữ số 33 là số: 17
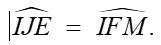
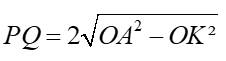
 Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?
Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?
ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)