3xy - 9y ^ 2 + 11y + 2 = 0. x ^ 2 + xy - 6y ^ 2 + 5y - 1 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Toán nâng cao lớp 9, hôm nay olm sẽ hướng dẫn em làm dạng này bằng cách lập phương trình như sau:
Gọi số ngày đội 1 hoàn thành công việc là \(x\) (ngày); \(x>0\)
Trong một ngày đội 1 làm được: 1 : \(x\) = \(\dfrac{1}{x}\) (công việc)
Số ngày đội 1 phải làm một mình là: 16 - 12 = 4 (ngày)
Khi đội 1 tăng năng xuất lên 1,5 lần thì Trong 4 ngày đội 1 hoàn thành được số phần công việc là:
\(\dfrac{1}{x}\) \(\times\) 1,5 \(\times\) 4 = \(\dfrac{6}{x}\) (công việc)
Trong 4 ngày đội 2 làm được: \(\dfrac{6}{x}\) - \(\dfrac{1}{x}\) \(\times\)4 = \(\dfrac{2}{x}\) (công việc)
Trong một ngày đội 2 làm được: \(\dfrac{2}{x}\) : 4 = \(\dfrac{1}{2x}\) (công việc)
Theo bài ra ta có phuong trình:
(\(\dfrac{1}{x}+\dfrac{1}{2x}\)) x 16 = 1 ⇒ \(\dfrac{24}{x}\) = 1 ⇒ \(x\)= 24
Vậy đội 1 làm riêng thì hoàn thành công việc trong số ngày là: 24 ngày
Đội 2 làm riêng thì hoàn thành công việc trong số ngày là: 1 : \(\dfrac{1}{2.24}\) = 48 (ngày)
Kết luận:..

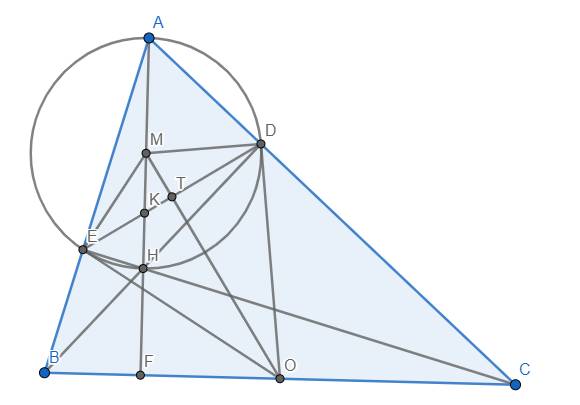
c) Dễ thấy M, O là tâm của đường tròn (ADHE) và (BEDC). Gọi bán kính của đường tròn (ADHE) là \(R\)
Gọi T là giao điểm của OM và DE.
Ta thấy vì \(OD=OE,MD=ME\) nên OM là trung trực của DE \(\Rightarrow OM\perp DE\) tại T
Xét tam giác MTK và MFO, có:
\(\widehat{FMO}\) chung, \(\widehat{MTK}=\widehat{MFO}=90^o\)
\(\Rightarrow\Delta MTK~\Delta MFO\left(g.g\right)\)
\(\Rightarrow\dfrac{MT}{MF}=\dfrac{MK}{MO}\)
\(\Rightarrow MT.MO=MF.MK\)
Tam giác MDO vuông tại D có đường cao DT nên \(MT.MO=MD^2\)
\(\Rightarrow MF.MK=MD^2\) \(=R^2\)
\(\Rightarrow MK=\dfrac{R^2}{MF}\) \(=\dfrac{R^2}{R+HF}\)
Do đó \(VP=2MK\left(AF+HF\right)\)
\(=\dfrac{2R^2}{R+HF}\left(2R+2HF\right)\) (thế \(AF=AH+HF=2R+HF\))
\(=4R^2\)
\(=AH^2=VT\)
Vậy ta có đpcm.


a) Nhận thấy \(\widehat{OBK}=\widehat{OAK}=90^o\) \(\Rightarrow\) Tứ giác OAKB nội tiếp đường tròn (OK).
Mặt khác \(\widehat{OHK}=90^o\) nên \(H\in\left(OK\right)\)
\(\Rightarrow\) 5 điểm A, B, O, K, H cùng thuộc đường tròn (OK).
b) Từ câu a) \(\Rightarrow\) Tứ giác OAHB nội tiếp
\(\Rightarrow\widehat{IHB}=\widehat{IAO}\)
Từ đó dễ dàng chứng minh \(\Delta IHB~\Delta IAO\left(g.g\right)\)
\(\Rightarrow\dfrac{IH}{IA}=\dfrac{IB}{IO}\) \(\Rightarrow IA.IB=IH.IO\) (đpcm)
c) Gọi T là giao điểm của OK và AB.
Tính chất của 2 tiếp tuyến cắt nhau \(\Rightarrow OK\perp AB\) tại T
Tam giác OAK vuông tại A có đường cao AT nên \(OT.OK=OA^2\) (hệ thức lượng trong tam giác vuông)
Xét tam giác OTI và OHK, ta có:
\(\widehat{HOK}\) chung , \(\widehat{OTI}=\widehat{OHK}=90^o\)
\(\Rightarrow\Delta OTI~\Delta OHK\left(g.g\right)\)
\(\Rightarrow\dfrac{OT}{OH}=\dfrac{OI}{OK}\)
\(\Rightarrow OT.OK=OH.OI\)
Mà \(OT.OK=OA^2\) (cmt) \(\Rightarrow OH.OI=OA^2\)
\(\Rightarrow OI=\dfrac{OA^2}{OH}\) là một hằng số
\(\Rightarrow\) I thuộc đường tròn \(\left(O;\dfrac{OA^2}{OH}\right)\) cố định
Hơn nữa I nằm trên đường thẳng OH cố định nên I cố định
\(\Rightarrow\) AB đi qua I cố định.