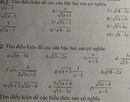
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=36+64=100\Rightarrow BC=10\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=x=\frac{AB^2}{BC}=\frac{36}{10}=\frac{18}{5}\)cm
* Áp dụng hệ thức : \(AC^2=CH.BC\Rightarrow CH=y=\frac{AC^2}{BC}=\frac{64}{10}=\frac{32}{5}\)cm
tổng 1+2+3+..+có bao nhiêu số hạng đểkeets quả của tổng bằng 190

\(\sqrt{4x^2-4x+1}=3x-2\)
\(\sqrt{\left(2x-1\right)^2}=3x-2\)
\(\left|2x-1\right|=3x-2\)
\(\orbr{\begin{cases}2x-1=3x-2\\2x-1=-3x+2\end{cases}}\)
\(\orbr{\begin{cases}1=x\\5x=1\end{cases}}\)
\(\orbr{\begin{cases}x=1\\x=\frac{1}{5}\end{cases}}\)
ĐKXĐ: \(x\ge\frac{2}{3}\)
Ta có : \(\sqrt{4x^2-2x+1}+2=3x\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=3x-2\)
\(\Leftrightarrow|2x-1|=3x-2\)
\(\Leftrightarrow2x-1=3x-2\)(do \(x\ge\frac{2}{3}\))
\(\Leftrightarrow x=1\left(TM\right)\)
Vậy tập nghiệm của PT là \(S=\left\{1\right\}\)

a) ĐK: \(x\ge\frac{1}{2}\).
\(\sqrt{2x-1}+\sqrt{x+4}=6\)
\(\Leftrightarrow\sqrt{2x-1}-3+\sqrt{x+4}-3=0\)
\(\Leftrightarrow\frac{2x-1-9}{\sqrt{2x-1}+3}+\frac{x+4-9}{\sqrt{x+4}+3}=0\)
\(\Leftrightarrow\left(x-5\right)\left(\frac{2}{\sqrt{2x-1}+3}+\frac{1}{\sqrt{x+4}+3}\right)=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\).
b) ĐK: \(x\ge\frac{1}{2}\).
\(\sqrt{x+3}-\sqrt{2x-1}=1\)
\(\Leftrightarrow\sqrt{x+3}-2+1-\sqrt{2x-1}=0\)
\(\Leftrightarrow\frac{x+3-4}{\sqrt{x+3}+2}+\frac{1-\left(2x-1\right)}{1+\sqrt{2x-1}}=0\)
\(\Leftrightarrow\left(x-1\right)\left(\frac{1}{\sqrt{x+3}+2}-\frac{2}{1+\sqrt{2x-1}}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\\frac{1}{\sqrt{x+3}+2}=\frac{2}{1+\sqrt{2x-1}}\left(1\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow2\sqrt{x+3}+4=1+\sqrt{2x-1}\)
Có \(4>1,2\sqrt{x+3}=\sqrt{4x+12}>\sqrt{2x-1}\)
do đó phương trình \(\left(1\right)\)vô nghiệm.
a) ĐK : x >= 1/2
\(\Leftrightarrow\left(\sqrt{2x-1}-3\right)+\left(\sqrt{x+4}-3\right)=0\)
\(\Leftrightarrow\frac{2x-1-9}{\sqrt{2x-1}+3}+\frac{x+4-9}{\sqrt{x+4}+3}=0\)
\(\Leftrightarrow\left(x-5\right)\left(\frac{2}{\sqrt{2x-1}+3}+\frac{1}{\sqrt{x+4}+3}\right)=0\)(1)
Dễ thấy với x >= 1/2 thì \(\frac{2}{\sqrt{2x-1}+3}+\frac{1}{\sqrt{x+4}+3}>0\)
nên (1) <=> x - 5 = 0 <=> x = 5 (tm)
Vậy phương trình có nghiệm x = 5

ĐK: \(x\ge1,y\ge2,z\ge3\).
\(x+y+z-2\sqrt{x-1}-4\sqrt{y-2}-6\sqrt{z-3}+8=0\)
\(\Leftrightarrow x-1-2\sqrt{x-1}+1+y-2-4\sqrt{y-2}+4+z-3-6\sqrt{z-3}+9=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2+\left(\sqrt{y-2}-2\right)^2+\left(\sqrt{z-3}-3\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x-1}-1=0\\\sqrt{y-2}-2=0\\\sqrt{z-3}-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\\z=12\end{cases}}\)(tm)

Harley chuyên Lam Sơn mới thi thì làm gì có chuyện trùng được bro(:

\(a,\sqrt{x-1}+\sqrt{9-x}=4\)
\(ĐKXĐ:1\le x\le9\)
\(\sqrt{x-1}=4-\sqrt{9-x}\)
\(x-1=16-8\sqrt{9-x}+9-x\)
\(26-8\sqrt{9-x}-2x=0\)
\(13-4\sqrt{9-x}-x=0\)
\(9-x-4\sqrt{9-x}+4=0\)
\(\left(\sqrt{9-x}-2\right)^2=0\)
\(\sqrt{9-x}=2\)
\(9-x=4\)
\(x=5\left(TM\right)\)
\(\sqrt{2x-1}+\sqrt{x+4}=6\)
\(ĐKXĐ:x\ge\frac{1}{2}\)
\(x+4=36-12\sqrt{2x-1}+2x-1\)
\(x+4=35-12\sqrt{2x-1}+2x\)
\(31-12\sqrt{2x-1}+x=0\)
\(\left(31+x\right)^2=\left(12\sqrt{2x-1}\right)^2\)
\(961+62x+x^2=144\left(2x-1\right)\)
\(961+62x+x^2=288x-144\)
\(x^2-226x+1105=0\)
\(\sqrt{\Delta}=216\)
\(x_1=\frac{226+216}{2}=221\left(TM\right)\)
\(x_2=\frac{226-216}{2}=5\left(TM\right)\)
................................................. tui ko bít

ĐKXĐ : \(y+\frac{1}{y}\ge0;y\ne0\)
Ta có : \(\hept{\begin{cases}x+\frac{1}{x^2+1}=y+\frac{1}{y^2+1}\left(1\right)\\x^2+2x.\sqrt{y+\frac{1}{y}}=8x-1\left(2\right)\end{cases}}\)
(1) \(\Leftrightarrow\left(x-y\right)-\frac{x^2-y^2}{\left(x^2+1\right)\left(y^2+1\right)}=0\) \(\Leftrightarrow\left(x-y\right)\left(1-\frac{x+y}{\left(x^2+1\right)\left(y^2+1\right)}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\1-\frac{x+y}{\left(x^2+1\right)\left(y^2+1\right)}=0\end{cases}}\)
Với x = y thay vào (2) ; ta có : \(x^2+2x\sqrt{x+\frac{1}{x}}=8x-1\)
\(\Leftrightarrow x+2\sqrt{x+\frac{1}{x}}=8-\frac{1}{x}\) ( vì x = y mà y khác 0 => x khác 0 )
Đặt \(a=\sqrt{x+\frac{1}{x}}\) rồi giải p/t
Với : \(1-\frac{x+y}{\left(x^2+1\right)\left(y^2+1\right)}=0\) \(\Leftrightarrow\frac{x^2y^2+y^2+x^2+1-x-y}{\left(x^2+1\right)\left(y^2+1\right)}=0\)
\(\Leftrightarrow\frac{\left(x-\frac{1}{2}\right)^2+\left(y-\frac{1}{2}\right)^2+\frac{1}{2}+x^2y^2}{\left(x^2+1\right)\left(y^2+1\right)}=0\)
Dễ thấy : VT > 0 => PTVN
....

o)\(\frac{2\sqrt{3x+4}}{\sqrt{15-3x}}\)có nghĩa \(\Leftrightarrow\hept{\begin{cases}3x+4\ge0\\15-3x>0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge-\frac{4}{3}\\x< 5\end{cases}}\)\(\Leftrightarrow-\frac{4}{3}\le x< 5\)
f)\(\sqrt{x}.\frac{x}{2\sqrt{3x-5}}\)có nghĩa \(\Leftrightarrow\hept{\begin{cases}x\ge0\\3x-5>0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge0\\x>\frac{5}{3}\end{cases}}\)
Sorry nha ,vừa nãy không đọc kĩ yêu cầu của bạn =))