Dùng Cách phối hợp nhiều phương pháp em nhé! 

Đó là phương pháp chặn kết hợp với tìm nghiệm nguyên.

     Gọi số đó là A thì theo bài ra ta có:

             A = 2023.k + 228 (k \(\in\) N* )

             A = 2024n + 218 (n \(\in\) N*)

   ⇒ 2023k + 228 = 2024n + 218

    ⇒ 2024n + 218 - 228 = 2023k

     ⇒ 2024n - 10 = 2023k

      ⇒ k = \(\dfrac{2024n-10}{2023}\)    

      ⇒ k = n + \(\dfrac{n-10}{2023}\)    

   vì k nguyên nên   n -  10 ⋮ 2023

                            ⇒n - 10 \(\in\) B(2023) = {0; 2023;...;}

                            ⇒ n \(\in\) {10; 2033;..;} (1)

     Vì A là số có 5 chữ số nên A ≤ 99999 

   ⇒ 2024n + 218 ≤ 99999

       2024n            ≤ 99999 - 218

      2024n             ≤ 99781

              n             ≤ 99781 : 2024

              n             ≤ 49,298 (2)

Kết hợp 1 và (2) ta có: n = 10

Vậy số cần tìm là: 2024 x 10 + 218 = 20458

Kết luận:...

=20458

Lời giải:

$12A=1.5.12+5.9.(13-1)+9.13(17-5)+13.17(21-9)+....+77.81(85-73)+81.85(89-77)$

$=60+(5.9.13+9.13.17+13.17.21+...+77.81.85+81.85.89)-(1.5.9+5.9.13+9.13.17+...+73.77.81+77.81.85)$

$=60+81.85.89 - 1.5.9=612780$

A = 1.5 + 5.9 + 9.13 + ... + 81.85

A = \(\dfrac{12}{12}\)(1.5 + 5.9 + 9.13 + 81.85)

A = \(\dfrac{1}{12}\).(1.5.12 + 5.9.12.+ 9.13.12 + ...+ 81.85.12]

A = \(\dfrac{1}{12}\).[1.5.(9 + 3) + 5.9.(13 - 1) + 9.13.(17 - 5) +...+ 81.85.(89 - 77)]

^{A = \(\dfrac{1}{12}\).[1.5.9 + 1.3.5 + 5.9.13 - 5.9.1 + 9.13.17 - 9.13.5 + ...+ 81.85.89 - 81.85.77]}

A = \(\dfrac{1}{12}\).[1.3.5 + 81.85.89]

A = \(\dfrac{1}{12}\).[15 + 612765]

A = \(\dfrac{1}{12}\).612780

A = 51065

 Ta có \(a^n-a^{n-4}=a^{n-4}\left(a^4-1\right)=N\)

 Ta thấy vì \(a^{n-4}\) và \(a^4-1\) không cùng tính chẵn lẻ nên \(N⋮2\)

 Mặt khác, ta thấy nếu \(a⋮3\) thì hiển nhiên \(N⋮3\). Nếu \(a⋮̸3\) thì \(a^2\) chia 3 dư 1 (tính chất số chính phương), dẫn tới \(a^4=\left(a^2\right)^2\) chỉ có thể chia 3 dư 1 hay \(a^4-1⋮3\) với mọi \(a⋮̸3\). Vậy \(N⋮3\)

 Ta cần chứng minh \(N⋮5\).

 Dễ thấy điều này đúng nếu \(a⋮5\) 

 Với \(a⋮̸5\), khi đó \(a^2\) chia 5 dư 1 hoặc 4 (tính chất của số chính phương), suy ra \(a^4=\left(a^2\right)^2\) chia 5 chỉ có thể dư 1 (cũng là tính chất của số chính phương). Dẫn đến \(a^4-1⋮5\) với mọi \(a⋮̸5\). Vậy \(N⋮5\).

 Do đó \(N⋮2.3.5=30\) (đpcm)

a; \(x\) + 6 ⋮ \(x\) + 1 (\(x\) ≠ - 1)

   \(x\) + 1 + 5 ⋮ \(x\) + 1

    \(x\) + 1 \(\in\) Ư(5) = {-5; -1; 1; 5}

    \(x\)       \(\in\) {-6; -2; 0; 4}

   \(x\) + 6 ⋮ \(x\) + (-1)     (\(x\) ≠ 1)

   \(x\) + - 1 + 7  ⋮ \(x\) - 1

                  7 ⋮ \(x\) - 1

 \(x\) - 1  \(\in\) Ư(7) = {-7; -1; 1; 7}

 \(x\)        \(\in\) {-6; 0; 2; 8}

b;   \(x\) + 6 ⋮ \(x\) - 2 (đk \(x\) ≠ 2)

 \(x\) - 2 + 8 ⋮ \(x\) - 2

            8 ⋮  \(x\) - 2

\(x\) - 2 \(\in\) Ư(8) = {-8; -4; -2; -1; 1; 2; 4; 8}

\(x\) \(\in\) {-6; -2; 0; 1; 3; 4; 10}

\(x\) + 6 ⋮ \(x\) + (-2)

\(x\) + 6  ⋮ \(x\) - 2

giống với ý trên

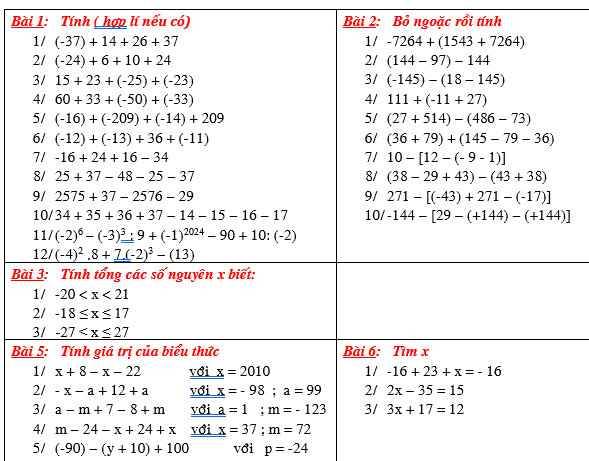
Bài 1:

1. $=[(-37)+37]+(14+26)=0+40=40$

2. $=[(-24)+24]+6+10=0+6+10=16$

3. $=[15+(-25)]+[23+(-23)]=-10+0=-10$

4. $=[60+(-50)]+[33+(-33)]=10+0=10$

5. $=-(16+14)+[(-209)+209]=-30+0=-30$

Bài 1:

6. $=-(11+12+13)+36=-36+36=0$

7. $=[(-16)+16]-(34-24)=0-10=-10$

8. $=(25-25)+(37-37)-48=0+0-48=-48$

9. $=(2575-2576)+(37-29)=-1+8=7$

10. $=(34-14)+(35-15)+(36-16)+(37-17)=20+20+20+20=20.4=80$

11. $=64-(-3)+1-90+(-5)=64+3+1-90-5=68-90-5=-27$

12. $=16.8-7.8-13=8(16-7)-13=8.9-13=72-13=59$

Sai đề hay sao ý bạn nhỉ?

mình cũng không biết nữa thầy giáo mình cho vậy á

\(5x-y\left(x-3\right)=8\)

\(\Leftrightarrow5x-15-y\left(x-3\right)=8-15\)

\(\Leftrightarrow5\left(x-3\right)-y\left(x-3\right)=-7\)

\(\Leftrightarrow\left(5-y\right)\left(x-3\right)=-7\)

Bảng giá trị:

Vậy các cặp số nguyên thỏa mãn là:

\(\left(x;y\right)=\left(4;12\right);\left(10;6\right);\left(-4;4\right);\left(2;-2\right)\)

1 lon hon

1

Pịa !!!

Gọi số ngày cả ba tàu cập cảng vào lần tiếp theo là \(x\)(điều kiện: ngày, \(x\inℕ^∗\)), theo đề bài, ta có:

\(x⋮6\\ x⋮12\\ x⋮30\)

\(x\) nhỏ nhất

\(\Rightarrow x\in BC\left(6,12,30\right)\)

⇒ Ta có:

\(6=2.3\\ 12=2^2.3\\ 30=2.3.5\)

\(\Rightarrow BCNN\left(6,12,30\right)=2^2.3.5=60\)

\(\Rightarrow BC\left(6,12,15\right)=B\left(60\right)=\left\{0;60;120;180;..\right\}\)

Mà x nhỏ nhất khác 0 ⇒ x = 60.

⇒ Sau ít nhất 60 ngày thì cả 3 tàu lại cùng nhau cập cảng.

Huhuhuhuhuh