
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
1: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(A=\left(\dfrac{x+3}{2x+2}+\dfrac{3}{1-x^2}-\dfrac{x+1}{2x-2}\right):\dfrac{3}{2x^2-2}\)
\(=\left(\dfrac{x+3}{2\left(x+1\right)}-\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+1}{2\left(x-1\right)}\right)\cdot\dfrac{2\left(x-1\right)\left(x+1\right)}{3}\)
\(=\dfrac{\left(x+3\right)\left(x-1\right)-6-\left(x+1\right)^2}{2\left(x+1\right)\left(x-1\right)}\cdot\dfrac{2\left(x-1\right)\left(x+1\right)}{3}\)
\(=\dfrac{x^2+2x-3-6-x^2-2x-1}{3}=\dfrac{-10}{3}\) không phụ thuộc vào biến x
Bài 4:
1:
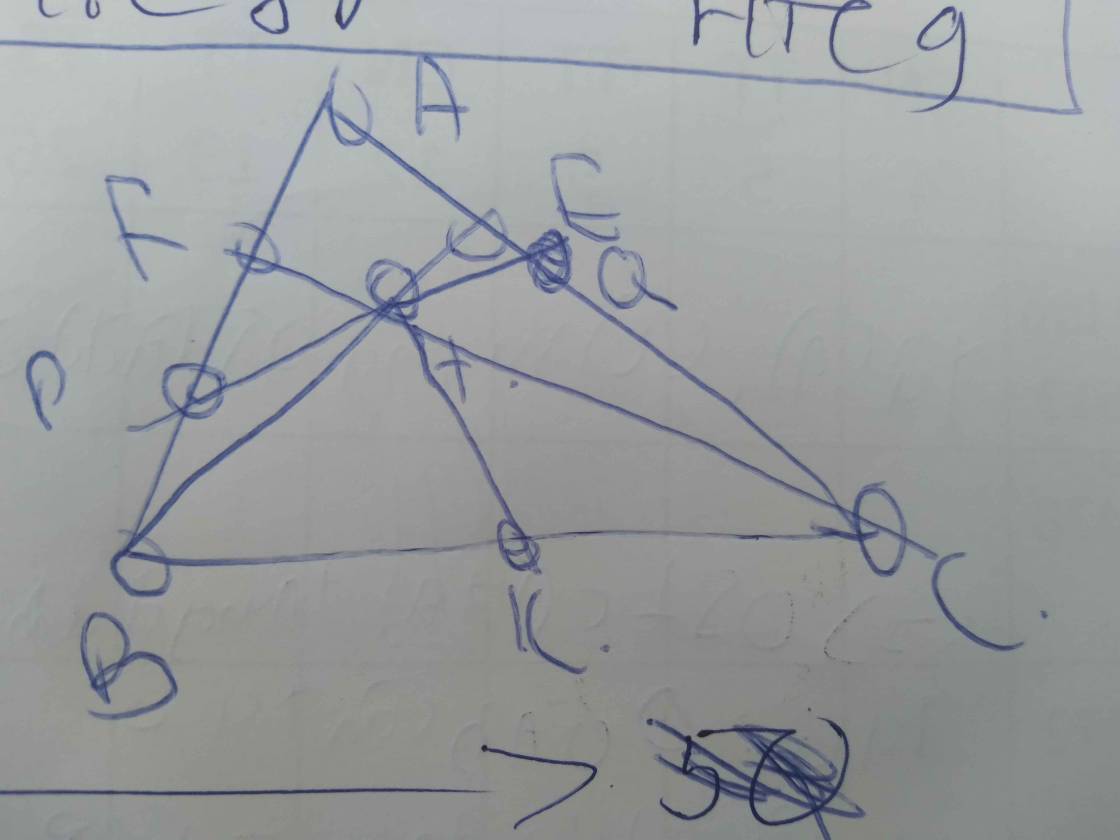
Xét ΔCAF vuông tại A và ΔCHE vuông tại H có
\(\widehat{ACF}=\widehat{HCE}\)
Do đó: ΔCAF~ΔCHE
2: Ta có ΔCAF~ΔCHE
=>\(\widehat{CFA}=\widehat{CEH}\)
mà \(\widehat{CEH}=\widehat{AEF}\)(hai góc đối đỉnh)
nên \(\widehat{AEF}=\widehat{AFE}\)
=>ΔAEF cân tại A
Xét ΔCAH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ACH}\) chung
Do đó: ΔCAH~ΔCBA
=>\(\dfrac{CA}{CB}=\dfrac{CH}{CA}\left(1\right)\)
Xét ΔCAH có CE là phân giác
nên \(\dfrac{HE}{AE}=\dfrac{CH}{CA}\left(2\right)\)
Xét ΔCAB có CF là phân giác
nên \(\dfrac{AF}{FB}=\dfrac{CA}{CB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{HE}{AE}=\dfrac{AF}{FB}\)
=>\(HE\cdot FB=AE\cdot AF=AE^2\)

Gọi A là biến cố "Lấy được viên bi màu đỏ"
Trong túi có 8 viên màu đỏ nên n(A)=8
=>\(P\left(A\right)=\dfrac{8}{19}\)

1:
a: 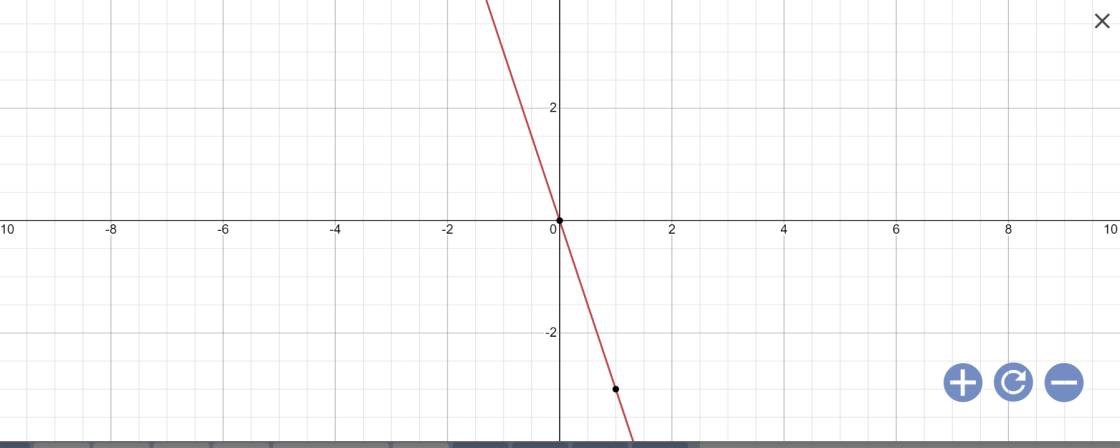
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=x+b
Thay x=-1 và y=3 vào (d3), ta được:
b-1=3
=>b=4
Vậy: (d3): y=x+4
Bài 2:
Gọi số sản phẩm tổ 1 phải sản xuất theo kế hoạch là x(sản phẩm)
(ĐIều kiện: \(x\in Z^+\))
Số sản phẩm tổ 2 phải sản xuất theo kế hoạch là:
900-x(sản phẩm)
Số sản phẩm thực tế tổ 1 làm được là:
\(x\left(1+20\%\right)=1,2x\left(sảnphẩm\right)\)
Số sản phẩm thực tế tổ 2 làm được là:
\(\left(900-x\right)\left(1+15\%\right)=1,15\left(900-x\right)\left(sảnphẩm\right)\)
Tổng số sản phẩm là 1055 sản phẩm nên ta có:
1,2x+1,15(900-x)=1055
=>0,05x+1035=1055
=>0,05x=20
=>x=400(nhận)
Vậy: số sản phẩm tổ 1 phải sản xuất theo kế hoạch là 400 sản phẩm
số sản phẩm tổ 2 phải sản xuất theo kế hoạch là 900-400=500 sản phẩm

a) \(2x=7+x\)
\(\Leftrightarrow2x-x=7\)
\(\Leftrightarrow x=7\)
Vậy \(S=\{7\}\)
b) \(\dfrac{x-3}{5}+\dfrac{1+2x}{3}=6\)
\(\Leftrightarrow\dfrac{3\left(x-3\right)}{15}+\dfrac{5\left(1+2x\right)}{15}=6\)
\(\Leftrightarrow\dfrac{3x-9+5+10x}{15}=6\)
\(\Leftrightarrow13x-4=90\)
\(\Leftrightarrow13x=94\)
\(\Leftrightarrow x=\dfrac{94}{13}\)
Vậy \(S=\left\{\dfrac{94}{13}\right\}\).

Câu 2: \(\dfrac{x}{6}+\dfrac{y}{8}=1\)
=>\(\dfrac{4x+3y}{24}=1\)
=>4x+3y=24
=>4x+3y-24=0
Khoảng cách từ O đến đường thẳng 4x+3y-24=0 là:
\(d\left(O;4x+3y-24=0\right)=\dfrac{\left|0\cdot4+0\cdot3-24\right|}{\sqrt{3^2+4^2}}=\dfrac{24}{5}=4,8\)

a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
\(\widehat{BED}\) chung
do đó: ΔBDE~ΔDCE
b:
Ta có: CH\(\perp\)DE
DB\(\perp\)DE
Do đó: CH//DB
Xét ΔHCD vuông tại H và ΔCDB vuông tại C có
\(\widehat{HCD}=\widehat{CDB}\)(HC//DB)
Do đó: ΔHCD~ΔCDB
=>\(\dfrac{HC}{CD}=\dfrac{CD}{DB}\)
=>\(CD^2=HC\cdot DB\)
c: Ta có: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
=>OB=OD(1)
Xét ΔEOD có HK//OD
nên \(\dfrac{HK}{OD}=\dfrac{EK}{EO}\left(2\right)\)
Xét ΔEOB có KC//OB
nên \(\dfrac{KC}{OB}=\dfrac{EH}{EO}\left(3\right)\)
Từ (1),(2),(3) suy ra KH=KC
=>K là trung điểm của HC

a: Chu vi đáy là 2x3=6(m)
Diện tích xung quanh là \(6\cdot3=18\left(m^2\right)\)
b: Diện tích cần sơn là \(18\cdot3=54\left(m^2\right)\)
Số tiền phải trả là \(54\cdot30000=1620000\left(đồng\right)\)

a) Xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là:
\(8:20=\dfrac{8}{20}=\dfrac{2}{5}\)
Vậy xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là \(\dfrac{2}{5}\).
b) Số lần xuất hiện mặt N là:
\(15-9=6\) ( lần )
Xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là:
\(6:15=\dfrac{6}{15}=\dfrac{2}{5}\)
Vậy xác suất thực nghiệm của biến cố mặt xuất hiện của đồng xu là mặt N là \(\dfrac{2}{5}\).
a) Xác suất thực nghiệm của biến cố xuất hiện mặt N:
P = 8/20 = 2/5
b) Xác suất thực nghiệm của biến cố xuất hiện mặt S:
P = 9/15 = 3/5






a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}=\dfrac{AB}{HB}\)
=>\(AB\cdot HA=AC\cdot HB\)
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\dfrac{BC}{BA}=\dfrac{AC}{HA}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=\dfrac{300}{25}=12\left(cm\right)\)
=>\(HB=\sqrt{15^2-12^2}=9\left(cm\right)\)
c:
Xét ΔBAH có BI là phân giác
nên \(\dfrac{IA}{IH}=\dfrac{BA}{BH}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DC}{DA}=\dfrac{BC}{BA}\left(2\right)\)
Ta có: ΔBHA~ΔBAC
=>\(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
=>\(\dfrac{BC}{BA}=\dfrac{BA}{BH}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IA}{IH}=\dfrac{DC}{DA}\)
=>\(IA\cdot DA=DC\cdot IH\)