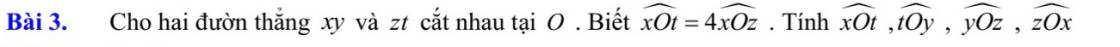Lời giải:

$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=12$

$\Rightarrow \frac{a^2+b^2+c^2}{abc}=12$

$\Rightarrow a^2+b^2+c^2=12abc$

$\Rightarrow (a+b+c)^2-2(ab+bc+ac)=12abc$

$\Rightarrow -2(ab+bc+ac)=12abc$

$\Rightarrow \frac{ab+bc+ac}{abc}=\frac{12}{-2}$

$\Rightarrow M=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=-6$

Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

b: Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)

\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ABD}=\widehat{ACE}\)

Xét ΔABD và ΔACE có

AB=AC

\(\widehat{ABD}=\widehat{ACE}\)

BD=CE

Do đó: ΔABD=ΔACE

Ai làm câu d giúp mình với

Lời giải:

Theo tính chất tổng 3 góc trong 1 tam giác thì:

$\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}$

$=180^0-\frac{\widehat{B}}{2}-\frac{\widehat{C}}{2}$
$=\frac{360^0-(\widehat{B}+\widehat{C})}{2}$

$=\frac{360^0-(180^0-\widehat{A})}{2}=\frac{180^0+\widehat{A}}{2}$
Nếu $\widehat{BIC}=135^0$ thì:

$135^0=\frac{180^0+\widehat{A}}{2}$
$\Rightarrow 180^0+\widehat{A}=135^0.2=270^0$

$\Rightarrow \widehat{A}=270^0-180^0=90^0$

$\Rightarrow \triangle ABC$ vuông tại $A$

Hình vẽ:

Lời giải:
a.

$\frac{-9}{20}=-2,1.\frac{3}{14}$

b.

$\frac{-9}{20}=-2\frac{3}{4}:\frac{55}{9}$

Câu nào thế em nhỉ?

Số nguyên với số hữu tỉ không phải là một em nhé.

Số nguyên thuộc số hữu tỉ, nhưng số hữu tỉ chưa chắc đã là số nguyên.

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Xét ΔABO vuông tại B và ΔACO vuông tại C có

AO chung

AB=AC

Do đó: ΔABO=ΔACO

=>OB=OC

=>O nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Ta có: MB=MC

=>M nằm trên đường trung trực của BC(3)

Từ (1),(2),(3) suy ra A,M,O thẳng hàng

\(\widehat{xOt}=4\cdot\widehat{xOz}\)

mà \(\widehat{xOt}+\widehat{xOz}=180^0\)(hai góc kề bù)

nên \(\widehat{xOt}=180^0\cdot\dfrac{4}{5}=144^0;\widehat{xOz}=180^0-144^0=36^0\)

Ta có: \(\widehat{xOt}=\widehat{yOz}\)(hai góc đối đỉnh)

mà \(\widehat{xOt}=144^0\)

nên \(\widehat{yOz}=144^0\)

Ta có: \(\widehat{xOz}=\widehat{yOt}\)(hai góc đối đỉnh)

mà \(\widehat{xOz}=36^0\)

nên \(\widehat{yOt}=36^0\)

a: Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)

\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{ABD}=\widehat{ACE}\)

Xét ΔABD và ΔACE có

AB=AC

\(\widehat{ABD}=\widehat{ACE}\)

BD=CE

Do đó: ΔABD=ΔACE

=>AD=AE; \(\widehat{BAD}=\widehat{CAE};\widehat{ADB}=\widehat{AEC}\)

Xét ΔHBD vuông tại H và ΔKCE vuông tại K có

BD=CE

\(\widehat{HDB}=\widehat{KEC}\)

Do đó: ΔHBD=ΔKCE

=>HB=CK

b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có

AB=AC

BH=CK

Do đó: ΔAHB=ΔAKC

c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)(hai góc đối đỉnh)

\(\widehat{OCB}=\widehat{KCE}\)(hai góc đối đỉnh)

mà \(\widehat{HBD}=\widehat{KCE}\)(ΔHBD=ΔKCE)

nên \(\widehat{OBC}=\widehat{OCB}\)

=>ΔOBC cân tại O

d: Xét ΔABO và ΔACO có

AB=AC

BO=CO

AO chung

Do đó: ΔABO=ΔACO

=>\(\widehat{BAO}=\widehat{CAO}\)

Ta có: \(\widehat{DAB}+\widehat{BAO}=\widehat{DAO}\)

\(\widehat{EAC}+\widehat{CAO}=\widehat{EAO}\)

mà \(\widehat{DAB}=\widehat{EAC};\widehat{BAO}=\widehat{CAO}\)

nên \(\widehat{DAO}=\widehat{EAO}\)

=>AO là phân giác của góc DAE

e: IB=IC

=>I nằm trên đường trung trực của BC(1)

Ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(3)

Từ (1),(2),(3) suy ra A,O,I thẳng hàng