giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


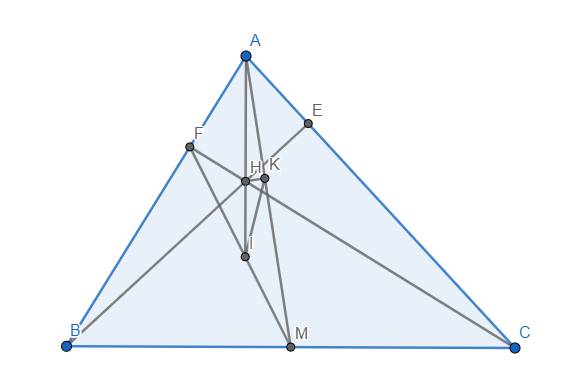
Nếu bạn nhìn trong hình này thì nó có phải là phân giác đâu?

\(A=\sqrt{\left(3+2\sqrt{2}\right)^2}-\sqrt{8}\)
\(A=\left|3+2\sqrt{2}\right|-\sqrt{2^2\cdot2}\)
\(A=\left(3+2\sqrt{2}\right)-2\sqrt{2}\)
\(A=3+2\sqrt{2}-2\sqrt{2}\)
\(A=3\)

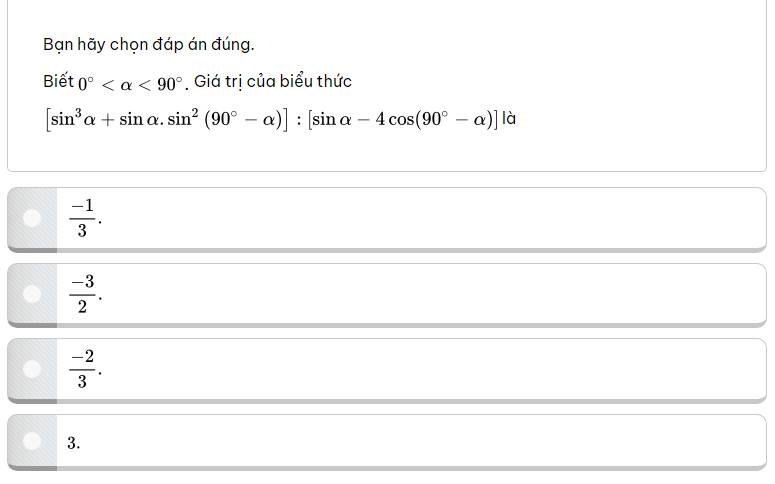
\(\left[sin^3a+sina\cdot sin^2\left(90-a\right)\right]:\left[sina-4\cdot cos\left(90-a\right)\right]\)
\(=\left[sin^3a+sina\cdot cos^2a\right]:\left[sina-4\cdot sina\right]\)
\(=\dfrac{sina\left(sin^2a+cos^2a\right)}{-3\cdot sina}=\dfrac{1}{-3}=-\dfrac{1}{3}\)

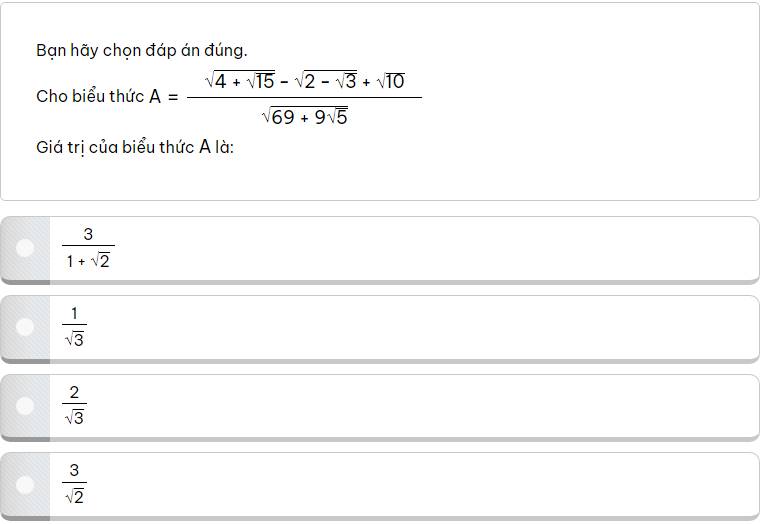
\(A=\dfrac{\sqrt{4+\sqrt{15}}-\sqrt{2-\sqrt{3}}+\sqrt{10}}{\sqrt{69+9\sqrt{5}}}\)
\(=\dfrac{\sqrt{8+2\sqrt{15}}-\sqrt{4-2\sqrt{3}}+2\sqrt{5}}{\sqrt{138+18\sqrt{5}}}\)
\(=\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{3}+1+2\sqrt{5}}{\sqrt{135+2\cdot3\sqrt{15}\cdot\sqrt{3}+3}}\)
\(=\dfrac{3\sqrt{5}+1}{\sqrt{\left(3\sqrt{15}+\sqrt{3}\right)^2}}=\dfrac{3\sqrt{5}+1}{3\sqrt{15}+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{3}}\)

pt đã cho \(\Leftrightarrow x^2-\left(y+1\right)x-2y^2+5y-6=0\) (*)
Ta tính được \(\Delta=9y^2-18y+25>0\) với mọi y.
Để (*) có nghiệm nguyên thì \(9y^2-18y+25\) là số chính phương
\(\Leftrightarrow9y^2-18y+25=z^2\left(z\inℕ,z\ge4\right)\)
\(\Leftrightarrow\left(3y-3\right)^2+16=z^2\)
\(\Leftrightarrow\left(z+3y-3\right)\left(z-3y+3\right)=16\)
Ta có bảng sau:
| \(z+3y-3\) | 1 | -1 | 16 | -16 | 2 | 8 | -2 | -8 | 4 | -4 |
| \(z-3y+3\) | 16 | -16 | 1 | -1 | -8 | -2 | 8 | 2 | 4 | -4 |
| \(z\) | \(\dfrac{17}{2}\)(l) | -8 | 8 | \(-\dfrac{11}{2}\)(l) | -3 | 3 | 3 | -3 | 4 | -4 |
| \(y\) | \(\dfrac{10}{3}\)(l) | \(\dfrac{10}{3}\)(l) | \(\dfrac{8}{3}\)(l) | \(\dfrac{8}{3}\)(l) | \(-\dfrac{2}{3}\) | \(-\dfrac{2}{3}\)(l) | 1 | 1 | ||
Vậy \(y=1\) \(\Rightarrow x^2-2x-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Vậy pt đã cho có các nghiệm nguyên là \(\left(-1;1\right)\) và \(\left(3;1\right)\)

Gọi lãi suất mỗi năm của ngân hàng là x(%/năm)
(ĐK: x>0)
Sau 1 năm tổng số tiền (cả gốc lẫn lãi) có được là:
\(150000000\left(1+x\right)\left(đồng\right)\)
Sau 2 năm tổng số tiền (cả gốc lẫn lãi) có được là:
\(150000000\left(1+x\right)\left(1+x\right)=150000000\left(1+x\right)^2\left(đồng\right)\)
Theo đề, ta có:
\(150000000\left(x+1\right)^2=168540000\)
=>\(\left(x+1\right)^2=\dfrac{2809}{2500}\)
=>\(x+1=\dfrac{53}{50}\)
=>\(x=\dfrac{3}{50}=0,06\)(nhận)
=>Lãi suất của ngân hàng đó là 6%/năm

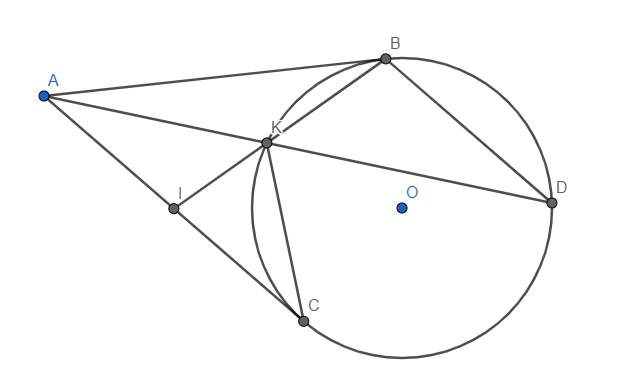
b) Do BD//AC nên \(\widehat{KAI}=\widehat{KDB}\) (2 góc so le trong)
Lại có \(\widehat{ABI}=\widehat{ABK}=\widehat{BDK}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BK.
\(\Rightarrow\widehat{KAI}=\widehat{KBA}\)
c) I là trung điểm AC chứ không phải BC nhé.
Xét tam giác IAK và IBA, ta có:
\(\widehat{AIB}\) chung, \(\widehat{IAK}=\widehat{IBA}\left(cmt\right)\)
\(\Rightarrow\Delta IAK\sim\Delta IBA\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IK}{IA}\)
\(\Rightarrow IA^2=IB.IK\)
\(\Rightarrow IA=IC\) (vì theo câu a, \(IC^2=IB.IK\))
\(\Rightarrow\) I là trung điểm AC.
d) CK vuông góc với đường nào trong đề bài chưa nói nhé.

a: Xét tứ giác MIKC có \(\widehat{MIC}=\widehat{MKC}=90^0\)
nên MIKC là tứ giác nội tiếp
Xét tứ giác MIAH có \(\widehat{MIA}+\widehat{MHA}=90^0+90^0=180^0\)
nên MIAH là tứ giác nội tiếp
Xét tứ giác MKBH có \(\widehat{MKB}+\widehat{MHB}=90^0+90^0=180^0\)
nên MKBH là tứ giác nội tiếp
b: Ta có: MIKC là tứ giác nội tiếp
=>\(\widehat{MIK}+\widehat{MCK}=180^0\)
=>\(\widehat{MIK}=180^0-\widehat{MCB}\)
Ta có: HAIM là tứ giác nội tiếp
=>\(\widehat{MIH}=\widehat{MAH}\)
mà \(\widehat{MAH}=\widehat{MCB}\left(=180^0-\widehat{MAB}\right)\)
nên \(\widehat{MIH}=\widehat{MCB}\)
=>\(\widehat{MIH}+\widehat{MIK}=180^0\)
=>K,I,H thẳng hàng

a: Xét tứ giác BEFC có \(\widehat{BEC}=\widehat{BFC}=90^0\)
nên BEFC là tứ giác nội tiếp
b: XétΔAFB vuông tại F và ΔAEC vuông tại E có
\(\widehat{FAB}\) chung
Do đó: ΔAFB~ΔAEC
=>\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\)
=>\(AF\cdot AC=AB\cdot AE\)