Tìm số nguyên a sao cho
2/3 bé hơn a-1/6 bé hơn 8/9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi x=-99 và y=99 thì \(x^4-y^4=\left(-99\right)^4-99^4=99^4-99^4=0\)


Số tiền phải trả khi mua 1 chiếc máy tính là:
\(700000\cdot\left(100\%-10\%\right)=630000\) (đồng)
Số tiền phải trả khi mua 7 cái bút là:
\(7\cdot10000\cdot\left(100\%-5\%\right)=66500\) (đồng)
Số tiền phải trả khi mua x quyển vở là:
\(x\cdot20000\cdot\left(100\%-20\%\right)=x\cdot20000\cdot80\%=16000x\) (đồng)
Biểu thức đại số thể hiện tổng số tiền phải trả là:
\(630000+66500+16000x=696500+16000x\)
máy tính sau khi giảm giá là:
700000 x (1 - 10%) = 630000 (đồng)
quyển vở sau khi giảm giá là:
20000 x (1 - 20%) = 16000 (đòng)
chiếc bút sau khi giảm giá là:
10000 x (1 - 5%) = 9,500 (đồng)
số tiền mua 1 chiếc máy tính là: 630000 đồng
số tiền mua 7 chiếc bút là: 7 x 9500 = 66500 đồng
số tiền mua x quyển vở là: 16000x đồng
BIỂU THỨC ĐẠI SỐ TỔNG SỐ TIỀN LÀ:
630000 + 66500 + 1600x

`#3107.101107`
`a)`
- Tổng của 2 số hữu tỉ khác dấu: \(-\dfrac{4}{15}=-\dfrac{13}{15}+\dfrac{9}{15}\)
`b)`
- Tích cảu 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{8}{15}\cdot\dfrac{1}{2}\)
`c)`
Thương của 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{16}{15}\div2\)

a; \(\dfrac{98}{99}\) > \(\dfrac{98}{100}\) (hai phân số dương có cùng tử số, phân số nào có mẫu lớn hơn thì phân số đó lớn hơn)
\(\dfrac{98}{100}\) > \(\dfrac{97}{100}\)(hai phân số dương có cùng mẫu số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn)
Vậy \(\dfrac{97}{100}\) < \(\dfrac{98}{99}\)
b; \(\dfrac{19}{18}\) = 1 + \(\dfrac{1}{18}\)
\(\dfrac{2021}{2020}\) = 1 + \(\dfrac{1}{2020}\)
\(\dfrac{1}{18}\) > \(\dfrac{1}{2020}\) (hai phân số dương có cùng tử số phân số nào có mẫu số nhỏ hơn thì phân số đó lớn hơn)
\(\dfrac{19}{18}\) > \(\dfrac{2021}{2020}\) (hai phân số phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn)
Vậy: \(\dfrac{19}{18}\) > \(\dfrac{2021}{2020}\)

a) \(\dfrac{2x+1}{9}=\dfrac{5}{x+1}\left(x\ne-1\right)\)
\(\Rightarrow\left(2x+1\right)\left(x+1\right)=9\cdot5=45\)
\(\Rightarrow2x^2+2x+x+1=45\)
\(\Rightarrow2x^2+3x-44=0\)
\(\Rightarrow2x^2+11x-8x-44=0\)
\(\Rightarrow x\left(2x+11\right)-4\left(2x+11\right)=0\)
\(\Rightarrow\left(x-4\right)\left(2x+11\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\2x=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{11}{2}\end{matrix}\right.\)
b) \(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\left(x\ne-\dfrac{1}{2}\right)\)
\(\Rightarrow\left(2x-1\right)\left(2x+1\right)=21\cdot3=63\)
\(\Rightarrow4x^2-1=63\)
\(\Rightarrow4x^2=64\)
\(\Rightarrow\left(2x\right)^2=8^2\)
\(\Rightarrow\left[{}\begin{matrix}2x=8\\2x=-8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
c) \(\dfrac{2x-1}{2}=\dfrac{5}{x}\left(x\ne0\right)\)
\(\Rightarrow x\left(2x-1\right)=5\cdot2=10\)
\(\Rightarrow2x^2-x=10\)
\(\Rightarrow2x^2-x-10=0\)
\(\Rightarrow2x^2+4x-5x-10=0\)
\(\Rightarrow2x\left(x+2\right)-5\left(x+2\right)=0\)
\(\Rightarrow\left(2x-5\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)
d) \(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\)
\(\Rightarrow15\cdot\dfrac{x-3}{3}=15\cdot\dfrac{2x+1}{5}\)
\(\Rightarrow5\left(x-3\right)=3\left(2x+1\right)\)
\(\Rightarrow5x-15=6x+3\)
\(\Rightarrow6x-5x=-18\)
\(\Rightarrow x=-18\)

Sửa đề:
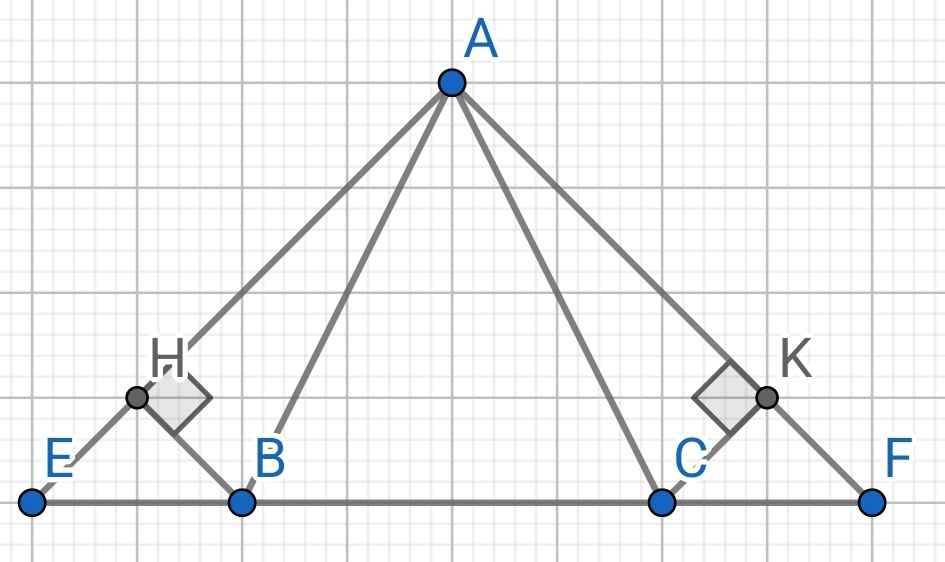
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF
a) Chứng minh tam giác AEF cân
b) vẽ BH vuông góc AE, CK vuông góc AF. CM tam giác EBH bằng tam giác FCK.
Giải
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB
Ta có:
∠ABC + ∠ABE = 180⁰ (kề bù)
∠ACB + ∠ACF = 180⁰ (kề bù)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABE = ∠ACF
Xét ∆ABE và ∆ACF có:
AB = AC (cmt)
∠ABE = ∠ACF (cmt)
BE = CF (gt)
⇒ ∆ABE = ∆ACF (c-g-c)
⇒ AE = AF (hai cạnh tương ứng)
⇒ ∆AEF cân tại A
b) Do ∆AEF cân tại A (cmt)
⇒ ∠AEF = ∠AFE
⇒ ∠HEB = ∠KFC
Xét hai tam giác vuông: ∆EBH và ∆FCK có:
BE = CF (gt)
∠HEB = ∠KFC (cmt)
⇒ ∆EBH = ∆FCK (cạnh huyền - góc nhọn)

\(0,75+\dfrac{3}{6}-\dfrac{8}{2}=\dfrac{5}{3}+x.\dfrac{-5}{6}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{3}{4}+\dfrac{3}{6}-\dfrac{8}{2}-\dfrac{5}{3}\\ \Rightarrow-\dfrac{5}{6}x=\dfrac{9}{12}+\dfrac{6}{12}-\dfrac{48}{12}-\dfrac{20}{12}\\ \Rightarrow-\dfrac{5}{6}x=-\dfrac{53}{12}\\ \Rightarrow x=\left(-\dfrac{53}{12}\right):\left(-\dfrac{5}{6}\right)\\ \Rightarrow x=\dfrac{53}{10}\)
Ta có:$\frac23< a-\frac16<\frac89$
$\Rightarrow \frac23+\frac16< a-\frac16+\frac16<\frac89+\frac16$
$\Rightarrow \frac56< a<\frac{19}{18}$
Mà a nguyên nên $a=1$
CẢM ƠN NHIỀU NHA