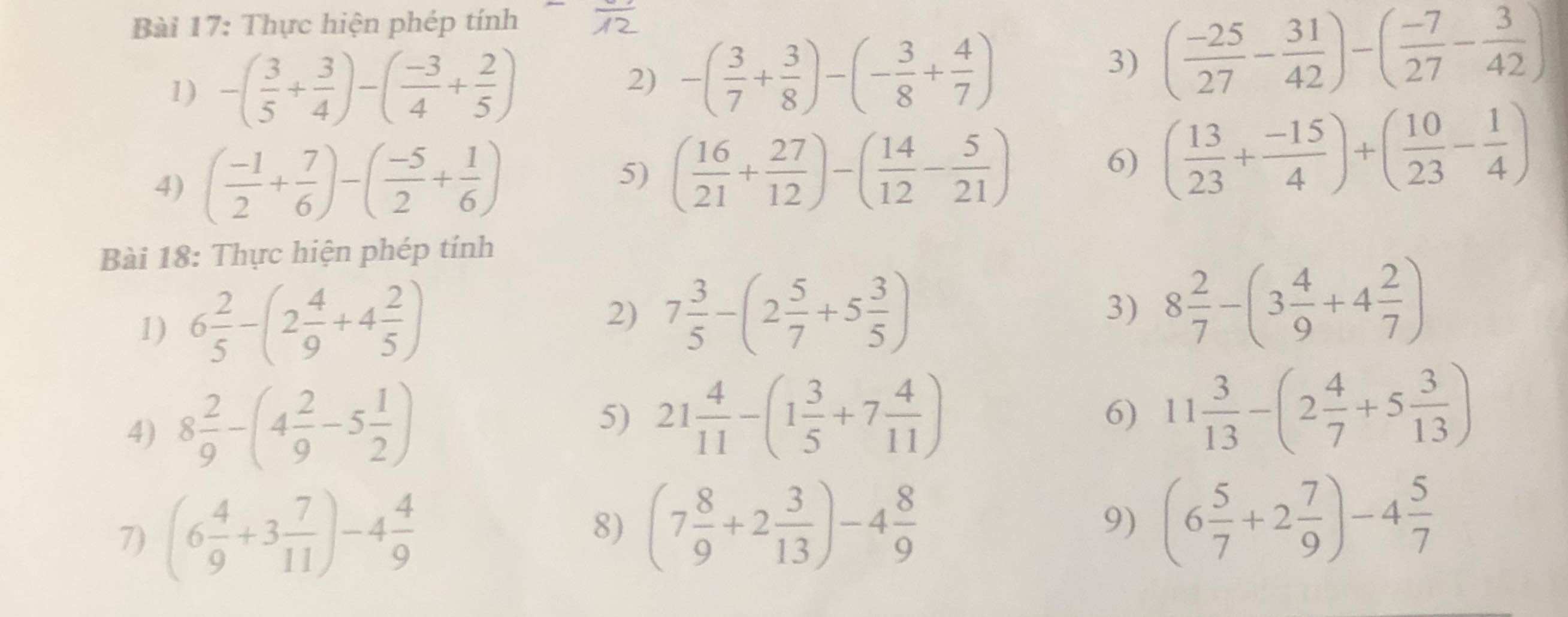Để \(\dfrac{12n+1}{30n-1}\) tối giản thì \(UCLN\left(12n+1,30n-1\right)=1\)

Đặt \(d=UCLN\left(12n+1,30n-1\right)\)

\(S=5\left(12n+1\right)-2\left(30n-1\right)=3\)

vì 12n+1 chia hết cho d và 30n-1 chia hết cho d

nên S chia hết cho d

suy ra 3 chia hết cho d. 

Do đó \(d\in\left\{1,3\right\}\)

Tuy nhiên, 12n+1 và 30n-1 không chia hết cho 3

nên d=1

Vậy, phân số \(\dfrac{12n+1}{30n-1}\) tối giản \(\forall n\inℕ\)

Gọi số ban đầu có dạng: \(\overline{abc}\)

a) Sau khi thêm chữ số 5 vào ban trái thì ta có số: \(\overline{5abc}\)

\(\overline{5abc}=5000+\overline{abc}\)

=> Số đó tăng thêm 5000 đơn vị 

b) Sau khi thêm chữ số 3 vào trên trái thì ta có: \(\overline{3abc}\)

\(\overline{3abc}=3000+\overline{abc}\)

=> Số đó tăng thêm 3000 đơn vị 

\(1)-\left(\dfrac{3}{5}+\dfrac{3}{4}\right)-\left(\dfrac{-3}{4}+\dfrac{2}{5}\right)\\ =-\dfrac{3}{5}-\dfrac{3}{4}+\dfrac{3}{4}-\dfrac{2}{5}\\ =\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\left(-\dfrac{3}{5}-\dfrac{2}{5}\right)\\ =-1\\ 2)-\left(\dfrac{3}{7}+\dfrac{3}{8}\right)-\left(-\dfrac{3}{8}+\dfrac{4}{7}\right)\\ =-\dfrac{3}{7}-\dfrac{3}{8}+\dfrac{3}{8}-\dfrac{4}{7}\\ =\left(\dfrac{3}{8}-\dfrac{3}{8}\right)+\left(-\dfrac{3}{7}-\dfrac{4}{7}\right)\\ =-1\\ 3)\left(\dfrac{-25}{27}-\dfrac{31}{42}\right)-\left(\dfrac{-7}{27}-\dfrac{3}{42}\right)\\ =-\dfrac{25}{27}-\dfrac{31}{42}+\dfrac{7}{27}+\dfrac{3}{42}\\ =\left(\dfrac{-25}{27}+\dfrac{7}{27}\right)+\left(\dfrac{-31}{42}+\dfrac{3}{42}\right)\\ =\dfrac{-18}{27}+\dfrac{-28}{42}\\ =\dfrac{-2}{3}+\dfrac{-2}{3}\\ =-\dfrac{4}{3}\)

Bài 17:

4: \(\left(-\dfrac{1}{2}+\dfrac{7}{6}\right)-\left(-\dfrac{5}{2}+\dfrac{1}{6}\right)\)

\(=-\dfrac{1}{2}+\dfrac{7}{6}+\dfrac{5}{2}-\dfrac{1}{6}\)

=2-1=1

5: \(\left(\dfrac{16}{21}+\dfrac{27}{12}\right)-\left(\dfrac{14}{12}-\dfrac{5}{21}\right)\)

\(=\dfrac{16}{21}+\dfrac{27}{12}-\dfrac{14}{12}+\dfrac{5}{21}\)

\(=1-\dfrac{13}{12}=-\dfrac{1}{12}\)

6: \(\left(\dfrac{13}{23}+\dfrac{-15}{4}\right)+\left(\dfrac{10}{23}-\dfrac{1}{4}\right)\)

\(=\dfrac{13}{23}+\dfrac{10}{23}-\dfrac{15}{4}-\dfrac{1}{4}\)

\(=1-4=-3\)

Bài 18:

1: \(6\dfrac{2}{5}-\left(2\dfrac{4}{9}+4\dfrac{2}{5}\right)\)

\(=6+\dfrac{2}{5}-2-\dfrac{4}{9}-4-\dfrac{2}{5}\)

\(=-\dfrac{4}{9}\)

2: \(7\dfrac{3}{5}-\left(2\dfrac{5}{7}+5\dfrac{3}{5}\right)\)

\(=7+\dfrac{3}{5}-2-\dfrac{5}{7}-5-\dfrac{3}{5}\)

\(=-\dfrac{5}{7}\)

3: \(8\dfrac{2}{7}-\left(3\dfrac{4}{9}+4\dfrac{2}{7}\right)\)

\(=8+\dfrac{2}{7}-3-\dfrac{4}{9}-4-\dfrac{2}{7}\)

\(=1-\dfrac{4}{9}=\dfrac{5}{9}\)

4: \(8\dfrac{2}{9}-\left(4\dfrac{2}{9}-5\dfrac{1}{2}\right)\)

\(=8+\dfrac{2}{9}-4-\dfrac{2}{9}+5+\dfrac{1}{2}\)

\(=9+\dfrac{1}{2}=\dfrac{19}{2}\)

5: \(21\dfrac{4}{11}-\left(1\dfrac{3}{5}+7\dfrac{4}{11}\right)\)

\(=21+\dfrac{4}{11}-1-\dfrac{3}{5}-7-\dfrac{4}{11}\)

\(=13-\dfrac{3}{5}=\dfrac{62}{5}\)

6: \(11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)

\(=11+\dfrac{3}{13}-2-\dfrac{4}{7}-5-\dfrac{3}{13}\)

\(=4-\dfrac{4}{7}=\dfrac{24}{7}\)

7: \(\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)

\(=6+\dfrac{4}{9}+3+\dfrac{7}{11}-4-\dfrac{4}{9}\)

\(=5+\dfrac{7}{11}=\dfrac{62}{11}\)

8: \(\left(7\dfrac{8}{9}+2\dfrac{3}{13}\right)-4\dfrac{8}{9}\)

\(=7+\dfrac{8}{9}+2+\dfrac{3}{13}-4-\dfrac{8}{9}\)

\(=5+\dfrac{3}{13}=\dfrac{68}{13}\)

9: \(\left(6\dfrac{5}{7}+2\dfrac{7}{9}\right)-4\dfrac{5}{7}\)

\(=6+\dfrac{5}{7}+2+\dfrac{7}{9}-4-\dfrac{5}{7}\)

\(=4+\dfrac{7}{9}=\dfrac{43}{9}\)

                         Bài 3:

          1; A = 1 + 2 + 3 + ... + 2023 + 2024

   Dãy số trên là dãy số cách đều với khoảng cách là:  2 - 1 = 1

   Số số hạng của dãy số trên là: (2024 - 1) : 1 + 1 = 2024

  Tổng của dãy số trên là: (2024 + 1) x 2024 : 2  =  2049300

   Đáp số:....

                 BÀi 3:

2; B = 1 + 3 + 5 + ... + 2023 + 2025

   Xét dãy số: 1; 3; 5;...; 2023; 2025

Dãy số trên là dãy số cách đều với khoảng cách là:

                3 - 1 = 2

Số số hạng của dãy số trên là: (2025 - 1) : 2 + 1 =  1013

Tổng của dãy số trên là: (2025 + 1) x 1013 : 2 = 1026196

`#3107.101107`

- Các số trong tập hợp cách nhau `5` đơn vị

Số phần tử của tập hợp X:

\(\left(277-2\right)\div5+1=56\) (phần tử)

Vậy, số phần tử của tập hợp X là `56.`

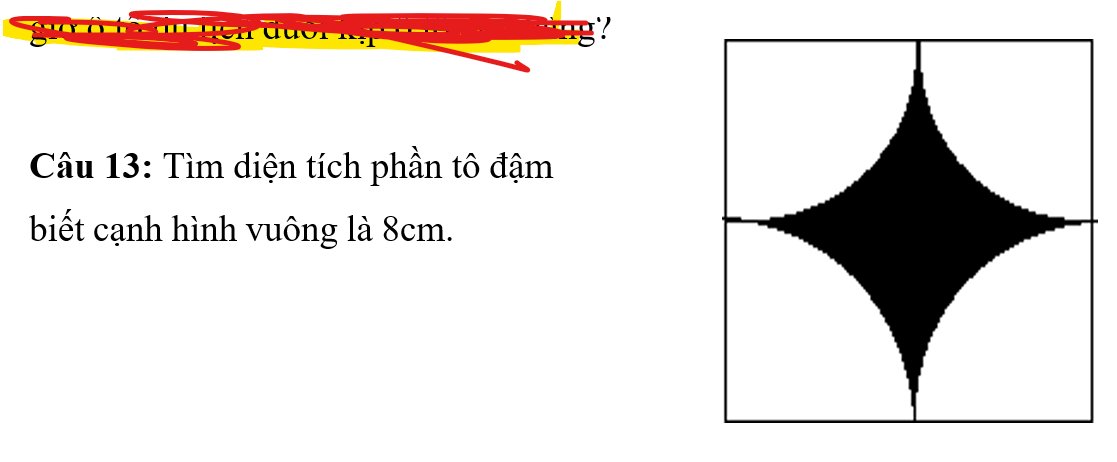
Diện tích cả hình là: 

\(8\times8=64\left(cm^2\right)\)

Bán kính của mỗi `1/4` hình tròn là: 

\(8\times\dfrac{1}{2}=4\left(cm\right)\)

Diện tích phần màu trắng là:

\(4\times\left(\dfrac{1}{4}\times4\times4\times3,14\right)=50,24\left(cm^2\right)\)

Diện tích phần tô đậm là:

\(64-50,24=13,76\left(cm^2\right)\)

ĐS: ...

\(\left(x-\dfrac{2}{7}\right)^5=32\\ =>\left(x-\dfrac{2}{7}\right)^5=2^5\\ =>x-\dfrac{2}{7}=2\\ =>x=\dfrac{2}{7}+2\\ =>x=\dfrac{16}{7}\)

\(\left(x+\dfrac{4}{3}\right)^4=\dfrac{1}{81}\\ =>\left(x+\dfrac{4}{3}\right)^4=\left(\dfrac{1}{3}\right)^4\)

TH1: `x+4/3=1/3`

`=>x=1/3-4/3`

`=>x=-3/3`

`=>x=-1`

TH2: `x+4/3=-1/3`

`=>x=-1/3-4/3`

`=>x=-5/3`

Vậy: ...

\(\overline{abc4}-\overline{abc}-1111\\ \overline{abc}\cdot10+4-\overline{abc}=1111\\ \overline{abc}\cdot\left(10-1\right)=1111-4\\ \overline{abc}\cdot9=1107\\ \overline{abc}=1107:9\\ \overline{abc}=123\) 

_____________________

\(\overline{ab5}=\overline{ab}+230\\ \overline{ab}\cdot10+5=\overline{ab}+230\\ \overline{ab}\cdot10-\overline{ab}=230-5\\ =>\overline{ab}\cdot\left(10-1\right)=225\\ =>\overline{ab}\cdot9=225\\ =>\overline{ab}=225:9\\ =>\overline{ab}=25\)