Bài 3. (1,0 điểm) Trong một hộp có $20$ thẻ gồm $4$ thẻ được đánh số 1, $4$ thẻ được đánh số 2, $6$ thẻ được đánh số 3, $3$ thẻ được đánh số 4 và $3$ thẻ được đánh số 5. Tính xác suất cho biến cố “Thẻ rút ra là thẻ đánh số 3”.h số 2, $6$ thẻ được đánh số 3, $3$ thẻ được đánh số 4 và $3$ thẻ được đánh số 5. Tính xác suất cho biến cố “Thẻ rút ra là thẻ đánh số 3”.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Đổi 1 giờ 30 phút = 1,5 giờ
Cứ một giờ ca nô xuôi dòng được: 1 : 1,5 = \(\dfrac{2}{3}\)(quãng sông AB)
Cứ một giờ ca nô ngược dòng được: 1 : 2 = \(\dfrac{1}{2}\) (quãng sông AB)
Cứ một giờ dòng nước chảy được: (\(\dfrac{2}{3}\) - \(\dfrac{1}{2}\)) : 2 = \(\dfrac{1}{12}\)(quãng sông AB)
Quãng sông AB dài là: 3 : \(\dfrac{1}{12}\) = 36 (km)
Vận tốc ca nô khi ngược dòng là: 36 : 2 = 18 (km/h)
Vận tốc riêng của ca nô là: 18 + 3 = 21 (km/h)
Kết luận: Quãng sông AB dài 36 km
Vận tốc riêng của ca nô là 21 km/h
Gọi x (km/h) là vận tốc riêng của ca nô (x > 3)
Vận tốc đi xuôi dòng từ A đến B: x + 3 (km/h)
1 giờ 30 phút = 1,5 giờ
Quãng đường đi xuôi dòng: (x + 3).1,5 (km)
Vận tốc đi ngược dòng từ B về A: x - 3 (km/h)
Quãng đường đi ngược dòng: (x - 3).2 (km)
Do đi cùng một quãng đường AB nên ta có phương trình:
(x + 3).1,5 = (x - 3).2
1,5x + 4,5 = 2x - 6
2x - 1,5x = 4,5 + 6
0,5x = 10,5
x = 10,5 : 0,5
x = 21 (nhận)
Vậy vận tốc riêng của ca nô là 21 km/h

a) 3x - 4 = 5 + x
3x - 2x = 5 + 4
x = 9
Vậy S = {9}
b) 3(x - 1) - 7 = 5(x + 2)
3x - 3 - 7 = 5x + 10
3x - 10 = 5x + 10
3x - 5x = 10 + 10
-2x = 20
x = 20 : (-2)
x = -10
Vậy S = {-10}

(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c
a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab
ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab
(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab
(a + b + c)x = (a + b + c)²
x = (a + b + c)²/(a + b + c)
x = a + b + c
Vậy S = {a + b + c}
Ta có:
Điều kiện xác định:
Khi đó:
+ Nếu thì phương trình có vô số nghiệm.
+ Nếu thì phương trình có nghiệm duy nhất .

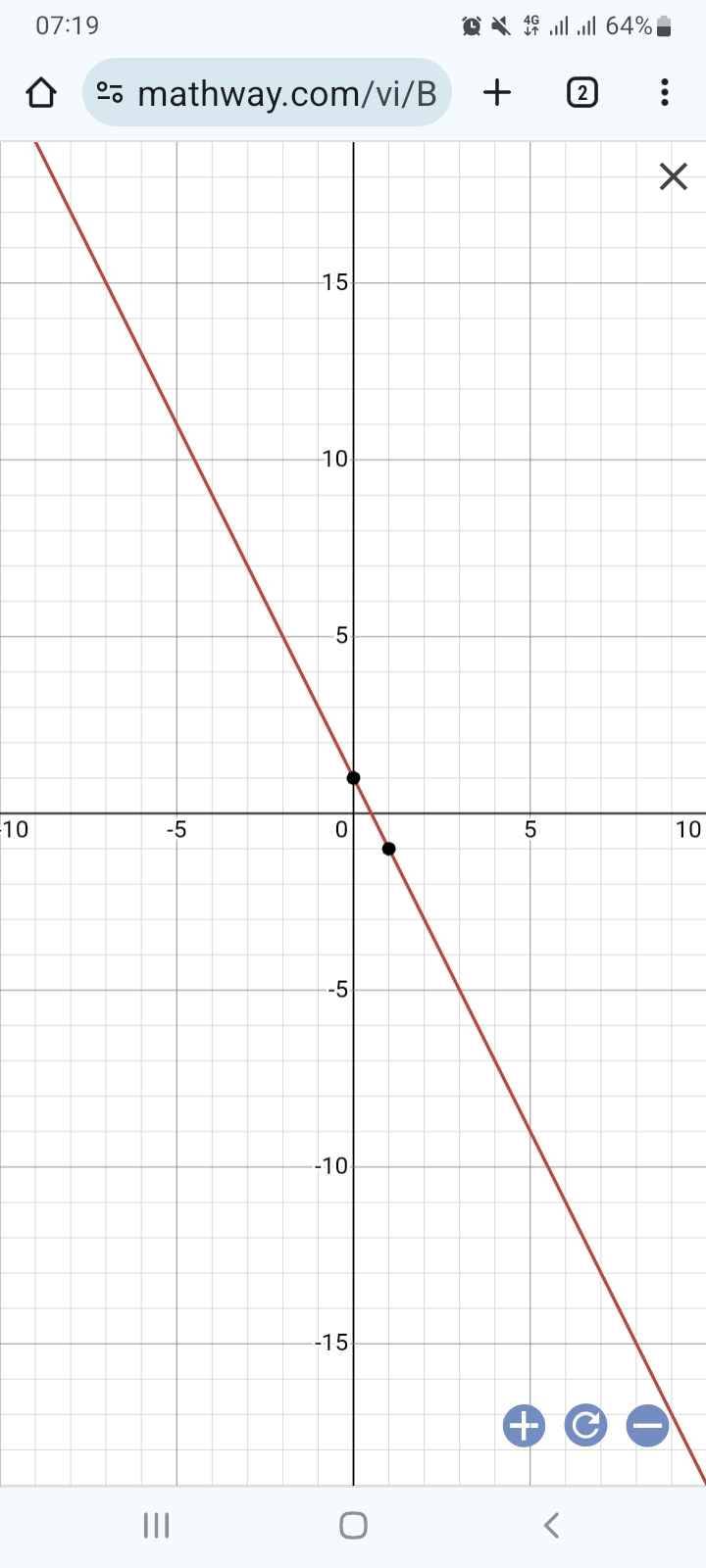
a) Với , hàm số trở thành .
Xét hàm số :
Thay thì .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Thay thì .
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .
Suy ra đồ thị hàm số đi qua điểm có tọa độ .
Vẽ đồ thị:
Vì đường thẳng song song với đường thẳng nên: .
Khi đó ta có: và .
Vì đường thẳng đi qua nên:
Suy ra (thoả mãn)
Vậy đường thẳng cần tìm là .

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)
20 phút = 1/3 h
Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)
Quãng đường đi từ thành phố về quê: 30x (km)
Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)
Theo đề bài, ta có phương trình:
30x = 25(x + 1/3)
30x = 25x + 25/3
30x - 25x = 25/3
5x = 25/3
x = 25/3 : 5
x = 5/3 (nhận)
Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) 3x - 5 = 4
3x = 4 + 5
3x = 9
x = 9 : 3
x = 3
Vậy S = {3}
b) 2x/3 + (3x - 1)/6 = x/2
4x + 3x - 1 = 3x
7x - 3x = 1
4x = 1
x = 1/4
Vậy S = {1/4}

a: Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=90^0\)
=>\(\widehat{IBC}+\widehat{ICB}=45^0\)
Xét ΔBIC có \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)
=>\(\widehat{BIC}+45^0=180^0\)
=>\(\widehat{BIC}=135^0\)

2a/
$(2x+1)^2(x-1)(x+2)=100$
$\Leftrightarrow (4x^2+4x+1)(x^2+x-2)=100$
Đặt $x^2+x=a$ thì PT trở thành:
$(4a+1)(a-2)=100$
$\Leftrightarrow 4a^2-8a+a-2=100$
$\Leftrightarrow 4a^2-7a-102=0$
$\Leftrightarrow (a-6)(4a+17)=0$
$\Leftrightarrow a-6=0$ hoặc $4a+17=0$
Nếu $a-6=0$
$\Leftrightarrow x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
Nếu $4a+17=0$
$\Leftrightarrow 4x^2+4x+17=0$
$\Leftrightarrow (2x+1)^2=-16<0$ (vô lý)
Vậy PT có nghiệm $x=2$ hoặc $x=-3$
2b/
\(\frac{b-c}{(a-b)(a-c)}+\frac{c-a}{(b-c)(b-a)}+\frac{a-b}{(c-a)(c-b)}=\frac{(a-c)-(a-b)}{(a-b)(a-c)}+\frac{(b-a)-(b-c)}{(b-c)(b-a)}+\frac{(c-b)-(c-a)}{(c-a)(c-b)}\\ =\frac{1}{a-b}-\frac{1}{a-c}+\frac{1}{b-c}-\frac{1}{b-a}+\frac{1}{c-a}-\frac{1}{c-b}\\ =\frac{1}{a-b}+\frac{1}{c-a}+\frac{1}{b-c}+\frac{1}{a-b}+\frac{1}{c-a}+\frac{1}{b-c}\\ =\frac{2}{a-b}+\frac{2}{b-c}+\frac{2}{c-a}\)
Ta có đpcm.








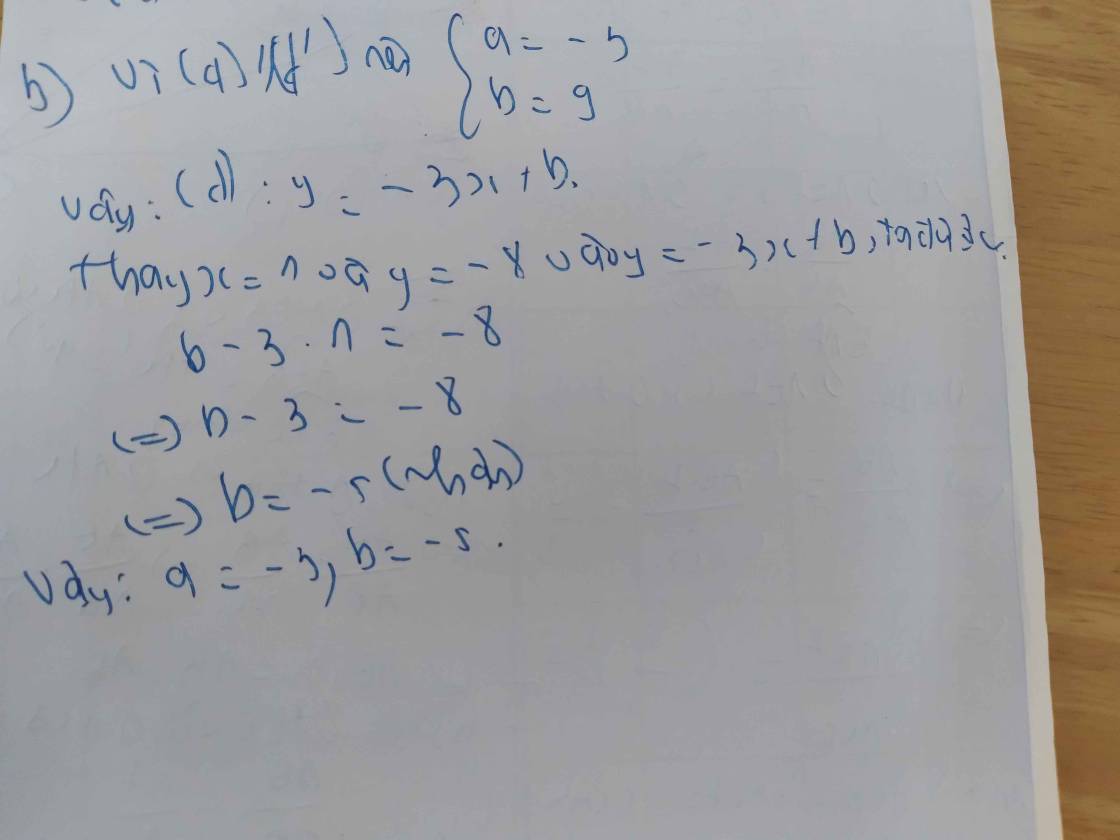

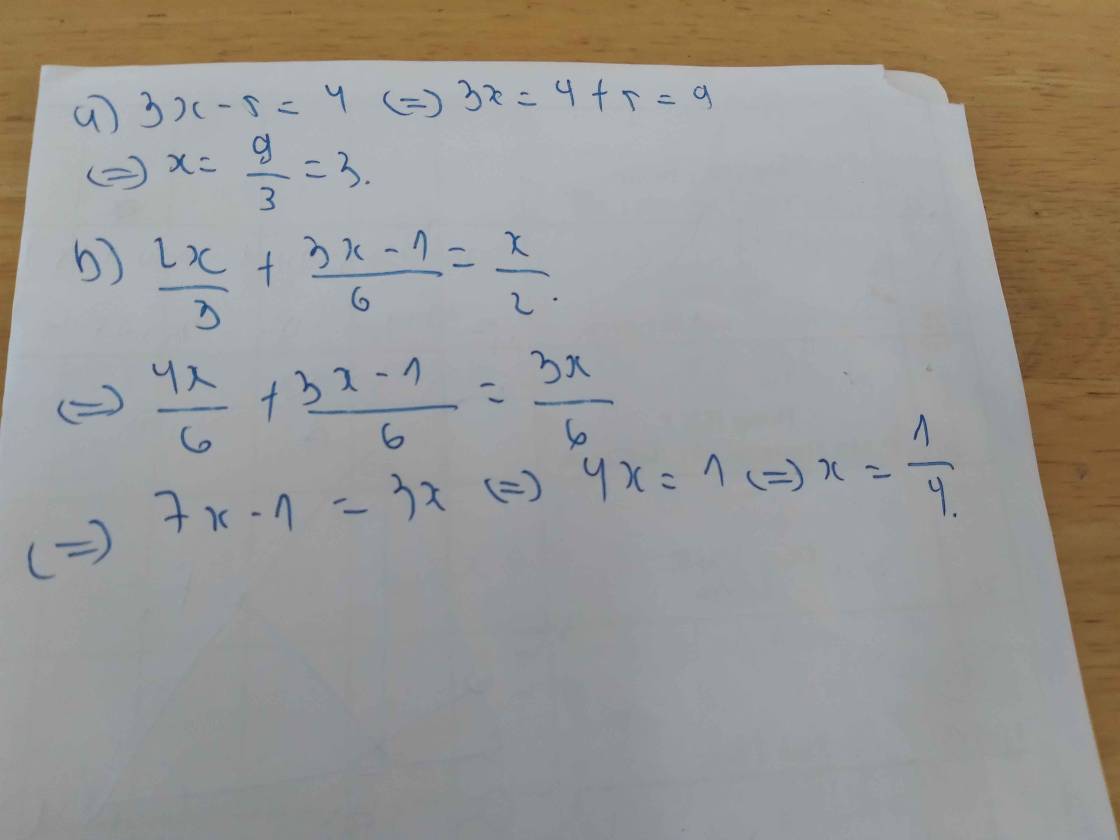

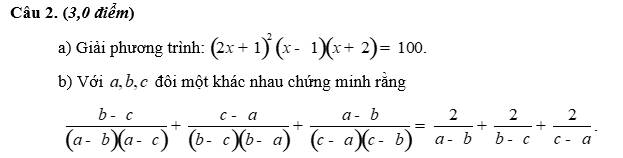
Có 6 khả năng rút được thẻ số 3 nên xác suất của biến cố "Thẻ rút ra là thẻ đánh số 3" là:
P = 6/20 = 3/10