Thay biểu thức này vào phương trình a + b + c = abc, ta được a + ac + c = ac^2.

Sắp xếp lại, ta có (a - ac)(1 - c) = 0.

Vì a > 0 nên (1 - c) phải bằng 0, từ đó suy ra c = 1.

Thay c = 1 vào biểu thức ac = b, ta được a * 1 = b hay b = a.

Vậy, để a đạt giá trị nhỏ nhất thì b và c phải thoả mãn điều kiện là b=c=1.

Xét (O) có

\(\widehat{CBD}\) là góc nội tiếp chắn cung CD

\(\widehat{CED}\) là góc nội tiếp chắn cung CD

Do đó: \(\widehat{CBD}=\widehat{CED}\)

Xét ΔNEC và ΔNBD có

\(\widehat{NEC}=\widehat{NBD}\)

\(\widehat{ENC}=\widehat{BND}\)(hai góc đối đỉnh)

Do đó: ΔNEC~ΔNBD

5/9+13/7+15/3+8/7+4/9+11/3=?

giúp mình với mình đang cần rất gấp.Làm ơn.

5/9+13/7+15/3+8/7+4/9+11/3=38/3

tự giải

    

a: Xét (I) có

ΔBEH nội tiếp

BH là đường kính

Do đó: ΔBEH vuông tại E

=>HE\(\perp\)AB tại E

Xét (K) có

ΔCFH nội tiếp

CH là đường kính

Do đó: ΔCFH vuông tại F

=>HF\(\perp\)AC tại F

Xét tứ giác AEHF có

\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)

nên AEHF là hình chữ nhật

ΔABC vuông cân tại A

mà AH là đường cao

nên AH là đường phân giác của góc BAC và H là trung điểm của BC

Hình chữ nhật AEHF có AH là đường phân giác của góc FAE

nên AEHF là hình vuông

b: Ta có: AEHF là hình chữ nhật

=>\(\widehat{AEF}=\widehat{AHF}\)

mà \(\widehat{AHF}=\widehat{ACB}\left(=90^0-\widehat{HAC}\right)\)

nên \(\widehat{AEF}=\widehat{ACB}\)

=>\(\widehat{FEB}+\widehat{FCB}=180^0\)

=>BEFC là tứ giác nội tiếp

c: Xét ΔAHB vuông tại H có HE là đường cao

nên \(AE\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HF là đường cao

nên \(AF\cdot AC=AH^2\left(2\right)\)

Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)

e: Ta có: ΔABC vuông tại A

mà AH là đường trung tuyến

nên HA=HB=HC

=>ΔABC nội tiếp (H)

Xét (H) có

AH là bán kính

Ax là tiếp tuyến tại A

Do đó: AH\(\perp\)Ax

mà AH\(\perp\)FE(AEHF là hình vuông)

nên Ax//FE

 Đúng(0)   Những câu hỏi liên quan Vũ Hạ Nguyên19 tháng 3 2017 lúc 11:35  

Cho tam giác ABC vuông tại A, biết AB=6cm, AC= 8cm, vẽ đường cao AH, đường tròn tâm O, đường kính AH cắt AB tại E, AC tại F. C/m tứ giác BEFC nội tiếp

#Toán lớp 9    0       Pham Trong Bach24 tháng 8 2019 lúc 7:03   Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (O) đường kính BH và đường tròn tâm O' đường kính CH, hai đường tròn này cắt AB, AC thứ tự tại E và Fa, Tứ giác AEHF là hình gì?b, Chứng minh EF là tiếp tuyến chung của (O) và (O’)c, Chứng minh đường tròn đường kính OO' tiếp xúc với EFd, Cho đường tròn tâm I bán kính r tiếp xúc với EF, (O) và (O’). Tính r theo BH và... Đọc tiếp #Toán lớp 9    1     Cao Minh Tâm 24 tháng 8 2019 lúc 7:04  

a, HS tự làm

b, HS tự làm

c, Chú ý hình thang vuông OEFO’ và xét đường trung bình của hình thang này

d, Từ I kẻ đường thảng song song với EF cắt OE tại M , cắt O’F tại N

Đặt BH=2R; CH= 2R’

∆IOM vuông tại M có:

I M 2 = I O 2 - O M 2 =  R + r 2 - R - r 2 = 4 R r

Tương tự , ∆ION có  I N 2 = 4 R ' r

Suy ra IM+IN=EF=AH

Vậy  2 R r + 2 R ' r = 2 R R '

=>  r R + R ' = R R '

=> r =  R R ' R + R ' 2

 Đúng(0)   Nguyễn Quang Huy14 tháng 1 2023 lúc 22:37   Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I đường kính BH, cắt AB ở M. Vẽ đường tròn tâm K có đường kính CH , cắt AC ở Na) Tứ giác AMHN là hình gì ?b) Chứng minh tăng MN là tiếp tuyến chung của hai đường tròn (I) và (K)c) Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR Ax//MN #Toán lớp 9    1     Nguyễn Lê Phước Thịnh 14 tháng 1 2023 lúc 22:53  

a: Xét (I) có

ΔHMB nội tiếp

HB là đường kính

Do đó: ΔHMB vuông tại M

Xét (K) có

ΔCNH nội tiếp

CH là đường kính

=>ΔCNH vuông tại N

Xét tứ giác AMHN có

góc AMH=góc ANH=góc MAN=90 độ

nên AMHN là hình chữ nhật

b: góc NMI=góc NMH+góc IMH

=góc NAH+góc IHM

=góc CAH+góc HCA=90 độ

=>NM là tiếp tuyến của (I)

góc KNM=góc KNH+góc MNH

=góc KHN+góc MAH

=góc BAH+góc B=90 độ

=>MN là tiếp tuyến của (K)

 Đúng(0)   Trọng Nhân Mã16 tháng 9 2021 lúc 19:25   Cho tam giác ABC vuông tại A, ∠ABC = 60◦, AB = a.a) Xác định tâm O và tính bán kính đường tròn ngoại tiếp tam giác ABC.b) Vẽ đường cao AH. Đường tròn đường kính BH cắt AB tại D và đường tròn đườngkính CH cắt AC tại E. Tứ giác ADHE là hình gì? Tính DE.c) Chứng minh rằng... Đọc tiếp #Toán lớp 9    1     Nguyễn Lê Phước Thịnh 16 tháng 9 2021 lúc 21:57  

a: O là trung điểm của BC

b: Xét (��2)(2BH​) có

ΔBDH là tam giác nội tiếp

BH là đường kính

Do đó: ΔBDH vuông tại D

Xét (��2)(2CH​)có

ΔCHE nội tiếp đường tròn

CH là đường kính

Do đó: ΔCHE vuông tại E

Xét tứ giác ADHE có 

���^=���^=���^=900AEH=ADH=EAD=900

Do đó: ADHE là hình chữ nhật

 Đúng(0)   Nguyễn Vũ Mỹ An 18 tháng 9 2021 lúc 10:10  

tính bán kính đường tròn ngoại tiếp làm sao ạ?

 Đúng(0)   Toán Hình THCS5 tháng 6 2019 lúc 8:12  

cho tam giác ABC vuông tại A ( ab<ac)  đường cao AH . Trên nửa mạt phẳng bờ BC chứa A vẽ nửa đường tròn đường kính BH cắt AB tại E và nửa đường tròn đường kính CH cắt AC tại F . CMR:

a, tứ giác AEHF là hình chữ nhạt

b, EF là tiếp tuyến chung của 2 đg tròn đường kính BH và CH 

c, tứ giác BCFE nội tiếp

ko cầnvẽ hình nha

#Toán lớp 9    2     Aug.21 5 tháng 6 2019 lúc 8:26  

a, Ta có : ���^=���^=1�HEB=HFC=1v( góc nội tiếp chắn nửa đường tròn )

⇒���^=���^=���^=1�⇒HEA=HFA=EAF=1v

$\Rightarrow$Tứ giác AEHF là hình chữ nhật

b, Gọi O và O' lần lượt là trung điểm của HB và HC .

Ta có O là trung tâm đường tròn đường kính HB và O' là tâm dường tròn đường kính HC

⇒���^=���^⇒HEO=EHO( Tam giác EHO cân)

     ���^=���^FEH=FHE ( Tam giác IHE cân )

⇒���^+���^=���^+���^=900⇒��⊥��⇒FEH+HEO=FHE+EHO=900⇒OE⊥EF

Vậy EF là tiếp tuyến của đường tròn (O)

Chứng minh tương tự ta có EF là tiếp tuyến của đường tròn (O')

c, Ta có: ���^=���^EBC=FAH( góc nhọn có cạnh tương ứng vuông góc)

               ���^=���^FAH=AFE( Tam giác AIF cân )

⇒���^=���^⇒EBC=AFEmà ���^+���^=2�AFE+EFC=2v( Kề bù)

⇒���^+���^=2�⇒EBC+EFC=2v

Vậy tứ giác BCFE nội tiếp.

 Đúng(0)   ๖ۣۜNɦσƙ ๖ۣۜTì 5 tháng 6 2019 lúc 8:17  

a. Ta có : ÐBEH = 900 ( nội tiếp chắn nửc đường tròn )

=> ÐAEH = 900 (vì là hai góc kề bù). (1)

ÐCFH = 900 ( nội tiếp chắn nửc đường tròn )

=> ÐAFH = 900 (vì là hai góc kề bù).(2)

ÐEAF = 900 ( Vì tam giác  ABC vuông tại A) (3)

Từ (1), (2), (3) => tứ giác AFHE là hình chữ nhật ( vì có ba góc vuông).

b.Tứ giác AFHE là hình chữ nhật => IE = EH => DIEH cân tại I => ÐE1 = ÐH1 .

DO1EH cân tại O1 (vì có O1E vàO1H cùng là bán kính) => ÐE2 = ÐH2.

=> ÐE1 + ÐE2 = ÐH1 + ÐH2 mà ÐH1 + ÐH2 = ÐAHB = 900 => ÐE1 + ÐE2 = ÐO1EF = 900

=> O1E ^EF .

Chứng minh tương tự ta còng có O2F ^ EF. Vậy EF là tiếp tuyến chung của hai nửa đường tròn  .

c.  Tứ giác AFHE là hình chữ nhật nên nội tiếp được một đường tròn =>ÐF1=ÐH1 (nội tiếp chắn cung AE) . Theo giả thiết AH ^BC nên AH là tiếp tuyến chung của hai nửa đường tròn  (O1) và (O2)     

 => ÐB1 = ÐH1 (hai góc nội tiếp cùng chắn cung HE) => ÐB1= ÐF1 => ÐEBC+ÐEFC = ÐAFE + ÐEFC màÐAFE + ÐEFC = 1800 (vì là hai góc kề bù) => ÐEBC+ÐEFC = 1800  mặt khác ÐEBC và ÐEFC là hai góc đối của tứ giác BEFC do đó BEFC là tứ giác nội tiếp.

 Đúng(0)   Xem thêm câu trả lời ARMY MINH NGỌC15 tháng 7 2017 lúc 6:58  

Cho tam giác ABC vuông tại A, đường cao AH, vẽ đường tròn tâm I đươngf kính BH cắt AB tại D.Vẽ đường tròn tâm K đường kính CH cắt AC tại E. CMR:

a, AD.AB=AE.AC

b,DE là tiếp tuyến chung của đường tròn tâm I và tâm K

#Toán lớp 9    0       Dương quốc thế19 tháng 5 2018 lúc 18:13  

Cho tam giác ABC vuông ở A( AB>AC), đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A, vẽ nữa đường tròn đường kính BH cắt AB tại E, nửa đường tròn đường kính HC cắt AC tại F. Chứng minh:a, Tứ giác AFHE là hình chữ nhật. b, tứ giác BEFC là tứ giác nội tiếp đường tròn. c, EF là tiếp tuyến chung của 2 nửa đường tròn đường kính BH và HC

#Toán lớp 9    3     Anh 19 tháng 5 2018 lúc 18:43  

a, ta có : góc CFH=90°; góc HEB=90°(góc nội tiếp chắn 1/2đtròn)

xét tứ giác AEHF có góc A=gócE=góc F=90°

suy ra AEHF là hcn.

b, vì AEHF là hcn suy ra AEHF nội tiếp suy ra góc AFE=AHE( góc nội tiếp chắn cung AE) (1)

ta lại có: góc AHE=ABH(cùng bù với BAH) (2)

từ 1 và 2 suy ra góc AFE=ABH

mà góc CFE+AFE=180°

suy ra góc CFE+ABH=180°

suy ra BEFC nội tiếp

c, gọi I và K lần lượt là tâm đtròn đường kính HB và HC

gọi O là giao điểm AH và EF

vì AEHF là hcn suy ra OF=OH suy ra tam giác FOH cân tại O

suy ra góc OFH=OHF

vì CFH vuông tại F suy ra KC=KF=KH

suy ra tam giác HKF cân tại K

suy ra góc KFH=KHF

mà góc KHF+FHA=90°

suy ra góc KFH+HFO=90°

suy ra EF là tiếp tuyến của đtròn tâm K

tương tự EF là tiếp tuyến đường tròn tâm I

vậy EF là tiếp tuyến chung của hai nửa đường tròn đường kính HB và HC

 Đúng(0)   ๖ۣۜNɦσƙ ๖ۣۜTì 5 tháng 6 2019 lúc 8:35  

a)

1. Ta có : ÐBEH = 900 ( nội tiếp chắn nửc đường tròn )

=> ÐAEH = 900 (vì là hai góc kề bù). (1)

ÐCFH = 900 ( nội tiếp chắn nửc đường tròn )

=> ÐAFH = 900 (vì là hai góc kề bù).(2)

ÐEAF = 900 ( Vì tam giác  ABC vuông tại A) (3)

Từ (1), (2), (3) => tứ giác AFHE là hình chữ nhật ( vì có ba góc vuông)

b)  Tứ giác AFHE là hình chữ nhật nên nội tiếp được một đường tròn

=>ÐF1=ÐH1 (nội tiếp chắn cung AE) .

Theo giả thiết AH ^BC nên AH là tiếp tuyến chung của hai nửa đường tròn  (O1) và (O2)     

 => ÐB1 = ÐH1 (hai góc nội tiếp cùng chắn cung HE) => ÐB1= ÐF1 => ÐEBC+ÐEFC = ÐAFE + ÐEFC màÐAFE + ÐEFC = 1800 (vì là hai góc kề bù) => ÐEBC+ÐEFC = 1800  mặt khác ÐEBC và ÐEFC là hai góc đối của tứ giác BEFC do đó BEFC là tứ giác nội tiếp.

c)

Tứ giác AFHE là hình chữ nhật => IE = EH => DIEH cân tại I => ÐE1 = ÐH1 .

DO1EH cân tại O1 (vì có O1E vàO1H cùng là bán kính) => ÐE2 = ÐH2.

=> ÐE1 + ÐE2 = ÐH1 + ÐH2 mà ÐH1 + ÐH2 = ÐAHB = 900 => ÐE1 + ÐE2 = ÐO1EF = 900

=> O1E ^EF .

Chứng minh tương tự ta còng có O2F ^ EF. Vậy EF là tiếp tuyến chung của hai nửa đường tròndường kính BH và HC.

 Đúng(0)   Xem thêm câu trả lời Giang Nguyễn23 tháng 12 2022 lúc 13:49   Cho tam giác ABc vuông tại A đường cao AH vẽ đường tròn tâm I đường kính BH cắt AB tại M và đường tròn tâm K đường kính CH cắt AC tại Na Chứng minh rằng tứ giác AMHN là hình chữ nhậtb Chứng minh rằng MN là tiếp tuyến chung của hai đường trònc Tìm điều kiện của tam giác ABC để M N có độ dài lớn... Đọc tiếp #Toán lớp 9    1     Nguyễn Lê Phước Thịnh 12 tháng 1 2023 lúc 9:14  

a: Xét (I) có

ΔHMB nội tiếp

HB là đường kính

Do đó: ΔHMB vuông tại M

Xét (K) có

ΔCNH nội tiếp

HC là đường kính

Do đó; ΔCNH vuông tại N

Xét tứ giác AMHN có

góc AMH=góc ANH=góc MAN=90 độ

nên AMHN là hình chữ nhật

b: góc IMN=góc IMH+góc NMH

=góc IHM+góc NAH

=góc HAC+góc HCA=90 độ

=>NM là tiếp tuyến của (I)

góc KNM=góc KNH+góc MNH

=góc KHN+góc MAH

=góc HBA+góc HAB=90 độ

=>MN là tiếp tuyến của (K)

 Đúng(0)   chanh19 tháng 5 2022 lúc 22:00   ai giúp e vs ạahuhuhc4cho tam giác ABC vuông A (AB>AC), đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A, vẽ nửa đường tròn đường ính BH cắt AB tại E, nửa đg tròn đg kính HC cắt AC tại F. CMRa/ tức giác AFHE là hình chữ nhậtb/ tứ giác BEFC nội tiếpc/ EF là tiếp tuyến chung của 2 nửa đg tròn đg kính BH và... Đọc tiếp #Toán lớp 9    1     Nguyễn Lê Phước Thịnh 14 tháng 6 2023 lúc 0:46  

a: góc HEB=1/2*180=90 độ

=>HE vuông góc AB

góc CFH=1/2*180=90 độ

=>HF vuông góc AC

góc AEH=góc AFH=góc FAE=90 độ

=>AEHF là hcn

b: góc AEF=góc AHF=góc C

=>góc FEB+góc C=180 độ

=>FEBC nội tiếp

c: gọi I,K lần lượt là trung điểm của BH,CH

góc IEF=góc IEH+góc FEH

=góc IHE+góc FAH

=góc HAC+góc HCA=90 độ

=>FE là tiếp tuyến của (I)

góc KFE=góc KFH+góc EFH

=góc KHF+góc EAH

=góc HAB+góc HBA=90 độ

=>EF là tiếp tuyến của (K)

 Đúng(0)   chanh19 tháng 5 2022 lúc 20:32   ai giúp e vs ạahuhuhc4cho tam giác ABC vuông A (AB>AC), đường cao AH. Trên nửa mặt phẳng bờ BC chứa điểm A, vẽ nửa đường tròn đường ính BH cắt AB tại E, nửa đg tròn đg kính HC cắt AC tại F. CMRa/ tức giác AFHE là hình chữ nhậtb/ tứ giác BEFC nội tiếpc/ EF là tiếp tuyến chung của 2 nửa đg tròn đg kính BH và... Đọc tiếp #Toán lớp 9    1     chanh 19 tháng 5 2022 lúc 20:35  

huhu mmn oi

 Đúng(0)   Xếp hạng 

• Tuần
• Tháng
• Năm

• Nguyễn Lê Phước Thịnh 30 GP
• Kiều Vũ Linh 28 GP
• Thanh Phong (9A5) 23 GP
• 789000 15 GP
• Trần Nguyễn Phương Thảo VIP 10 GP
• Toru 7 GP
• Nguyễn Đức Huy 7 GP
• Coin Hunter 5 GP
• Bình Minh 3 GP
• Nguyễn Minh Khuê VIP 3 GP
•  

   

a: Xét tứ giác  MAOB có 

\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{MAF}\) là góc tạo bởi tiếp tuyến AM và dây cung AF

\(\widehat{AEF}\) là góc nội tiếp chắn cung AF

Do đó: \(\widehat{MAF}=\widehat{AEF}\)

mà \(\widehat{AEF}=\widehat{NMF}\)(hai góc so le trong, MN//AE)

nên \(\widehat{NMF}=\widehat{NAM}\)

Xét ΔNMF và ΔNAM có

\(\widehat{NMF}=\widehat{NAM}\)

\(\widehat{MNF}\) chung

Do đó: ΔNMF~ΔNAM

=>\(\dfrac{NM}{NA}=\dfrac{NF}{NM}\)

=>\(NM^2=NF\cdot NA\)

Gọi số học sinh của lớp 9A và lớp 9B lần lượt là x(bạn) và y(bạn)

(Điều kiện: \(x,y\in Z^+\))

Số khẩu trang y tế lớp 9A nhận được là 2x(cái)

Số khẩu trang vải lớp 9A nhận được là 3x(cái)

Số khẩu trang y tế lớp 9B nhận được là y*1=y(cái)

Số khẩu trang vải lớp 9B nhận được là 4y(cái)

Tổng số khẩu trang là 360 nên 2x+3x+y+4y=360

=>5x+5y=360

=>x+y=72(1)

Số khẩu trang vải nhiều hơn số khẩu trang y tế là 146 nên 

4y+3x-2x-y=146

=>x+3y=146(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=72\\x+3y=146\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=72-146=-74\\x+y=72\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=37\\x=72-37=35\end{matrix}\right.\left(nhận\right)\)

Vậy: số học sinh của lớp 9A và lớp 9B lần lượt là 35 bạn và 37 bạn 

Câu 3:

a: 

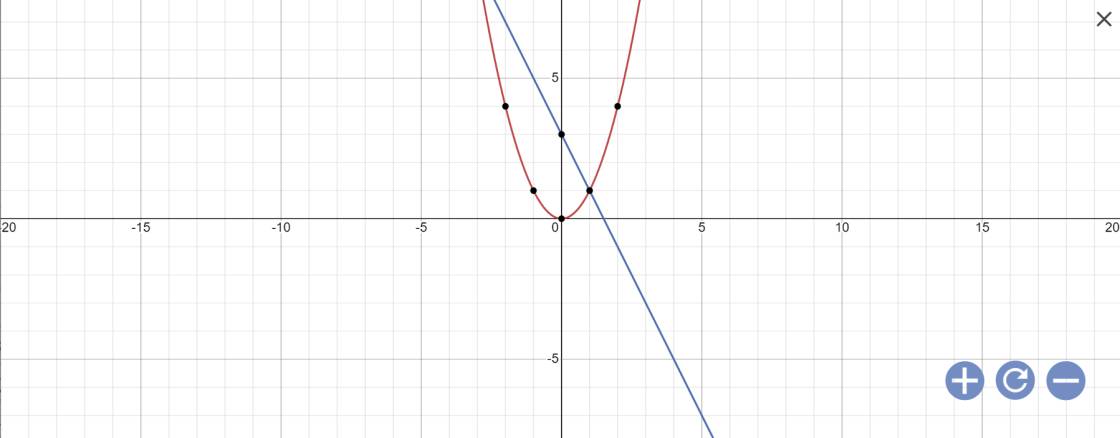
b: Phương trình hoành độ giao điểm là:

\(x^2=-2x+3\)

=>\(x^2+2x-3=0\)

=>(x+3)(x-1)=0

=>\(\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

Khi x=-3 thì \(y=\left(-3\right)^2=9\)

Khi x=1 thì \(y=1^2=1\)

Vậy: (P) cắt (d) tại A(-3;9); B(1;1)

Câu 4:

a:

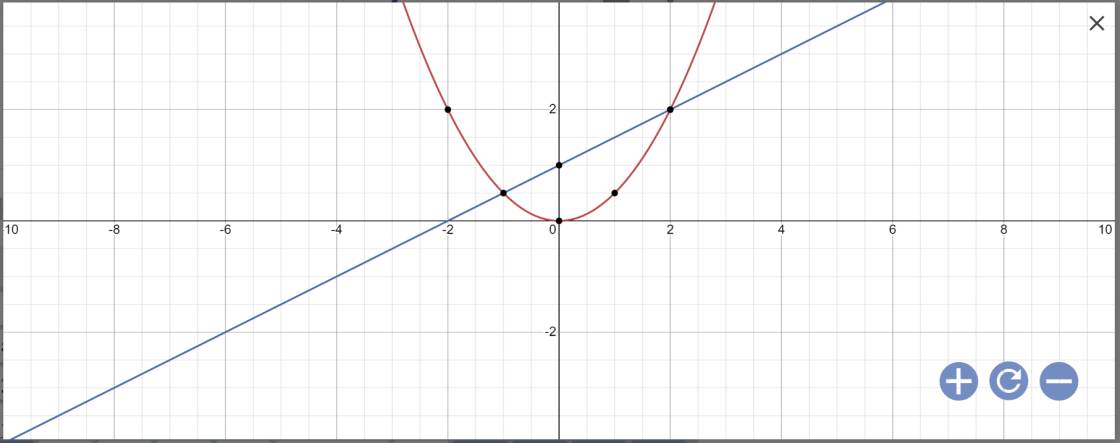
b: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=\dfrac{1}{2}x+1\)

=>\(x^2=x+2\)

=>\(x^2-x-2=0\)

=>(x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

Khi x=2 thì \(y=\dfrac{1}{2}\cdot2^2=2\)

Khi x=-1 thì \(y=\dfrac{1}{2}\cdot\left(-1\right)+1=1-\dfrac{1}{2}=\dfrac{1}{2}\)

vậy: \(A\left(2;2\right);B\left(-1;\dfrac{1}{2}\right)\)

c: Thay x=1 vào (P), ta được:

\(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)

vậy: C(1;0,5)

A(2;2); B(-1;0,5); C(1;0,5)

\(AB=\sqrt{\left(-1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{3\sqrt{5}}{2}\)

\(AC=\sqrt{\left(1-2\right)^2+\left(0,5-2\right)^2}=\dfrac{\sqrt{13}}{2}\)

\(BC=\sqrt{\left(1+1\right)^2+\left(0,5-0,5\right)^2}=2\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{\dfrac{45}{4}+\dfrac{13}{4}-4}{2\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}}=\dfrac{7}{\sqrt{65}}\)

=>\(sinBAC=\sqrt{1-\left(\dfrac{7}{\sqrt{65}}\right)^2}=\dfrac{4}{\sqrt{65}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{4}{\sqrt{65}}\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{\sqrt{13}}{2}=\dfrac{3}{2}\)