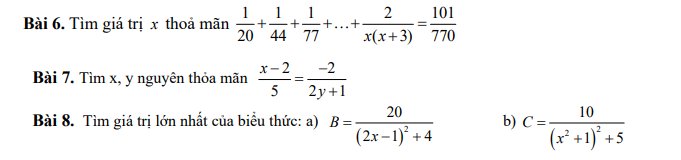
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: KHi xét nghiệm viêm gan thì có 2 kết quả có thể xảy ra: Dương tính, Âm tính
b: Xác suất thực nghiệm là:
\(\dfrac{26}{230}=\dfrac{13}{115}\)

$2,5\times20,21\times5\times40\times0,2$
$=(2,5\times40)\times(5\times0,2)\times20,21$
$=100\times1\times20,21$
$=100\times20,21=2021$
\(2,5\cdot20,21\cdot5\cdot40\cdot0,2\\=\left(2,5\cdot40\right)\cdot20,21\cdot\left(5\cdot0,2\right)\\ =\left(2,5\cdot4\cdot10\right)\cdot20,21\cdot1\\ =100\cdot20,21\\ =2021\)

\(1-\left(4\dfrac{2}{5}+x-7\dfrac{2}{3}\right):15\dfrac{1}{3}=0\\ 1-\left(\dfrac{22}{5}+x-\dfrac{23}{3}\right):\dfrac{46}{3}=0\\ 1-\left(\dfrac{-49}{15}+x\right):\dfrac{46}{3}=0\\ \left(\dfrac{-49}{15}+x\right):\dfrac{46}{3}=1\\ -\dfrac{49}{15}+x=\dfrac{46}{3}\\ x=\dfrac{46}{3}+\dfrac{49}{15}\\ x=\dfrac{279}{15}=\dfrac{93}{5}\)
$1-\left(4.\frac25+x-\frac{7.2}{3}\right):15.\frac13=0$
$\Rightarrow \left(\frac85-\frac{14}{3}+x\right):15:3=1$
$\Rightarrow \left(-\frac{46}{15}+x\right):15=3$
$\Rightarrow -\frac{46}{15}+x=3.15$
$\Rightarrow -\frac{46}{15}+x=45$
$\Rightarrow x=45-\left(-\frac{46}{15}\right)=\frac{721}{15}$

\(56=2^3\cdot7;140=2^2\cdot5\cdot7\)
=>\(ƯCLN\left(56;140\right)=2^2\cdot7=28\)
Ta có:
\(56=7\cdot8=7\cdot2^3\)
\(140=4\cdot35=2^2\cdot5\cdot7\)
\(=>ƯCLN\left(56;140\right)=7\cdot2^2=28\)

\(x+x:2+x:3=11\)
=>\(x+\dfrac{1}{2}x+\dfrac{1}{3}x=11\)
=>\(x\left(\dfrac{1}{2}+\dfrac{1}{3}+1\right)=11\)
=>\(x\cdot\dfrac{11}{6}=11\)
=>\(x=11:\dfrac{11}{6}=6\)

\(S=\dfrac{1}{18}+\dfrac{1}{18\cdot9}+\dfrac{1}{162\cdot9}+\dfrac{1}{1452\cdot9}\)
\(=\dfrac{1}{9}\left(\dfrac{1}{2}+\dfrac{1}{18}+\dfrac{1}{162}+\dfrac{1}{1452}\right)\)
\(=\dfrac{1}{9}\cdot\left(\dfrac{81}{162}+\dfrac{9}{162}+\dfrac{1}{162}+\dfrac{1}{1452}\right)\)
\(=\dfrac{1}{9}\cdot\left(\dfrac{91}{162}+\dfrac{1}{1452}\right)=\dfrac{1}{9}\cdot\left(\dfrac{22022}{39204}+\dfrac{27}{39204}\right)\)
\(=\dfrac{1}{9}\cdot\dfrac{22049}{39204}=\dfrac{22049}{352836}\)
\(S=\dfrac{1}{18}+\dfrac{1}{18\cdot9}+\dfrac{1}{162\cdot9}+\dfrac{1}{1452\cdot9}\\ =\dfrac{1}{9\cdot2}+\dfrac{1}{9^2\cdot2}+\dfrac{1}{9^3\cdot2}+\dfrac{1}{9^4\cdot2}\\ =\dfrac{1}{2}\left(\dfrac{1}{9}+\dfrac{1}{9^2}+\dfrac{1}{9^3}+\dfrac{1}{9^4}\right)\)
Đặt:
\(K=\dfrac{1}{9}+\dfrac{1}{9^2}+\dfrac{1}{9^3}+\dfrac{1}{9^4}=>9K=1+\dfrac{1}{9}+\dfrac{1}{9^2}+\dfrac{1}{9^3}\\ =>9K-K=1+\dfrac{1}{9}+\dfrac{1}{9^2}+\dfrac{1}{9^3}-\dfrac{1}{9}-\dfrac{1}{9^2}-\dfrac{1}{9^3}-\dfrac{1}{9^4}\\ =>8K=1-\dfrac{1}{9^4}=\dfrac{9^4-1}{9^4}\\ =>K=\dfrac{9^4-1}{8\cdot9^4}\)
\(=>S=\dfrac{1}{2}\cdot\dfrac{9^4-1}{8\cdot9^4}=\dfrac{9^4-1}{16\cdot9^4}\)

a: \(12-\left(-0,6\right)=12+0,6=12,6\)
b: \(\left(-0,25\right)\cdot1,24=-\dfrac{1}{4}\cdot\dfrac{31}{25}=\dfrac{-31}{100}\)
c: \(\left(-4,5\right)+\left(17,45\right)=17,45-4,5=12,95\)
d: \(\dfrac{-5,85}{2,25}=\dfrac{-585}{225}=-\dfrac{13}{5}=-2,6\)

\(2,5=\dfrac{5}{2}\)
Hiệu số phần bằng nhau là: 5-2=3(phần)
Số quả trứng của bà thứ nhất là:
24:3x5=40(quả)
Số quả trứng của bà thứ hai là:
40-24=16(quả)
Hiệu số phần bằng nhau là: 5-2=3(phần)
Số quả trứng của bà thứ nhất là:
24:3x5=40(quả)
Số quả trứng của bà thứ hai là:
40-24=16(quả)
Bài 7:
\(\dfrac{x-2}{5}=\dfrac{-2}{2y+1}\)
=>\(\left(x-2\right)\left(2y+1\right)=5\cdot\left(-2\right)=-10\)
mà 2y+1 lẻ
nên \(\left(x-2;2y+1\right)\in\left\{\left(10;-1\right);\left(-10;1\right);\left(2;-5\right);\left(-2;5\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(12;-1\right);\left(-8;0\right);\left(4;-3\right);\left(0;2\right)\right\}\)
Bài 6:
\(\dfrac{1}{20}+\dfrac{1}{44}+\dfrac{1}{70}+...+\dfrac{2}{x\left(x+3\right)}=\dfrac{101}{770}\)
=>\(\dfrac{2}{40}+\dfrac{2}{88}+\dfrac{2}{140}+...+\dfrac{2}{x\left(x+3\right)}=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+...+\dfrac{3}{x\left(x+3\right)}\right)=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{x}-\dfrac{1}{x+3}\right)=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{1}{5}-\dfrac{1}{x+3}\right)=\dfrac{101}{770}\)
=>\(\dfrac{1}{5}-\dfrac{1}{x+3}=\dfrac{101}{770}:\dfrac{2}{3}=\dfrac{101}{770}\cdot\dfrac{3}{2}=\dfrac{303}{1540}\)
=>\(\dfrac{1}{x+3}=\dfrac{1}{5}-\dfrac{303}{1540}=\dfrac{1}{308}\)
=>x+3=308
=>x=305
Bài 8:
a: \(\left(2x-1\right)^2+4>=4\forall x\)
=>\(B=\dfrac{20}{\left(2x-1\right)^2+4}< =\dfrac{20}{4}=5\forall x\)
Dấu '=' xảy ra khi 2x-1=0
=>\(x=\dfrac{1}{2}\)
b: \(x^2+1>=1\forall x\)
=>\(\left(x^2+1\right)^2>=1^2=1\forall x\)
=>\(\left(x^2+1\right)^2+5>=1+5=6\forall x\)
=>\(C=\dfrac{10}{\left(x^2+1\right)^2+5}< =\dfrac{10}{6}=\dfrac{5}{3}\forall x\)
Dấu '=' xảy ra khi x=0