phương trình ( m^2 -m )x +1=m^2 (ẩn x) vô số nghiệm khi và chỉ khi:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔCMN vuông tại M và ΔCAB vuông tại A có
\(\widehat{MCN}\) chung
Do đó: ΔCMN~ΔCAB
c: Ta có: \(\widehat{BAN}+\widehat{CAN}=\widehat{BAC}=90^0\)
\(\widehat{BNA}+\widehat{NAH}=90^0\)(ΔAHN vuông tại H)
mà \(\widehat{BAN}=\widehat{BNA}\)(ΔBAN cân tại B)
nên \(\widehat{CAN}=\widehat{NAH}\)
=>AN làphân giác của góc HAC

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔCMN vuông tại M và ΔCAB vuông tại A có
\(\widehat{MCN}\) chung
Do đó: ΔCMN~ΔCAB
c: Ta có: \(\widehat{CAN}+\widehat{BAN}=\widehat{CAB}=90^0\)
\(\widehat{HAN}+\widehat{BNA}=90^0\)(ΔNHA vuông tại H)
mà \(\widehat{BAN}=\widehat{BNA}\)(ΔBAN cân tại B)
nên \(\widehat{CAN}=\widehat{HAN}\)
=>AN là phân giác của góc HAC

Câu 16:
13h15p-13h=15p=0,25 giờ
Gọi thời gian từ lúc Ngọc đến nhà Hà cho đến lúc hai bạn gặp nhau là x(giờ)
(Điều kiện: x>0)
Sau x+0,25 giờ, Hà đi được:
10(x+0,25)(km)
Sau x giờ, Ngọc đi được: 16x(km)
Do đó, ta có phương trình:
16x=10(x+0,25)
=>6x=2,5
=>x=2,5/6=5/12(nhận)
Vậy: Hai bạn gặp nhau sau khi Ngọc đi được 5/12 giờ=25 phút
=>Hai bạn gặp nhau lúc 13h15p+25p=13h40p
Gọi khoảng thời gian mà Ngọc cần đi để đuổi kịp Hà là x (giờ) với x>0
Hà đi trước Ngọc một khoảng: 13 giờ 15 phút -13 giờ =15 phút =0,25 giờ
Thời gian Hà đi đến khi bị Ngọc đuổi kịp: \(x+0,25\) giờ
Quãng đường Hà đã đi được đến khi bị Ngọc đuỏi kịp: \(10\left(x+0,25\right)\) (km)
Quãng đường Ngọc đi đến khi đuổi kịp Hà: \(16x\) (km)
Do 2 người gặp nhau nên quãng đường đi bằng nhau, ta có pt:
\(10\left(x+0,25\right)=16x\)
\(\Leftrightarrow6x=2,5\)
\(\Leftrightarrow x=\dfrac{5}{12}\) (giờ) = 25 phút
Vậy Ngọc đuổi kịp Hà lúc 13 giờ 15 phút + 25 phút =13 giờ 40 phút

A B M C D K E F
a/
Xét \(\Delta AMD\) và \(\Delta BMC\) có
MD = MB (cạnh tg đều BMD) (1)
MA = MC (cạnh tg đều AMC) (2)
\(\widehat{AMD}=\widehat{AMB}-\widehat{BMD}=180^o-60^o=120^o\)
\(\widehat{BMC}=\widehat{AMB}-\widehat{AMC}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{AMD}=\widehat{BMC}=120^o\) (3)
Từ (1) (2) (3) => \(\Delta AMD=\Delta BMC\left(c.g.c\right)\Rightarrow AD=BC\)
b/
Xét \(\Delta AEM\) và \(\Delta CFM\) có
MA = MC (cạnh tg đều AMC) (4)
\(AD=BC\left(cmt\right);AE=\dfrac{AD}{2};CF=\dfrac{BC}{2}\Rightarrow AE=CF\) (5)
\(\Delta AMD=\Delta BMC\left(cmt\right)\Rightarrow\widehat{MAD}=\widehat{MCB}\) (6)
Từ (4) (5) (6) \(\Rightarrow\Delta AEM=\Delta CFM\left(c.g.c\right)\)
\(\Rightarrow ME=MF\) và \(\widehat{AME}=\widehat{CMF}\)
Ta có
\(\widehat{AME}+\widehat{EMC}=\widehat{AMC}=60^o\)
\(\Rightarrow\widehat{CMF}+\widehat{EMC}=\widehat{EMF}=60^o\)
=> \(\Delta MEF\) là tg đều

Gọi vận tốc riêng của cano là x(km/h)
(Điều kiện: x>4)
Vận tốc lúc đi là x+4(km/h)
Vận tốc lúc về là x-4(km/h)
2h30p=2,5(giờ)
Độ dài quãng đường lúc đi là 2(x+4)(km)
Độ dài quãng đường lúc về là 2,5(x-4)(km)
Do đó, ta có phương trình:
2,5(x-4)=2(x+4)
=>2,5x-10=2x+8
=>0,5x=18
=>x=36(nhận)
Vậy: vận tốc riêng của cano là 36km/h
Gọi x (km/h) là vận tốc riêng của ca nô (x > 4)
Vận tốc khi đi xuôi dòng: x + 4 (km/h)
Vận tốc khi đi ngược dòng: x - 4 (km/h)
2 giờ 30 phút = 2,5 h
Quãng đường đi từ A đến B: 2(x + 4) (km)
Quãng đường đi từ B về A: 2,5(x - 4) (km)
Theo đề bài, ta có phương trình:
2(x + 4) = 2,5(x - 4)
2x + 8 = 2,5x - 10
2,5x - 2x = 8 + 10
0,5x = 18
x = 18 : 0,5
x = 36 (nhận)
Vậy vận tốc riêng của ca nô là 36 km/h

\(x+y+z=xyz\Rightarrow\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{zx}=1\)
\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\sqrt{3}\Rightarrow\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2=3\)
\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}=3\)
\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+2.1=3\)
\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=1\)

a: Xét ΔAHB vuông tại H và ΔABC vuông tại B có
\(\widehat{HAB}\) chung
Do đó: ΔAHB~ΔABC
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{ACB}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HA^2=HB\cdot HC\)
c: ta có: BH\(\perp\)AC
AD\(\perp\)AC
Do đó: BH//AD
Xét ΔCDO có BI//DO
nên \(\dfrac{BI}{DO}=\dfrac{CI}{CO}\left(1\right)\)
Xét ΔCOA có IH//OA
nên \(\dfrac{IH}{OA}=\dfrac{CI}{CO}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{BI}{DO}=\dfrac{IH}{OA}\)
mà DO=OA
nên BI=IH
=>I là trung điểm của BH

a: Xét ΔABC có AD là phân giác
nên \(\dfrac{CD}{AC}=\dfrac{BD}{AB}\)
=>\(\dfrac{CD}{5}=\dfrac{2}{3}\)
=>\(CD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
\(BC=BD+CD=\dfrac{10}{3}+2=\dfrac{16}{3}\left(cm\right)\)
b: Xét ΔBAD có BI là phân giác
nên \(\dfrac{AI}{ID}=\dfrac{BA}{BD}\)
=>\(\dfrac{AI}{ID}=\dfrac{CA}{CD}\)
=>\(AI\cdot CD=CA\cdot ID\)



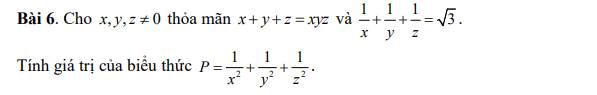


\(\left(m^2-m\right)x+1=m^2\)
=>\(\left(m^2-m\right)x=m^2-1\)
Để phương trình có vô số nghiệm thì \(\left\{{}\begin{matrix}m^2-m=0\\m^2-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\\left(m-1\right)\left(m+1\right)=0\end{matrix}\right.\)
=>m=1
\(\Leftrightarrow\left(m^2-m\right)x=m^2-1\)
Pt có vô số nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-m=0\\m^2-1=0\end{matrix}\right.\) \(\Rightarrow m=1\)