Do `\Delta ABC` đều 

`-> AB=AC=BC`

`-> AB = 2BH`

Xét `\Delta ABH` vuông tại `H` `( AH` là đường cao `)`

ta có `:` `AB^2 = BH^2 + AH^2`

`=> 4BH^2 = BH^2 + AH^2`

`=> 3BH^2 = AH^2`

`=> BH = ( AH )/( \sqrt{3} )`

`=> a = AB = ( AH )/( \sqrt{3} )`

Vậy `...` 

`=> a = AB = ( AH )/( \sqrt{3} )`

dòng cuối 

giúp mình với ạ

Ta có: \(\left|3x+4\right|+\left|3x-1\right|=\left|3x+4\right|+\left|1-3x\right|\)

Theo bất đẳng thức: \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\), ta có:

\(\left|3x+4\right|+\left|1-3x\right|\ge\left|3x+4+1-3x\right|=5\Rightarrow\left|3x+4\right|+\left|3x-1\right|\ge5\) (*)

Mặt khác:

Với mọi x ta có:

\(3\left(x+1\right)^2\ge0\Rightarrow3\left(x+1\right)^2+4\ge4\Rightarrow\dfrac{20}{3\left(x+1\right)^2+4}\le\dfrac{20}{4}\Rightarrow\dfrac{20}{3\left(x+1\right)^2+4}\le5\) (**)

Từ (*)(**) \(\Rightarrow\dfrac{20}{3\left(x+1\right)^2+4}=5\)

\(\Rightarrow3\left(x+1\right)^2+4=4\)

\(\Rightarrow3\left(x+1\right)^2=0\)

\(\Rightarrow\left(x+1\right)^2=0\)

\(\Rightarrow x=-1\)

Xét: 2x² + 5x = 0

2.x.x + 5x = 0

x ( 2x + 5 ) = 0

x = 0 hoặc 2x + 5 = 0

                  2x       = -5

                  2x = \(-\dfrac{5}{2}\)

Vậy x = 0 ; x = \(-\dfrac{5}{2}\)

`( 5^5 )/( 5^x ) = 5^{18}`

`<=> 5^{5-x} = 5^{18}`

`=> 5-x=18`

`<=> x=5-18`

`<=> x=-13`

Vậy `x=-13`

?

\(a)\dfrac{5x+4}{x^2+1}=0\)

\(\Rightarrow5x+4=0\)

\(\Rightarrow x=-\dfrac{4}{5}\)

Vậy \(A=0\Leftrightarrow x=-\dfrac{4}{5}\)

\(b)\dfrac{5x+4}{x^2+1}>0\)

Do \(x^2+1>0\forall x\)

\(\Rightarrow5x+3>0\)

\(\Rightarrow x>-\dfrac{4}{5}\)

Vậy \(A>0\Leftrightarrow x>-\dfrac{4}{5}\)

\(c)\dfrac{5x+4}{x^2+1}< 0\)

Do \(x^2+1>0\forall x\)

\(\Rightarrow5x+4< 0\)

\(\Rightarrow x< -\dfrac{4}{5}\)

Vậy \(A< 0\Leftrightarrow x< -\dfrac{4}{5}\)

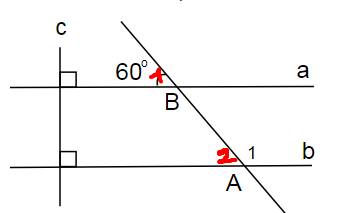
Vì a \(\perp\) c và b \(\perp\) c nên a//b

=>\(\hat{B_1}=\hat{A_2}\)=60⁰ (hai góc đồng vị)

Mà \(\hat{A_2}\) và \(\hat{A_1}\)là hai góc kề bù

=> \(\hat{A_1}+\hat{A_2}=180^o\)

hay \(\hat{A_1}\) + 60^o=180^o

=> \(\hat{A_1}\) = 180^o-60^o=120^o

Vậy \(\hat{A_1}\)=120⁰

5