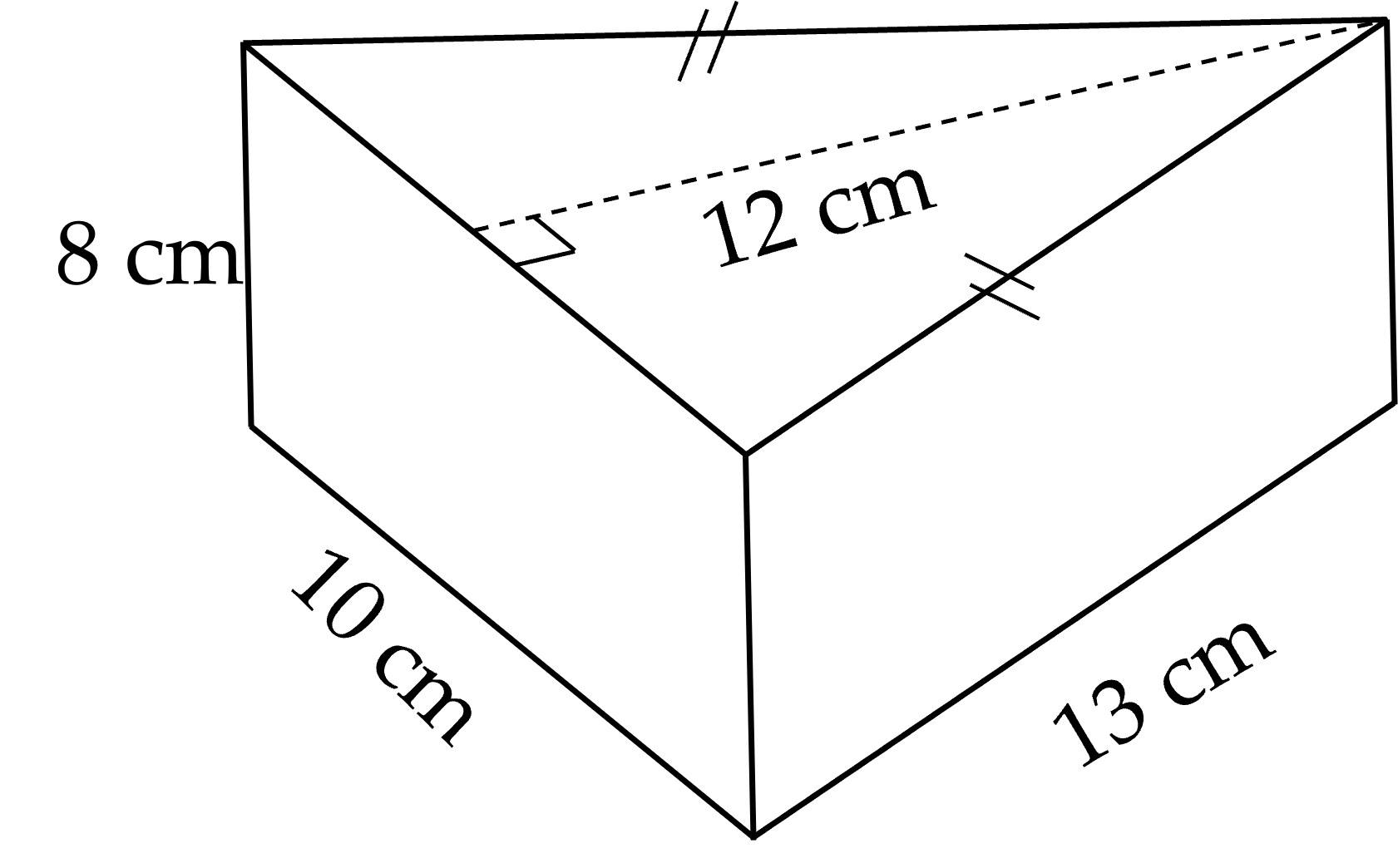
bài 3 : cho lăng trụ đứng ABC . A'B'C' có đáy tam giác ABC vuông tại A , AB=15cm , BC=25cm , A'=12 cm , thể tích của hình lăng trụ đứng ABC.A'B'C' là 1800cm3 . tính diện tích xung quanh của hình lăng trụ đứng ABC.A'B'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, olm cảm ơn em đã lựa chọn đồng hành cùng olm, cảm ơn những đánh giá của em về chất lượng bài giảng của olm.
Olm chúc học tập vui vẻ và hiệu quả cùng olm em nhé.

a, \(\Delta\)ABC = \(\Delta\) DMN
⇒ \(\widehat{B}\) = \(\widehat{M}\) = 600
b; \(\Delta\)ABC = \(\Delta\) DMN
⇒ BC = MN = 6 cm
AC = DN = 4 cm

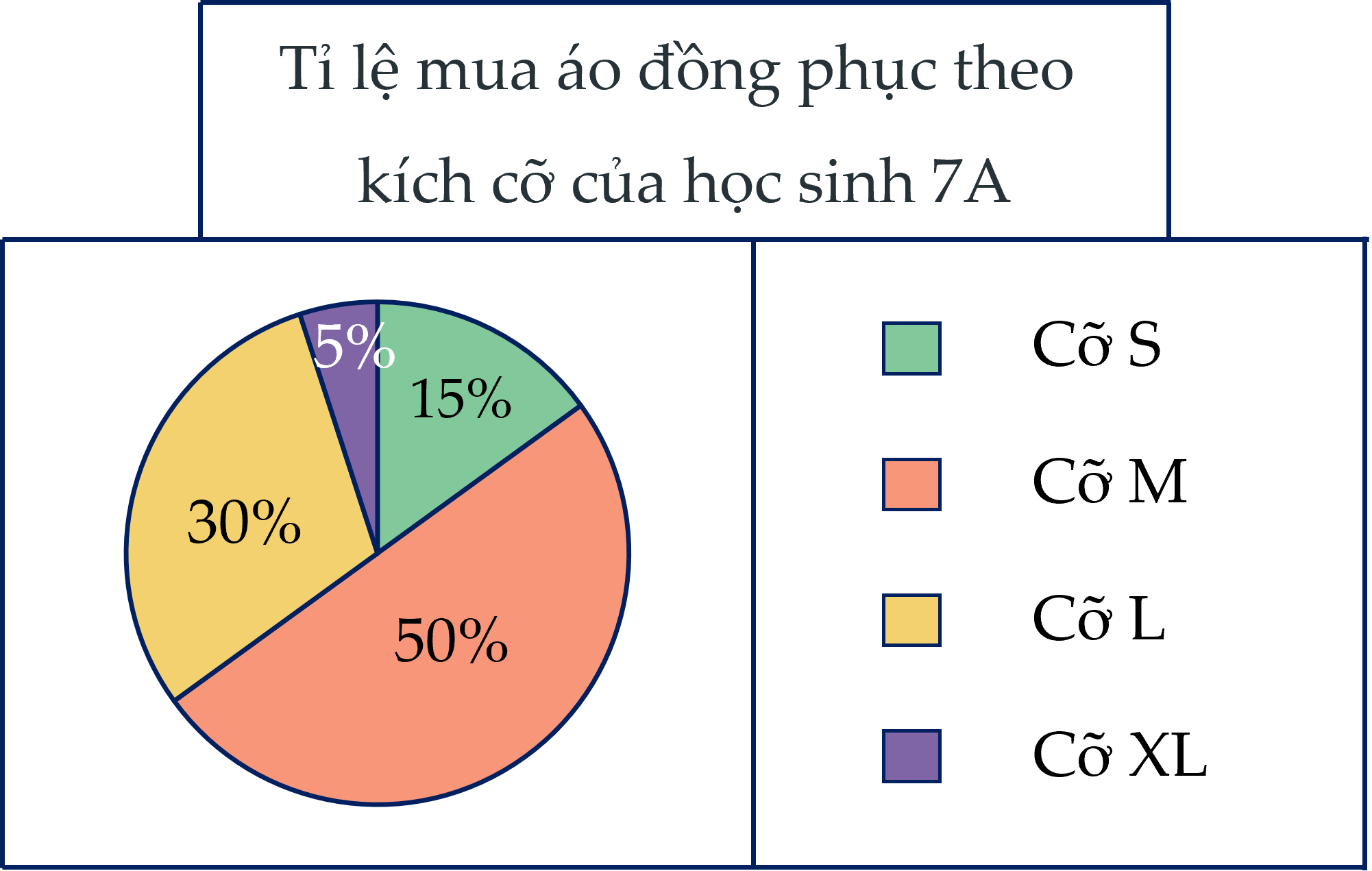
a) Cỡ áo nào có tỉ lệ học sinh đặt mua nhiều nhất? -> Cỡ M
b) Cỡ áo nào có tỉ lệ học sinh đặt mua ít nhất? -> Cỡ XL
c) Biết lớp 7A có 40 học sinh. Tính số lượng bạn đã mua áo đồng phục mỗi loại.
Số bạn mua áo cỡ S:
\(15\%.40=6\left(HS\right)\)
Số bạn mua áo cỡ M:
\(50\%.40=20\left(HS\right)\)
Số bạn mua áo cỡ L:
\(30\%.40=12\left(HS\right)\)
Số bạn mua áo cỡ XL:
\(5\%.40=2\left(HS\right)\)
Đ.số:.......

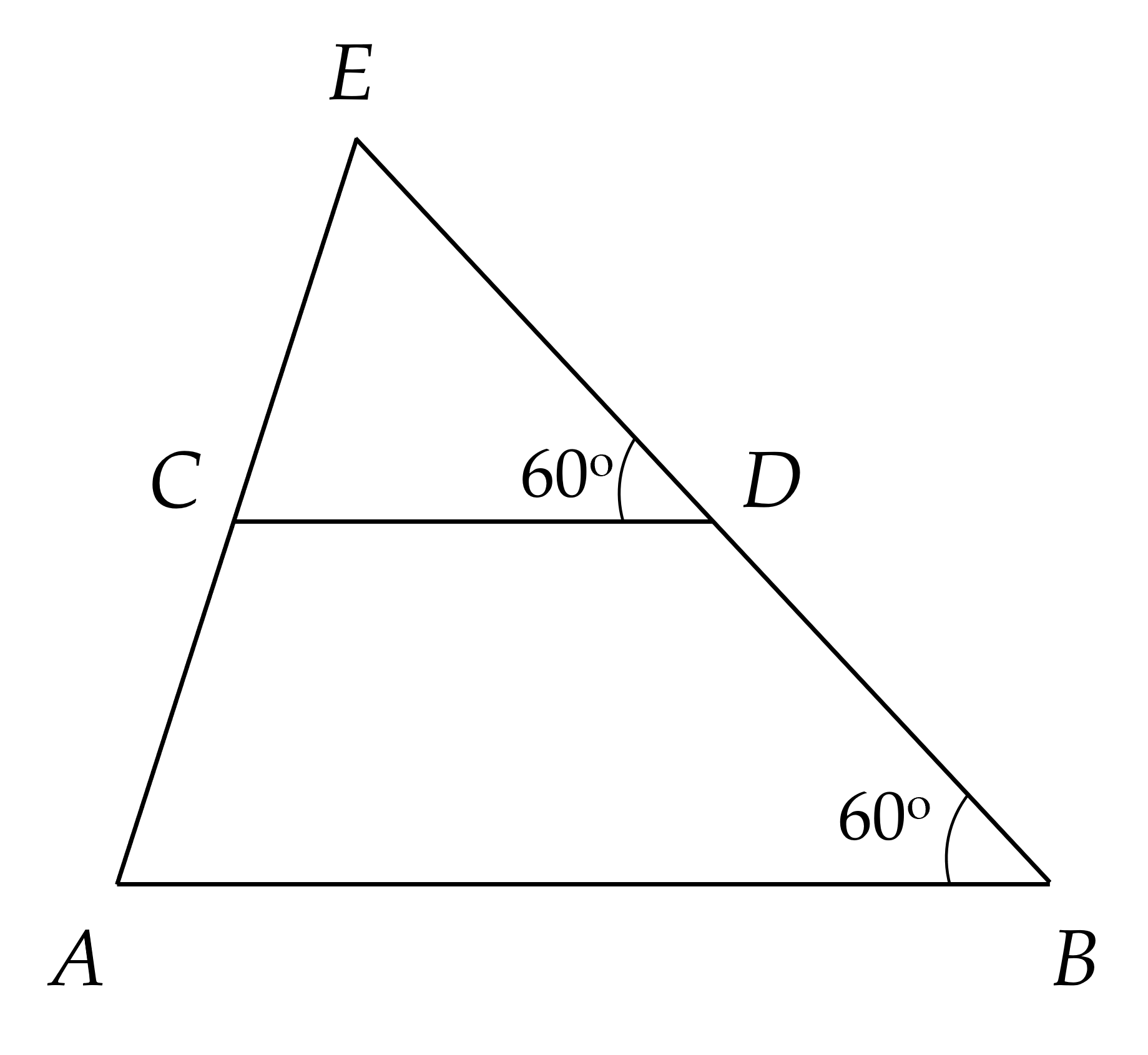
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
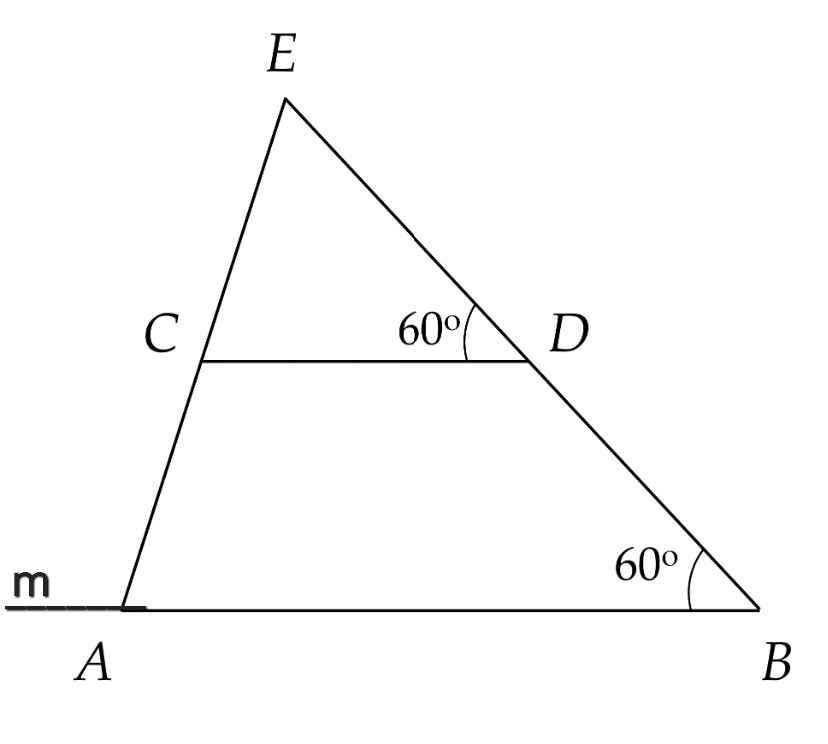
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

2/3 - |x - 1/2| = 2/3
|x - 1/2| = 2/3 - 2/3
|x - 1/2| = 0
x - 1/2 = 0
x = 0 + 1/2
x = 1/2

11/3 . 2/5 + 11/3 . 8/5 - 11/3
= 11/3 . (2/5 + 8/5 - 1)
= 11/3 . (2 - 1)
= 11/3 . 1
= 11/3

Thể tích của một viên gạch là: 2 x 1 x 0,5 = 1 (dm3)
Thể tích của 25 viên gạch là: 1 x 25 = 25 (dm3)
Khi thả 25 viện gạch vào thùng thì mực nước tăng thêm là:
25 : 7 : 7 = \(\dfrac{25}{49}\) (dm)
Lấy 25 chia 7 chia 7 vì muốn tính chiều cao của mực nước tăng thêm ta phải lấy thể tích chia cho diện tích đáy em nhé)
Khi ta thả thêm 25 viên gạch thì mực nước cách miệng bể là:
7 - (4 + \(\dfrac{25}{49}\)) = \(\dfrac{122}{49}\) (dm)
Đáp số: .....

Thanh chì 10cm3 nặng:
108: (19-10) x 10 = 120(gam)
Thanh chì 19cm3 nặng:
120 + 108 = 228(gam)
Đ.số:......