|
< |
|
< |
|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu vi mặt đáy của hình hộp chữ nhật là:
\(\left(10+6\right)\times2=32\left(dm\right)\)
Chiều cao của hình hộp chữ nhật là:
\(144\div32=4,5\left(dm\right)\)
Đáp số: \(4,5dm\)
Tổng chiều dài và rộng của hình hợp chữ nhật:
\(6+10=16\left(dm\right)\)
Chiều cao của hình hộp chữ nhật là:
\(144:2:16=4,5\left(dm\right)\)
Đáp số: ...

`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
`x + 12 = 25`
`\Rightarrow x = 25 - 12`
`\Rightarrow x = 13`
Vậy, `x = 13`
`b)`
`134 - x = 125 \div 5`
`\Rightarrow 134 - x = 25`
`\Rightarrow x = 134 - 25`
`\Rightarrow x=109`
Vậy, `x = 109`
`c)`
`2 \times x - 53 = 22`
`\Rightarrow 2x = 22 + 53`
`\Rightarrow 2x = 75`
`\Rightarrow x = 75 \div 2`
`\Rightarrow x =37,5`
Vậy, `x = 37,5`
`d)`
`7 + 3 \times x = 16`
`\Rightarrow 3x = 16 - 7`
`\Rightarrow 3x =9`
`\Rightarrow x = 9 \div 3`
`\Rightarrow x = 2`
Vậy, `x = 2.`
`2,`
`a)`
`(x + 3) - 15 = 2`
`\Rightarrow x + 3 = 2 + 15`
`\Rightarrow x +3 = 17`
`\Rightarrow x = 17 - 3`
`\Rightarrow x = 14`
Vậy, `x = 14`
`b)`
`33 + (x - 1) = 56`
`\Rightarrow x - 1 = 56 - 33`
`\Rightarrow x - 1 = 23`
`\Rightarrow x = 23 + 1`
`\Rightarrow x = 24`
Vậy, `x = 24`
`c)`
`5 \times (4 + 6 \times x) = 290`
`\Rightarrow 4 + 6x = 290 \div 5`
`\Rightarrow 4 + 6x = 58`
`\Rightarrow 6x = 58 - 4`
`\Rightarrow 6x = 54`
`\Rightarrow x = 54 \div 6`
`\Rightarrow x = 9`
Vậy, `x = 9`
`d)`
`x. 3,7 + x. 6,3 = 120`
`\Rightarrow x . (3,7 + 6,3) = 120`
`\Rightarrow x . 10 = 120`
`\Rightarrow x = 120 \div 10`
`\Rightarrow x = 12`
Vậy,` x = 12.`
$#KDN040510$

bài 1 :
a) Ta có MQ//NP (theo giả thiết).
Chứng minh MN = PQ:
Vì MN//PQ và MQ//NP, ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
b) Ta có MN = PQ (theo giả thiết).
Chứng minh MQ//NP:
Giả sử MQ không // NP. Khi đó, MQ và NP sẽ cắt nhau tại một điểm O.
Vì MN//PQ và MQ//NP, nên ta có hai tam giác MNP và QMQ' đồng dạng (theo nguyên lý đồng dạng của tam giác có hai cặp góc tương đồng bằng nhau).
Do đó, ta có tỉ số đồng dạng giữa các cạnh của hai tam giác là:
MN/MQ = NP/QM
Từ đó suy ra: MN/MQ = NP/NP
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MN/MQ = NP/NP
Từ đó suy ra: MN = PQ.
Điều này mâu thuẫn với giả thiết MN = PQ (đã cho). Vậy giả sử MQ không // NP là sai.
Do đó, ta kết luận rằng MQ//NP.
Chứng minh MQ = NP:
Vì MQ//NP, nên ta có tỉ số đồng dạng:
MQ/MN = NP/PQ
Vì MN = PQ (đã chứng minh ở trên), nên ta có tỉ số đồng dạng:
MQ/MN = NP/NP
Từ đó suy ra: MQ = NP.
bài 2 :
a) Ta có MN = MQ và góc M = 50 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc N = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
50 độ + góc N + 90 độ + góc N = 360 độ
Simplifying the equation:
140 độ + 2góc N = 360 độ
Trừ 140 độ từ hai phía:
2góc N = 220 độ
Chia cho 2:
góc N = 110 độ
Vậy số đo góc MQN là 110 độ.
b) Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + 110 độ + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + 200 độ = 360 độ
Trừ 200 độ từ hai phía:
2góc M = 160 độ
Chia cho 2:
góc M = 80 độ
Vậy số đo góc MQP là 80 độ.
c) Để chứng minh MP vuông góc với NQ, ta cần chứng minh rằng góc MPN + góc NQP = 90 độ.
Ta đã biết góc P = 90 độ. Vì tứ giác MNPQ là tứ giác cân (hai cạnh bằng nhau), nên góc M = góc Q.
Vì tổng các góc trong một tứ giác bằng 360 độ, ta có:
góc M + góc N + góc P + góc Q = 360 độ
Thay giá trị vào, ta có:
góc M + góc N + 90 độ + góc M = 360 độ
Simplifying the equation:
2góc M + góc N = 270 độ
Vì góc M = góc Q, nên ta có:
2góc M + góc M = 270 độ

với 4 chữ số 2 và các phép tính , hãy lặp các dãy tính có kết quả lần lượt là 0,1,2,3,4,5,6,7,8,9,10

0=2-2+2-2
1=2:2+2-2
2=2:2+2:2
3=2x2-2:1
4=2x2x2:2
5=2:2+2x2
6=2x2x2-2
7=
8=2x2+2x2
9=
10=2x2x2+2
7 và 9 khó quá nhớ tick cho mik nhé


Đặt : A = 1111...111 (2022 chữ số 1)
Tổng các chữ số của số A là:
1 \(\times\) 2022 = 2022
xét số 2022 ta có: tổng các chữ số của số 2022 là:
2 + 0 + 2 + 2 = 6
6 : 9 = 0 dư 6
⇒ A chia 9 dư 6 Vậy để A ⋮ 9 thì phải thêm vào A số đơn vị là:
9 - 6 = 3 (đơn vị)
Kết luận để một số được viết bằng 2022 chữ số 1 chia hết cho 9 thì cần cộng thêm vào số đó 3 đơn vị
một số được viết từ 2022 chữ số 1=> Số đó có tổng các chữ số là 2022.Vậy phải cộng thêm ít nhất 3 đơn vị để số đó ⋮9.

Tuổi con là:
85:(36+40+9)x9=9(tuổi)
Tuổi mẹ là:
85:(36+40+9)x36=36(tuổi)
Vậy tuổi bố là:
85-(36+9)=40(tuổi)
Bài giải
Con bằng \(\dfrac{1}{4}\) tuổi mẹ, mẹ bằng \(\dfrac{9}{10}\) tuổi bố. Vậy có nghĩa là con bằng \(\dfrac{9}{36}\) tuổi mẹ, mẹ bằng \(\dfrac{36}{40}\)
Coi tuổi con là \(9\) phần bằng nhau, tuổi mẹ là \(36\) phần bằng nhau và tuổi bố là \(40\) phần như thế.
Tổng số phần bằng nhau là:
\(9+36+40=85\)(phần)
Tuổi con là:
\(85:85\times9=9\)(tuổi)
Tuổi mẹ là:
\(85:85\times36=36\)(tuổi)
Tuổi bố là:
\(85-9-36=40\)(tuổi)
Đ/s: Con: \(9\) tuổi; Mẹ: \(36\) tuổi; Bố: \(40\) tuổi

Câu 4:
a; 320 ⋮ a và 480 \(⋮\) a ⇒ a \(\in\) ƯC(320; 480)
Vì a là lớn nhất nên a \(\in\) ƯCLN(320 ;480)
320 = 26.5
480 = 25.3.5
ƯCLN { 480; 320} = 25.5 = 160 ⇒ a = 160
Kết luận a = 160
b; 360 \(⋮\) a và 600 \(⋮\) a ⇒ a \(\in\) ƯC(360 ;600)
vì a là lớn nhất nên a \(\in\) ƯCLN(360; 600)
360 = 23.32.5
600 = 23.3.52
ƯCLN(360; 600) = 23.3. 5 = 40 ⇒ a = 120
Kết luận a = 120
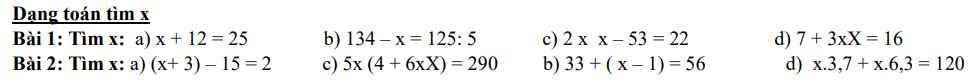
Ta có:
\(\dfrac{13}{18}=\dfrac{13\times21}{18\times21}=\dfrac{273}{378}\)
\(\dfrac{13}{17}=\dfrac{13\times21}{17\times21}=\dfrac{273}{357}\)
\(\dfrac{21}{x}=\dfrac{21\times13}{x\times13}=\dfrac{273}{13x}\)
Ta được:
\(357<13x<378\)
\(357:13<x<378:13\)
\(27,46<x<29\) (làm tròn)
Mà \(27,46<28<29\)
Vậy số thích hợp là \(28\)