Tính giá trị biểu thức: B=(3^4+4)(7^4+4)...(19^4+4)/(5^4+4)(9^4+4)...(21^4+4)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số thợ của nhóm thứ nhất, nhóm thứ hai, nhóm thứ ba lần lượt là a(người),b(người),c(người)
(Điều kiện: \(a,b,c\in Z^+\))
Nhóm thứ nhất xây xong trong 40 ngày, nhóm thứ hai xây xong trong 60 ngày, nhóm thứ ba xây xong trong 50 ngày nên ta có: 40a=60b=50c
=>4a=6b=5c
=>\(\dfrac{4a}{60}=\dfrac{6b}{60}=\dfrac{5c}{60}\)
=>\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{12}\)
Nhóm thứ ba có ít hơn nhóm thứ nhất là 3 người nên a-c=3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{12}=\dfrac{a-c}{15-12}=\dfrac{3}{3}=1\)
=>\(a=15\cdot1=15;b=10\cdot1=10;c=12\cdot1=12\)
Vậy: số thợ của nhóm thứ nhất, nhóm thứ hai, nhóm thứ ba lần lượt là 15(người),10(người),12(người)

Ta có số đó góc D, E, F của tam giác DEF tỉ lệ nghịch với 2, 3, 6 nên ta có:
\(2\widehat{D}=3\widehat{E}=6\widehat{F}\\ \Rightarrow\dfrac{2\widehat{D}}{12}=\dfrac{3\widehat{E}}{12}=\dfrac{\widehat{6F}}{12}\\ \Rightarrow\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}\)
Mà: \(\widehat{D}+\widehat{E}+\widehat{F}=180^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{\widehat{D}}{6}=\dfrac{\widehat{E}}{4}=\dfrac{\widehat{F}}{2}=\dfrac{\widehat{D}+\widehat{E}+\widehat{F}}{6+4+2}=\dfrac{180^o}{12}=15^o\)
\(\Rightarrow\widehat{D}=6\cdot15^o=90^o;\widehat{E}=15^o\cdot4=60^o;\widehat{F}=2\cdot15^o=30^o\)
Gọi số đo 3 góc D,E,F của ΔDEF lần lượt là \(d;e;f\) (o)
Điều kiện: \(d;e;f>0\)
Ta có:
+) \(d+e+f=180\) (theo định lý)
+) \(d;e;f\) tỉ lệ nghịch với 2,3,6 nên:
\(2d=3e=6f\)
\(\Rightarrow\dfrac{2d}{6}=\dfrac{3e}{6}=\dfrac{6f}{6}\)
\(\Rightarrow\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(d+e+f=180\) được:
\(\dfrac{d}{3}=\dfrac{e}{2}=\dfrac{f}{1}=\dfrac{d+e+f}{3+2+1}=\dfrac{180}{6}=30\)
Do đó:
\(\left\{{}\begin{matrix}d=3\cdot30=90\\e=2\cdot30=60\\f=1\cdot30=30\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy số đo 3 góc D,E,F của ΔDEF lần lượt là 90o;60o;30o

\(15-25\cdot8:\left(100\cdot2\right)\)
\(=15-\dfrac{200}{200}\)
=15-1
=14

2B:
a) C1: \(\dfrac{-7}{12}=\dfrac{-6-1}{12}=\dfrac{-6}{12}+\dfrac{-1}{12}=\dfrac{-1}{2}+\dfrac{-1}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{-3-4}{12}=\dfrac{-3}{12}+\dfrac{-4}{12}=\dfrac{-1}{4}+\dfrac{-1}{3}\)
C4: \(\dfrac{-7}{12}=\dfrac{-2-5}{12}=\dfrac{-2}{12}+\dfrac{-5}{12}\)
b) C1: \(\dfrac{-7}{12}=\dfrac{4-11}{12}=\dfrac{4}{12}-\dfrac{11}{12}=\dfrac{1}{3}-\dfrac{11}{12}\)
C2: \(\dfrac{-7}{12}=\dfrac{2-9}{12}=\dfrac{2}{12}-\dfrac{9}{12}=\dfrac{1}{6}-\dfrac{3}{4}\)
C3: \(\dfrac{-7}{12}=\dfrac{3-10}{12}=\dfrac{3}{12}-\dfrac{10}{12}=\dfrac{1}{4}-\dfrac{5}{6}\)

Bài 1B:
a)
\(\dfrac{-1}{16}+\dfrac{-1}{24}\\ =\dfrac{-3}{48}+\dfrac{-2}{48}\\ =\dfrac{-5}{48}\)
b)
\(\dfrac{-1}{8}-\dfrac{3}{20}\\ =\dfrac{-5}{40}-\dfrac{6}{40}\\ =\dfrac{-11}{40}\)
c)
\(-\dfrac{18}{10}+0,4\\ =\dfrac{-9}{5}+\dfrac{2}{5}\\ =\dfrac{-7}{5}\)
d)
\(6,5-\left(-\dfrac{1}{5}\right)\\ =\dfrac{13}{2}+\dfrac{1}{5}\\ =\dfrac{65}{10}+\dfrac{2}{10}\\ =\dfrac{67}{10}\)

a: ta có: \(\widehat{KAC}+\widehat{KAB}=\widehat{BAC}=90^0\)
\(\widehat{KAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
Do đó: \(\widehat{KAC}=\widehat{HBA}\)
Xét ΔKAC vuông tại K và ΔHBA vuông tại H có
AC=BA
\(\widehat{KAC}=\widehat{HBA}\)
Do đó: ΔKAC=ΔHBA
=>AK=BH
b: Ta có: ΔABC vuông cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Ta có: \(\widehat{HAM}+\widehat{HEM}=90^0\)(ΔEMA vuông tại E)
\(\widehat{HBM}+\widehat{AEB}=90^0\)(ΔEHB vuông tại H)
=>\(\widehat{HBM}=\widehat{HAM}=\widehat{KAM}\)
c: Xét ΔEHB vuông tại H và ΔEMA vuông tại M có
\(\widehat{HEB}\) chung
Do đó: ΔEHB~ΔEMA
=>\(\dfrac{EH}{EM}=\dfrac{EB}{EA}\)
=>\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
Xét ΔEHM và ΔEBA có
\(\dfrac{EH}{EB}=\dfrac{EM}{EA}\)
\(\widehat{HEM}\) chung
Do đó: ΔEHM~ΔEBA
=>\(\widehat{EHM}=\widehat{EBA}=45^0\)
Xét tứ giác AMKC có \(\widehat{AMC}=\widehat{AKC}=90^0\)
nên AMKC là tứ giác nội tiếp
=>\(\widehat{AKM}=\widehat{ACM}=45^0\)
Xét ΔMHK có \(\widehat{MHK}+\widehat{MKH}=45^0+45^0=90^0\)
nên ΔMHK vuông cân tại M

Câu 8b:
\(4\dfrac{209}{245}:\left(\dfrac{3}{5}+\dfrac{4}{7}\right)+4\dfrac{209}{245}:\left(\dfrac{2}{5}+\dfrac{3}{7}\right)\)
\(=4\dfrac{209}{245}:\dfrac{41}{35}+4\dfrac{209}{245}:\dfrac{29}{35}\)
\(=4\dfrac{209}{245}\cdot\dfrac{35}{41}+4\dfrac{209}{245}\cdot\dfrac{35}{29}\)
\(=\left(4+\dfrac{209}{245}\right)\left(\dfrac{35}{41}+\dfrac{35}{29}\right)\)
\(=\dfrac{1189}{245}\cdot35\left(\dfrac{1}{41}+\dfrac{1}{29}\right)\)
\(=\dfrac{1189}{7}\cdot\dfrac{70}{1189}=\dfrac{70}{7}=10\)

ĐKXĐ: \(x\ne-1\)
Để D là số nguyên thì \(-x+5⋮x+1\)
=>\(-x-1+6⋮x+1\)
=>\(6⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(x\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
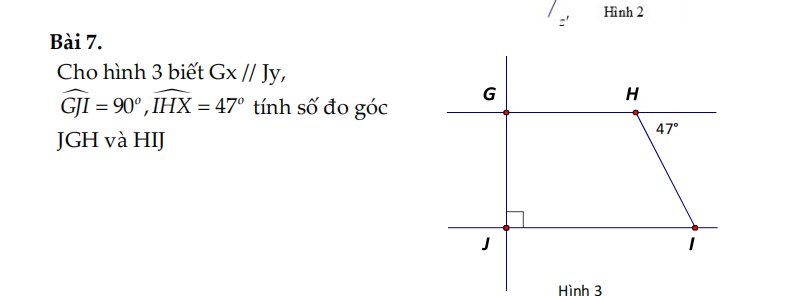 giải đầy đủ giúp em với ạ, em cảm ơn ạ.
giải đầy đủ giúp em với ạ, em cảm ơn ạ.

 giúp mình b) Câu 8 nhó
giúp mình b) Câu 8 nhó