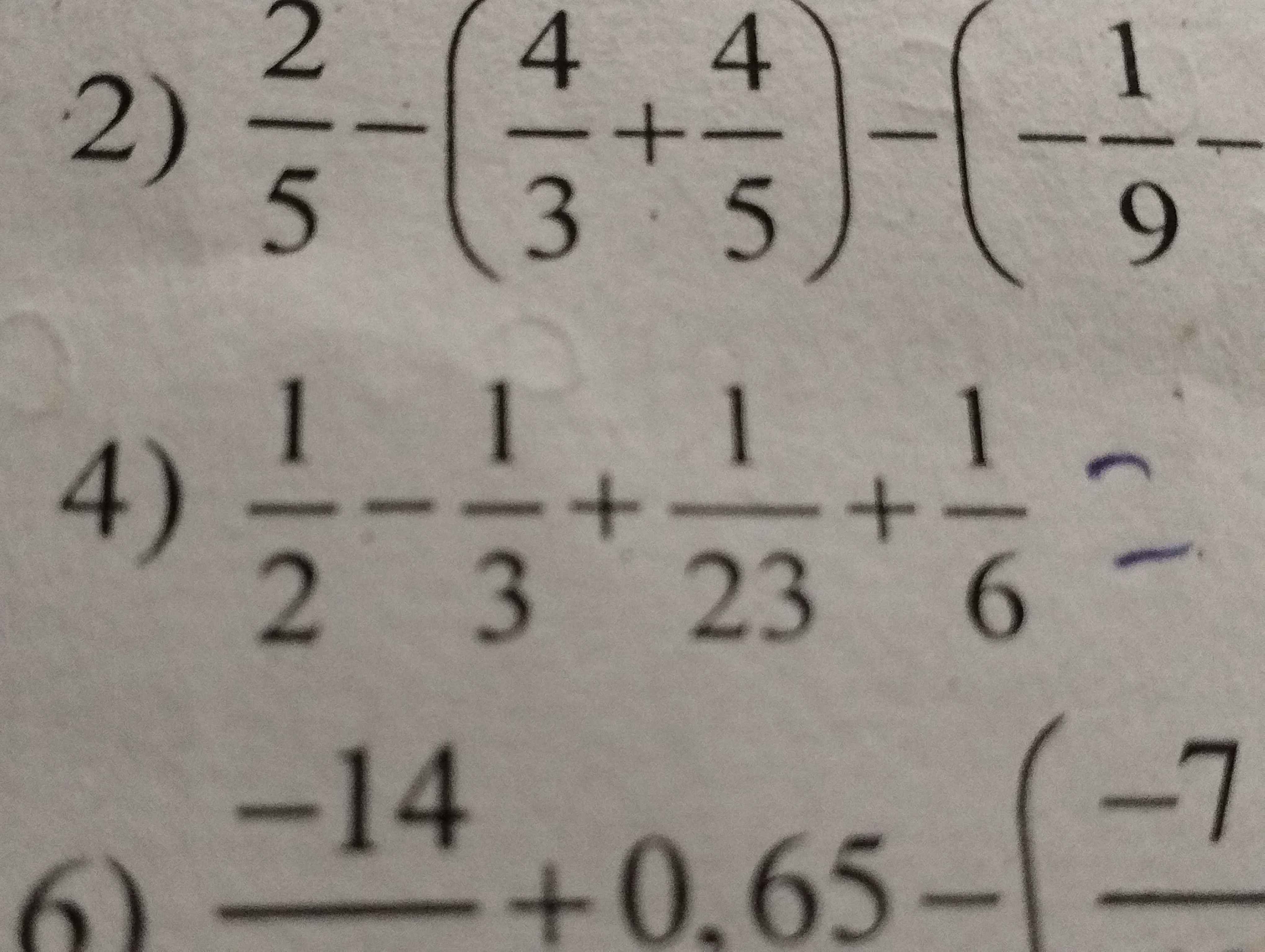 giúp mình với câu4
giúp mình với câu4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3^{x-1}+5\cdot3^{x-1}=162\\ =>3^{x-1}\cdot\left(1+5\right)=162\\ =>3^{x-1}\cdot6=162\\ =>3^{x-1}=162:6\\ =>3^{x-1}=27\\ =>3^{x-1}=3^3\\ =>x-1=3\\ =>x=1+3=4\)

\(a)A\left(x\right)=x^7-3x^2-x^5+x^4-x^2+2x-7\\ =x^7-x^5+x^4-\left(3x^2+x^2\right)+2x-7\\ =x^7-x^5+x^4-4x^2+2x-7\\ B\left(x\right)=x-2x^2+x^4-x^5-x^7-4x^2-1\\ =-x^7-x^5+x^4-\left(2x^2+4x^2\right)+x-1\\ =-x^7-x^5+x^4-6x^2+x-1\)
\(b)A\left(x\right)+B\left(x\right)\\ =\left(x^7-x^5+x^4-4x^2+2x-7\right)+\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7-x^7\right)-\left(x^5+x^5\right)+\left(x^4+x^4\right)-\left(4x^2+6x^2\right)+\left(2x+x\right)-\left(7+1\right)\\ =-x^5+2x^4-10x^2+3x-8\)
\(A\left(x\right)-B\left(x\right)=\left(x^7-x^5+x^4-4x^2+2x-7\right)-\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7+x^7\right)+\left(x^5-x^5\right)+\left(x^4-x^4\right)-\left(4x^2-6x^2\right)+\left(2x-x\right)-\left(7-1\right)\\ =2x^7+2x^2+x-6\)
c) Thay x = -1 vào C(x) = A(x) + B(x) ta có:
\(C\left(x\right)=-\left(-1\right)^5+2\cdot\left(-1\right)^4-10\cdot\left(-1\right)^2+3\cdot\left(-1\right)-8\\ =-\left(-1\right)+2\cdot1-10\cdot1-3\cdot1-8\\ =1+2-10-3-8\\ =-18\)

\(A\left(x\right)=3x^2\left(4x^3-2x+\dfrac{1}{3}\right)\\ =3x^2\cdot4x^3-3x^2\cdot2x+3x^2\cdot\dfrac{1}{3}\\ =12x^5-6x^3+x^2\\ B\left(x\right)=4x^3-\dfrac{1}{5}x\left(2x^2-x+5\right)\\ =4x^3-\dfrac{1}{5}x\cdot2x^2+\dfrac{1}{5}x\cdot x-\dfrac{1}{5}x\cdot5\\ =4x^3-\dfrac{2}{5}x^3+\dfrac{1}{5}x^2-x\\ =\dfrac{18}{5}x^3+\dfrac{1}{2}x^5-x\\ C\left(x\right)=\left(x^2-x+1\right)\left(x+1\right)-x\left(x^2+3\right)-15\\ =x^3+1-x^3-3x-15\\ =\left(x^3-x^3\right)-3x+\left(1-15\right)\\ =-3x-14\\ D\left(x\right)=-15x+5x\left(x^2-7x+3\right)-x^2\left(5x-8\right)+27x^2\\ =-15x+5x^3-35x^2+15x-5x^3+8x^2+27x^2\\ =\left(-15x+15x\right)+\left(5x^3-5x^3\right)+\left(8x^2-35x^2+27x^2\right)\\ =0\)

\(a)\left[\left(1\dfrac{2}{3}\right)^2\right]^3\\ =\left(1\dfrac{2}{3}\right)^{2\cdot3}\\ =\left(\dfrac{5}{3}\right)^6\\ b)\left(-0,18^3\right)^7\\=\left(-0,18\right)^{3\cdot7}\\ =\left(-0,18\right)^{21}\\ c)\left(\dfrac{1}{3^2}\right)^6\\ =\left[\left(\dfrac{1}{3}\right)^2\right]^6\\ =\left(\dfrac{1}{3}\right)^{2\cdot6}\\ =\left(\dfrac{1}{3}\right)^{12}\)

\(\left|x+\dfrac{1}{1\cdot3}\right|+\left|x+\dfrac{1}{3\cdot5}\right|+...+\left|x+\dfrac{1}{197\cdot199}\right|=100x\)
Số lượng số hạng là: \(\left(199-3\right):2+1=99\) (số hạng)
TH1: \(x\ge-\dfrac{1}{197\cdot199}\)
\(=>\left(x+\dfrac{1}{1\cdot3}\right)+\left(x+\dfrac{1}{3\cdot5}\right)+...+\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\\ =>99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\\ =>100x-99x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)\\ =>x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{199}\right)=\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>x=\dfrac{99}{199}\left(tm\right)\)
TH2: \(x\le-\dfrac{1}{1\cdot3}\)
\(=>-\left(x+\dfrac{1}{1\cdot3}\right)-\left(x+\dfrac{1}{3\cdot5}\right)-...-\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>-\left[\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\right]=100x\\ =>-\left[99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\right]=100\\ =>-99x-\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)=100x\\ =>100x+99x=-\dfrac{1}{2}\left(1-\dfrac{1}{199}\right)\\ =>199x=-\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>199x=-\dfrac{99}{199}\\ =>x=-\dfrac{99}{199}:199=-\dfrac{99}{39061}\left(ktm\right)\)
Vậy: `x=99/199`

Bài 3:
\(a)\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\\ \Leftrightarrow x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\\ \Leftrightarrow x^2+5x+6-x^2-3x+10=0\\ \Leftrightarrow2x+16=0\\ \Leftrightarrow2x=-16\\ \Leftrightarrow x=-\dfrac{16}{2}=-8\\ b)\left(x-3\right)\left(x-2\right)-\left(x+1\right)\left(x-5\right)=0\\ \Leftrightarrow\left(x^2-2x-3x+6\right)-\left(x^2-5x+x-5\right)=0\\ \Leftrightarrow x^2-5x+6-x^2+4x+5=0\\ \Leftrightarrow-x+11=0\\ \Leftrightarrow x=11\\ c)x\left(2x-5\right)-2x\left(x-6\right)=42\\ \Leftrightarrow2x^2-5x-2x^2+12x=42\\ \Leftrightarrow7x=42\\ \Leftrightarrow x=\dfrac{42}{7}\\ \Leftrightarrow x=6\\ d)\left(x-1\right)\left(2x+3\right)-2x\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(2x+3-2x\right)=0\\ \Leftrightarrow3\left(x-1\right)=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\)
Bài 2:
b: 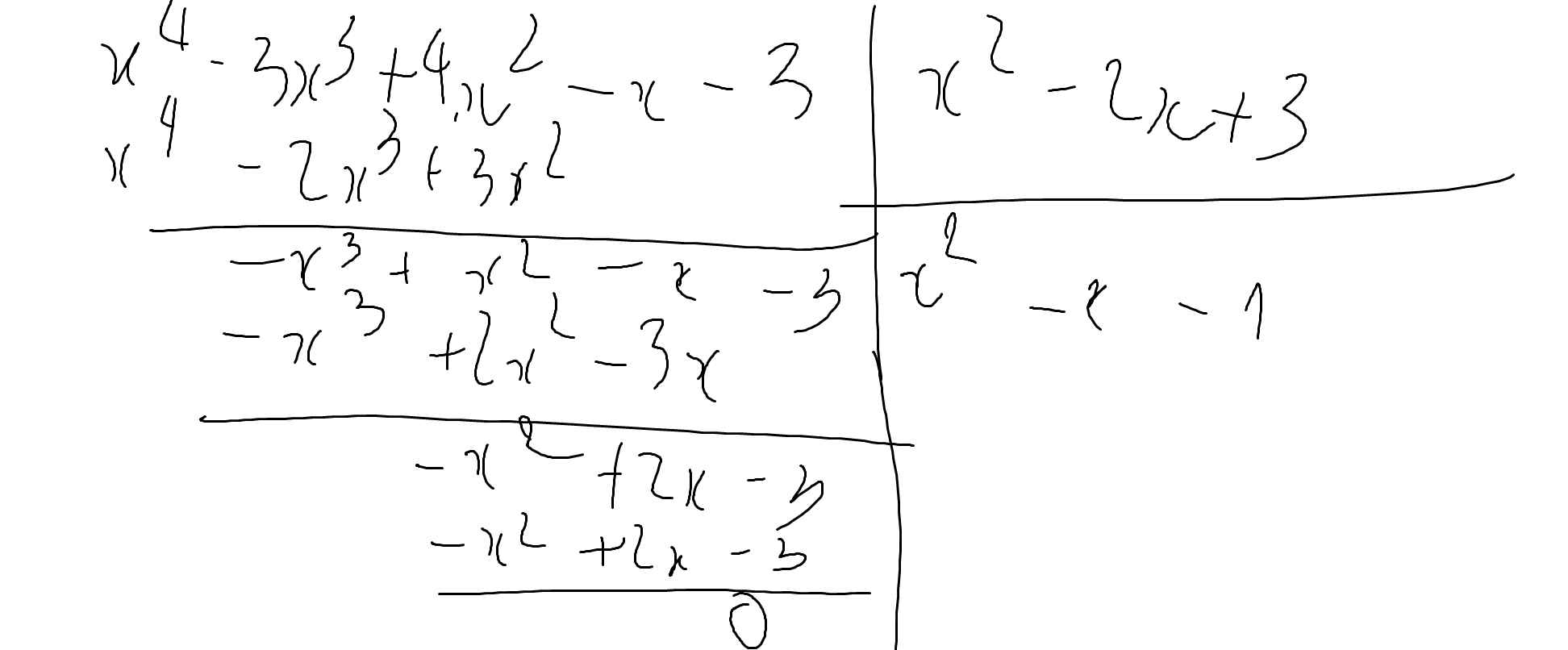
c:
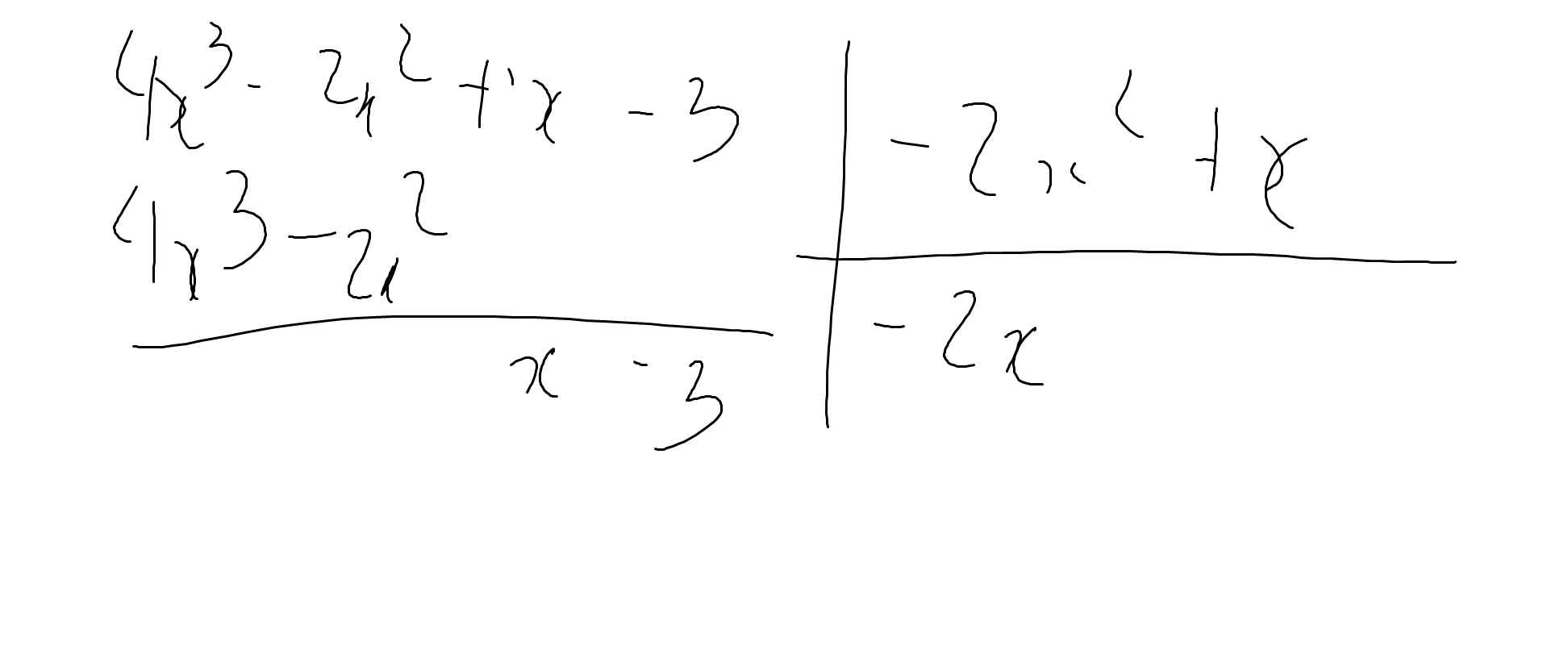
d:
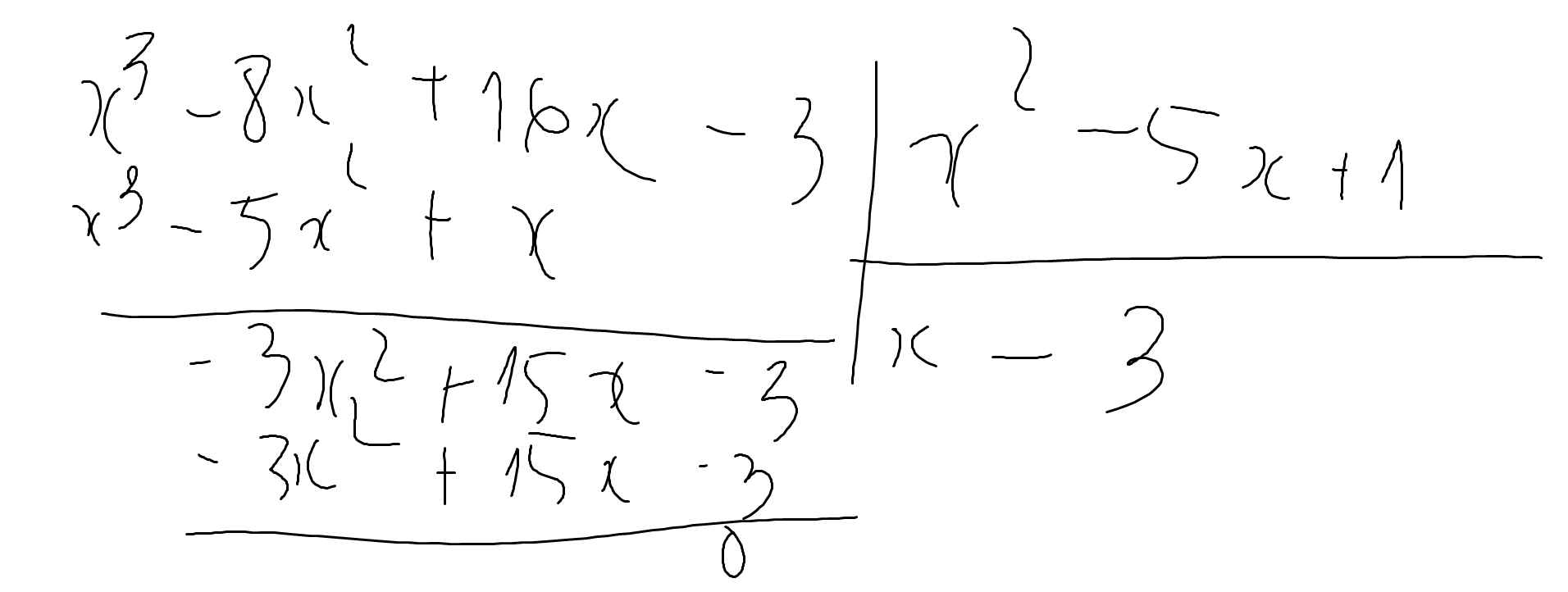
Bài 4:
a: \(A\left(x\right)=x^7-3x^2-x^5+x^4-x^2+2x-7\)
\(=x^7-x^5+x^4+\left(-3x^2-x^2\right)+2x-7\)
\(=x^7-x^5+x^4-4x^2+2x-7\)
\(B\left(x\right)=x-2x^2+x^4-x^5-x^7-4x^2-1\)
\(=-x^7-x^5+x^4+\left(-2x^2-4x^2\right)+x-1\)
\(=-x^7-x^5+x^4-6x^2+x-1\)
b: A(x)+B(x)
\(=x^7-x^5+x^4-4x^2+2x-7-x^7-x^5+x^4-6x^2+x-1\)
\(=-2x^5-10x^2+3x-8\)
A(x)-B(x)
\(=x^7-x^5+x^4-4x^2+2x-7+x^7+x^5-x^4+6x^2-x+1\)
\(=2x^7+2x^2+x-6\)
c: C(x)=A(x)+B(x
=>\(C\left(x\right)=-2x^5-10x^2+3x-8\)
Thay x=-1 vào C(x), ta được:
\(C\left(-1\right)=-2\cdot\left(-1\right)^5-10\cdot\left(-1\right)^2+3\cdot\left(-1\right)-8\)
=2-10-3-8
=-1-10-8=-19

a, Ta có DE vuông AB
AH vuông AB
=> DE // AH
b, Ta có DE // AH => ^BDE = ^ACB ( 2 góc đồng vị )
=> ^BDE = ^DCH = 400
c, Ta có DH vuông AC
AB vuông AC
=> DH // AB
Ta có DH // AB; ED//AH ; ^EAH = ^AED = ^AHD = 900
Vậy tứ giác AEDH là hình vuông
=> DE vuông DH

a: ta có: \(\widehat{MNS}=\widehat{HNQ}\)(hai góc đối đỉnh)
mà \(\widehat{HNQ}=60^0\)
nên \(\widehat{MNS}=60^0\)
b: Ta có: \(\widehat{QNH}=\widehat{PMN}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên PI//QS
=>MP//NQ
c: ta có: MP//NQ
KP\(\perp\)MP
Do đó: KP\(\perp\)QN
d: ta có: MI//SN
=>\(\widehat{MIS}+\widehat{S}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{S}+100^0=180^0\)
=>\(\widehat{S}=80^0\)

a) Ta có:
\(VT=\left(a+b\right)^2-4ab=\left(a^2+2ab+b^2\right)-4ab\\ =a^2+2ab+b^2-4ab=a^2-2ab+b^2\\ =\left(a-b\right)^2=VP\)
=> Đpcm
b) Ta có:
\(VT=\left(a-b\right)^3=\left[-\left(b-a\right)\right]^3=\left[\left(-1\right)\cdot\left(b-a\right)\right]^3\\ =\left(-1\right)^3\left(b-a\right)^3=\left(-1\right)\cdot\left(b-a\right)^3=-\left(b-a\right)^3=VP\)
=> Đpcm
c) Ta có:
\(\left(n+2\right)^2-n^2=\left(n^2+4n+4\right)-n^2\\ =n^2+4n+4-n^2=4n+4=4\left(n+1\right)⋮4\forall n\in N\)
=> Đpcm
a: \(\left(a+b\right)^2-4ab\)
\(=a^2+2ab+b^2-4ab\)
\(=a^2-2ab+b^2=\left(a-b\right)^2\)
b: \(\left(a-b\right)^3=\left[-\left(b-a\right)\right]^3=-\left(b-a\right)^3\)
c: \(\left(n+2\right)^2-n^2=\left(n+2+n\right)\left(n+2-n\right)\)
\(=2\left(2n+2\right)=4\left(n+1\right)⋮4\)
\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{23}+\dfrac{1}{6}\\ =\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\dfrac{1}{23}+\dfrac{1}{6}\\ =\dfrac{1}{6}+\dfrac{1}{23}+\dfrac{1}{6}\\ =\dfrac{2}{6}+\dfrac{1}{23}\\ =\dfrac{1}{3}+\dfrac{1}{23}\\ =\dfrac{26}{69}\)