Nhanh nhé
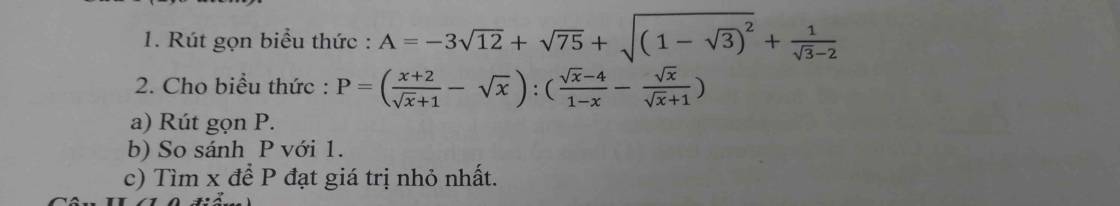
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Thay m=7 vào (d), ta được:
\(y=5x-7+3=5x-4\)
Phương trình hoành độ giao điểm là:
\(x^2=5x-4\)
=>\(x^2-5x+4=0\)
=>(x-1)(x-4)=0
=>\(\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Khi x=1 thì \(y=1^2=1\)
Thay x=4 vào (P), ta được:
\(y=4^2=16\)
vậy: (d) giao (P) là A(1;1); B(4;16)

a: \(2x^3+3x^2-3x-2=0\)
=>\(\left(2x^3-2\right)+\left(3x^2-3x\right)=0\)
=>\(2\left(x-1\right)\left(x^2+x+1\right)+3x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x^2+2x+2+3x\right)=0\)
=>\(\left(x-1\right)\left(2x^2+4x+x+2\right)=0\)
=>(x-1)(x+2)(2x+1)=0
=>\(\left[{}\begin{matrix}x=1\\x=-2\\x=-\dfrac{1}{2}\end{matrix}\right.\)
b: \(x^3+1-\left(x+1\right)\left(x^2-5\right)=0\)
=>\(\left(x+1\right)\left(x^2-x+1\right)-\left(x+1\right)\left(x^2-5\right)=0\)
=>\(\left(x+1\right)\left(x^2-x+1-x^2+5\right)=0\)
=>(x+1)(6-x)=0
=>\(\left[{}\begin{matrix}x=-1\\x=6\end{matrix}\right.\)
c: \(x^3+2x^2-x-2=0\)
=>\(x^2\left(x+2\right)-\left(x+2\right)=0\)
=>\(\left(x+2\right)\left(x^2-1\right)=0\)
=>(x+2)(x-1)(x+1)=0
=>\(\left[{}\begin{matrix}x=-2\\x=-1\\x=1\end{matrix}\right.\)
d: \(x^2-x-2=0\)
=>\(x^2-2x+x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
e: Sửa đề: \(x^2+2x-15=0\)
=>\(x^2+5x-3x-15=0\)
=>x(x+5)-3(x+5)=0
=>(x+5)(x-3)=0
=>\(\left[{}\begin{matrix}x=-5\\x=3\end{matrix}\right.\)
f: \(4x^2-12x+5=0\)
=>\(4x^2-10x-2x+5=0\)
=>2x(2x-5)-(2x-5)=0
=>(2x-5)(2x-1)=0
=>\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)

Hiệu số phần bằng nhau là 5-3=2(phần)
Hiệu vận tốc của hai xe là 48:3=16(km/h)
Vận tốc của ô tô đi từ A là 16:2x5=40(km/h)
Vận tốc của ô tô đi từ B là 40-16=24(km/h)
Độ dài quãng đường BC là:
24x3=72(km)

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
\(\widehat{KBN}\) là góc tạo bởi tiếp tuyến BK và dây cung BN
\(\widehat{BCN}\) là góc nội tiếp chắn cung BN
Do đó: \(\widehat{KBN}=\widehat{BCN}\)
Xét ΔKBN và ΔKCB có
\(\widehat{KBN}=\widehat{KCB}\)
\(\widehat{BKN}\) chung
Do đó: ΔKBN~ΔKCB
=>\(\dfrac{KB}{KC}=\dfrac{KN}{KB}\)
=>\(KB^2=KN\cdot KC\)
b: Ta có: \(KB^2=KN\cdot KC\)
KB=KA
Do đó: \(KA^2=KN\cdot KC\)
=>\(\dfrac{KA}{KN}=\dfrac{KC}{KA}\)
Xét ΔKAC và ΔKNA có
\(\dfrac{KA}{KN}=\dfrac{KC}{KA}\)
\(\widehat{AKC}\) chung
Do đó: ΔKAC~ΔKNA
=>\(\widehat{KCA}=\widehat{KAN}\)
Xét (O) có
\(\widehat{NCA}\) là góc tạo bởi tiếp tuyến CA và dây cung CN
\(\widehat{NMC}\) là góc nội tiếp chắn cung CN
Do đó: \(\widehat{NCA}=\widehat{NMC}\)
=>\(\widehat{NMC}=\widehat{NAK}\)
=>AB//CM
Dựa vào thông tin đã được cung cấp, chúng ta có thể chứng minh như sau:
a) Chứng minh: OA vuông góc BC tại H và BK^2=KN.KC
b) Chứng minh: MC//AB
Tóm lại, dựa vào thông tin đã cung cấp, chúng ta có thể chứng minh a) và b) theo yêu cầu của câu hỏi.

7 lần số chia là 234-3=231
Số chia là 231:7=33
Số bị chia là 234-33=201

3. Phương trình có hai nghiệm phân biệt khi:
\(\Delta'=\left(m-1\right)^2-\left(4m-11\right)>0\)
\(\Leftrightarrow m^2-6m+12>0\Leftrightarrow\left(m-3\right)^2+3>0\) (luôn đúng).
Do đó, phương trình có hai nghiệm phân biệt với mọi \(m.\)
Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2-2m\\x_1x_2=\dfrac{c}{a}=4m-11\end{matrix}\right.\)
Theo đề: \(2\left(x_1-1\right)^2+\left(6-x_2\right)\left(x_1x_2+11\right)=72\)
\(\Leftrightarrow2\left(x_1^2-2x_1+1\right)+\left(6-x_2\right)\left(4m-11+11\right)=72\)
Do \(x_1\) là nghiệm của phương trình nên:
\(x_1^2+2\left(m-1\right)x_1+4m-11=0\Leftrightarrow x_1^2=-2\left(m-1\right)x_1-4m+11\)
Suy ra: \(-2\left(m-1\right)x_1-4m+11-2x_1+1+2m\left(6-x_2\right)=36\)
\(\Leftrightarrow-m\left(x_1+x_2\right)+4m=12\)
\(\Rightarrow-m\left(2-2m\right)+4m=12\)
\(\Leftrightarrow2m^2+2m-12=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-3\end{matrix}\right.\)

Độ dài mới của đáy là 35+4=39(m)
Diện tích ban đầu là:
\(15,2:4\times35=133\left(m^2\right)\)

Tuổi anh hơn TBC của tuổi hai anh em là 4 tuổi nên suy ra tuổi anh hơn tuổi em 8 tuổi
1: \(A=-3\sqrt{12}+\sqrt{75}+\sqrt{\left(1-\sqrt{3}\right)^2}+\dfrac{1}{\sqrt{3}-2}\)
\(=-6\sqrt{3}+5\sqrt{3}+\sqrt{3}-1-\dfrac{1}{2-\sqrt{3}}\)
\(=-1-\dfrac{\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=-1-2-\sqrt{3}=-3-\sqrt{3}\)
2:
a: \(P=\left(\dfrac{x+2}{\sqrt{x}+1}-\sqrt{x}\right):\left(\dfrac{\sqrt{x}-4}{1-x}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{x+2-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}:\left(\dfrac{-\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{-\sqrt{x}+2}{\sqrt{x}+1}:\dfrac{-\sqrt{x}+4-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{-\sqrt{x}+4-x+\sqrt{x}}\)
\(=\dfrac{-\sqrt{x}+2}{1}\cdot\dfrac{\sqrt{x}-1}{-x+4}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
b: \(P-1=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-1=\dfrac{\sqrt{x}-1-\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{-3}{\sqrt{x}+2}< 0\)
=>P<1