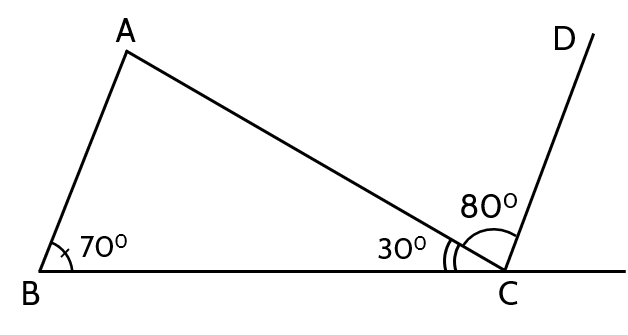
(0,75 điểm) Hãy chứng tỏ trong hình vẽ trên có$AB$ // $CD$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ dài quãng đường đó là 1,609344×200=321,8688 km
Làm tròn kết quả với độ chính xác 0,5 là 322 km
Độ dài quãng đường từ sân vận động Old Trafford đến tháp đồng hồ Big Ben là 200.1,609344=321,8688200.1,609344=321,8688 km.
Để kết quả có độ chính xác 0,50,5 ta cần làm tròn 321,8688321,8688 đến chữ số thập phân thứ nhất, kết quả là 321,8688≈321,9321,8688≈321,9 km.

(-0,25 )5 : \(x\) = (-0,25)3
\(x\) = (-0,25)5 : (-0,25)3
\(x\) = (-0,25)2
\(x\) = 0,0625

0,75 + \(\dfrac{9}{5}\) ( 1,5 - \(\dfrac{2}{3}\) )2
= 0,75 + \(\dfrac{9}{5}\) ( \(\dfrac{3}{2}\) - \(\dfrac{2}{3}\))2
= 0,75 + \(\dfrac{9}{5}\) (\(\dfrac{5}{6}\))2
= 0,75 + \(\dfrac{5}{4}\)
= 0,75 + 1,25
= 2
\(\dfrac{-22}{25}\) + ( \(\dfrac{22}{7}\) - 0,12)
= \(\dfrac{-22}{25}\) + ( \(\dfrac{22}{7}\) - \(\dfrac{3}{25}\))
= \(\dfrac{-22}{25}\) + \(\dfrac{22}{7}\) - \(\dfrac{3}{25}\)
= - ( \(\dfrac{22}{25}\) + \(\dfrac{3}{25}\)) + \(\dfrac{22}{7}\)
= -1 + \(\dfrac{22}{7}\)
= \(\dfrac{-7}{7}\) + \(\dfrac{22}{7}\)
= \(\dfrac{15}{7}\)
a) \dfrac{3}{4}+\dfrac{9}{5}\left(\dfrac{3}{2}-\dfrac{2}{3}\right)^2=\dfrac{3}{4}+\dfrac{9}{5}\left(\dfrac{5}{6}\right)^2=\dfrac{3}{4}+\dfrac{9}{5} \cdot \dfrac{25}{36}=\dfrac{3}{4}+\dfrac{5}{4}=243+59(23−32)2=43+59(65)2=43+59⋅3625=43+45=2
b) \dfrac{-22}{25}+\left(\dfrac{22}{7}-0,12\right) =\dfrac{-22}{25}+\left(\dfrac{22}{7}-\dfrac{12}{100}\right)=\dfrac{-88}{100}+\dfrac{22}{7}+\dfrac{-12}{100} =\left(\dfrac{-88}{100}+\dfrac{-12}{100}\right)+\dfrac{22}{7}=-1+\dfrac{22}{7}=\dfrac{15}{7}25−22+(722−0,12) =25−22+(722−10012)=100−88+722+100−12 =(100−88+100−12)+722=−1+722=715

Số tiền thưởng của tổ 1 là:
\(\dfrac{182}{3+4+5}x3=\dfrac{182}{12}x3=\dfrac{91}{6}x3=\dfrac{91}{2}=45,5\) (triệu đồng)
Số tiền thưởng của tổ 2 là:
\(\dfrac{182}{3+4+5}x4=\dfrac{182}{12}x4=\dfrac{182}{3}=60,67\) (triệu đồng)
Số tiền thưởng của tổ 3 là:
\(\dfrac{182}{3+4+5}x5=\dfrac{182}{12}x5=\dfrac{91}{6}x5=\dfrac{91}{2}=75,83\) (triệu đồng)

x^2+1=0
x^2= 0-1
x^2=-1
Vậy x không xảy ra vì biệt số có giá trị âm


Em nên gõ công thức trực quan để đề bài được rõ ràng nhé


`(x-1)^{2020}=(x-1)^{2022}`
`<=>(x-1)^{2022}-(x-1)^{2020}=0`
`<=>(x-1)^{2020}[(x-1)^{2}-1]=0`
`@TH1: (x-1)^{2020}=0<=>x-1=0<=>x=1`
`@TH2: (x-1)^{2}-1=0<=>(x-1)^{2}=1`
`<=>x-1=1` hoặc `x-1=-1`
`<=>x=2` hoặc `x=0`
\(\left(x-1\right)^{2020}=\left(x-1\right)^{2022}\)
⇒\(\left(x-1\right)^{2020}-\left(x-1\right)^{2022}=0\)
⇒\(\left(x-1\right)^{2020}\cdot\left[1-\left(x-1\right)^2\right]=0\)
+) \(\left(x-1\right)^{2020}=0\)
\(\Leftrightarrow x=1\)
+) \(1-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)^2=1\)
\(\Leftrightarrow x-1=1hoặcx-1=-1\)
\(\Leftrightarrow x=2hoặcx=0\)
Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD