
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:
| Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
| Xuất khẩu | 63,4 | 78,56 | 89,1 |
| Nhập khẩu | 59,59 | 76,1 | 87,64 |
b:
| Giai đoạn | Quý I/2020 | Quý I/2021 | Quý I/2022 |
| Tỉ số giữa xuất và nhập | 1,06 | 1,03 | 1,01 |
c: Tổng trị giá xuất khẩu của nước ta trong quý I giai đoạn 2020-2022 là:
63,4+78,56+89,1=231,06(tỉ USD)
d: Tổng trị giá nhập khẩu của nước ta trong quý I giai đoạn 2020-2022 là:
59,59+76,1+87,64=223,33(tỉ USD)
e: Trị giá xuất khẩu trong quý I/2020 so với quý I/2021 thì giảm:
\(\dfrac{78,56-63,4}{63,4}\simeq23,91\%\)
f: Trị giá nhập khẩu trong quý I/2021 so với quý I/2020 thì tăng:
\(\dfrac{76,1-59,59}{59,59}-100\%\simeq27.71\%\)

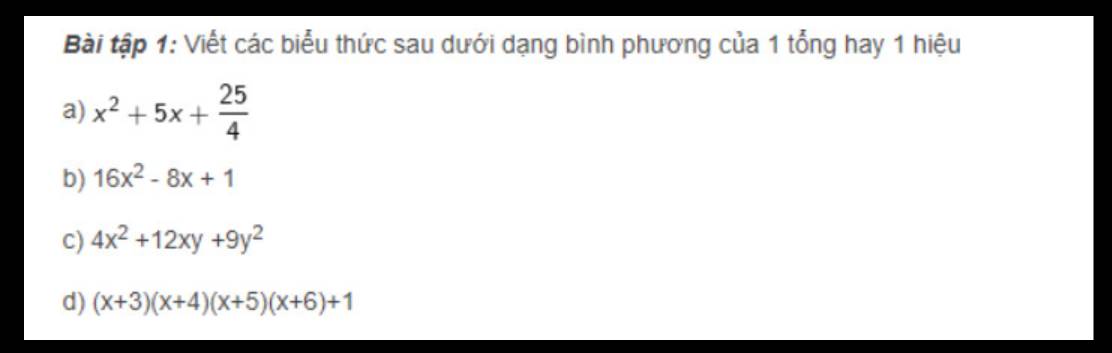
a)
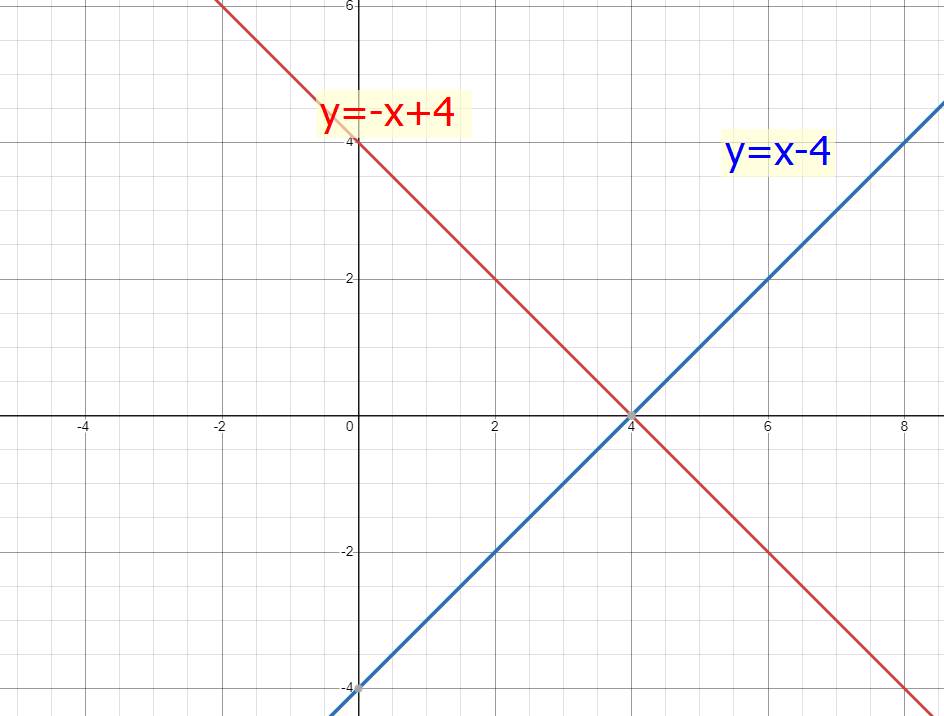
b) Hàm số y=-x+4 cắt Oy tại \(\left(0;4\right)\) \(\Rightarrow A\left(0;4\right)\)
Hàm số y=x-4 cắt Oy tại \(\left(0;-4\right)\) \(\Rightarrow B\left(0;-4\right)\)
Ta có pt hoành độ giao điểm của y=-x+4 và y=x-4 là:
\(-x+4=x-4\Leftrightarrow x=4\)
\(\Rightarrow y=4-4=0\)
\(\Rightarrow C\left(4;0\right)\)
c) Ta có: \(A\left(0;4\right)\Rightarrow OA=4\)
\(B\left(0;-4\right)\Rightarrow OB=4\)
\(C\left(0;4\right)\Rightarrow OC=4\)
BC = OA + OB = 4 + 4 = 8
\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot4\cdot8=16\) (đvdt)

a: Xác suất thực nghiệm của biến cố "Thẻ lấy ra ghi số 7" là:
\(\dfrac{6}{30}=\dfrac{1}{5}\)
b: Gọi A là biến cố "Thẻ rút ra là số nguyên tố"
=>A={2;3;5;7;11;13}
=>n(A)=6
=>\(P_A=\dfrac{6}{15}=\dfrac{2}{5}\)
=>Khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố A ngày càng gần với 2/5

a: \(x^2+5x+\dfrac{25}{4}=x^2+2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2=\left(x+\dfrac{5}{2}\right)^2\)
b: \(16x^2-8x+1=\left(4x\right)^2-2\cdot4x\cdot1+1^2=\left(4x-1\right)^2\)
c: \(4x^2+12xy+9y^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2=\left(2x+3y\right)^2\)
d: \(\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)+1\)
\(=\left(x^2+9x+18\right)\left(x^2+9x+20\right)+1\)
\(=\left(x^2+9x\right)^2+38\left(x^2+9x\right)+360+1\)
\(=\left(x^2+9x\right)^2+2\cdot\left(x^2+9x\right)\cdot19+19^2\)
\(=\left(x^2+9x+19\right)^2\)

1: Xét ΔDIN vuông tại I và ΔDKP vuông tại K có
\(\widehat{IDN}=\widehat{KDP}\)(hai góc đối đỉnh)
Do đó: ΔDIN~ΔDKP
2: Xét ΔMIN vuông tại I và ΔMKP vuông tại K có
\(\widehat{IMN}=\widehat{KMP}\)
Do đó: ΔMIN~ΔMKP
=>\(\dfrac{MI}{MK}=\dfrac{MN}{MP}\)
=>\(MI\cdot MP=MN\cdot MK\)

\(\dfrac{\left(x-2\right)^2}{3}-\dfrac{\left(2x-3\right)\left(2x+3\right)}{8}+\dfrac{\left(x-4\right)^2}{6}=0\)
=>\(\dfrac{8\left(x-2\right)^2-3\left(2x-3\right)\left(2x+3\right)+4\left(x-4\right)^2}{24}=0\)
=>\(8\left(x^2-4x+4\right)-3\left(4x^2-9\right)+4\left(x^2-8x+16\right)=0\)
=>\(8x^2-32x+32-12x^2+27+4x^2-32x+64=0\)
=>-64x+123=0
=>\(x=\dfrac{123}{64}\)

a: (2m-4)x+2-m=0
=>x(2m-4)=m-2
TH1: m=2
Phương trình sẽ trở thành \(x\left(2\cdot2-4\right)=2-2\)
=>0x=0(luôn đúng)
=>Phương trình có vô số nghiệm
TH2: \(m\ne2\)
Phương trình sẽ tương đương với \(x=\dfrac{m-2}{2m-4}=\dfrac{1}{2}\)
b: \(\left(m+1\right)x=\left(3m^2-1\right)x+m-1\)
=>\(\left(m+1\right)x-\left(3m^2-1\right)x=m-1\)
=>\(x\left(m+1-3m^2+1\right)=m-1\)
=>\(x\left(-3m^2+m+2\right)=m-1\)
=>\(x\left(-3m^2+3m-2m+2\right)=m-1\)
=>\(x\cdot\left(m-1\right)\left(-3m-2\right)=m-1\)
TH1: m=1
Phương trình sẽ trở thành \(x\left(1-1\right)\left(-3\cdot1-2\right)=1-1\)
=>0x=0(luôn đúng)
=>Phương trình có vô số nghiệm
TH2: m=-2/3
Phương trình sẽ trở thành:
\(x\left(-\dfrac{2}{3}-1\right)\left(-3\cdot\dfrac{-2}{3}-2\right)=\dfrac{-2}{3}-1\)
=>0x=-5/3(vô lý)
=>Phương trình vô nghiệm
TH3: \(m\notin\left\{1;-\dfrac{2}{3}\right\}\)
Phương trình sẽ tương đương với \(x=\dfrac{m-1}{\left(m-1\right)\left(-3m-2\right)}=\dfrac{-1}{3m+2}\)
c: \(ax+2m=a+x\)
=>ax-x=a-2m
=>x(a-1)=a-2m
TH1: a=1
Phương trình sẽ trở thành:
x(1-1)=1-2m
=>0x=1-2m
-Nếu \(m=\dfrac{1}{2}\) thì 0x=1-2*1/2=0
=>Phương trình có vô số nghiệm
Nếu \(m\ne\dfrac{1}{2}\) thì phương trình vô nghiệm
TH2: a<>1
Phương trình sẽ tương đương với \(x=\dfrac{a-2m}{a-1}\)

a: \(3x+\left(-5+x\right)=7-\left(5x-4\right)\)
=>3x-5+x=7-5x+4
=>4x-5=-5x+11
=>9x=16
=>\(x=\dfrac{16}{9}\)
b: Đề thiếu vế phải rồi bạn
c: \(2\left(x+5\right)-9x=12-4\left(2x-3\right)\)
=>2x+10-9x=12-8x+12
=>-7x+10=-8x+24
=>-7x+8x=24-10
=>x=14
d: \(x-\left(3x+1\right)=-\left(x+1\right)+21\)
=>x-3x-1=-x-1+21
=>-2x-1=-x+20
=>-2x+x=20+1
=>-x=21
=>x=-21

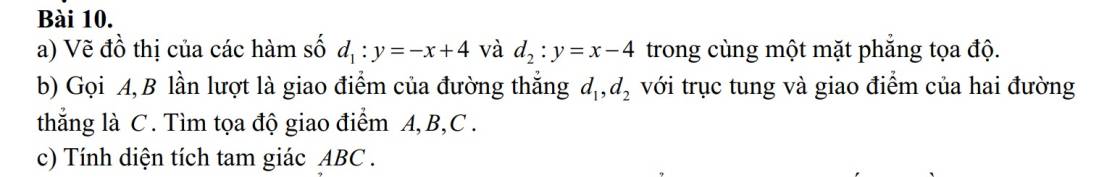
Tự vẽ hình nhé.
a) Theo bài ra ABCD là HCN
=> AD=BC (1) ; AD//BC
Do AD//BC => ADB=DBC (2 góc so le trong) hay ADN=CBM (2)
Ta có AN vuông góc với BD => AND=ANB=90
CM vuông góc với BD => CMD=CMB=90
Xét tam giác AND và tam giác CMB có
AND=CMB=90
AD=BC ( theo (1) )
ADN = CBM ( theo (2) )
=> tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> ND = MB (2 cạnh tương ứng) (dpcm)
b) Do AN vuông góc với BD và CM vuông góc với BD
=>AN//CM (mối quan hệ từ vuông góc đến song song)
Lại có: tam giác AND= tam giác CMB (cạnh huyền-góc nhọn)
=> AN = CM (2 cạnh tương ứng)
Xét tứ giác ANCM có AN=CM và AN//CM
=> tứ giác ANCM là hình bình hành.
c) Lại thấy AN//CM => KN // CM
Xét tứ giác KCMN có KN=CM và KN // CM
=> tứ giác KCMN là hình bình hành
=> KC // MN
=> KC//BD
Xét tứ giác DKCB có KC//BD => tứ giác DKCB là hình thang.
d) Do K là điểm đối xứng với A qua N
=>NA=NK
=> N là trung điểm của AK.
=>PN là đường trung tuyến của tam giác AKP.
Mặt khác KC//MN => CP//MB => BMP= MPC (2 góc so le trong)
Mà AMN=BMP (2 góc đồng vị)
Từ đó suy ra AMN=MPC
Vì ANM=90 nên tam giác ANM vuông tại N
=> NAM +AMN = 90
Vì MC vuông góc với BD mà BD//CP
=> MC vuông góc với CP (mqh..)
=> MCP = 90 => tam giác MCP vuông tại C => CMP+MPC=90
Do đó NAM + AMN = CMP + MPC = 90
Mà AMN=MPC
=> NAM = CMP
Xét tam giác ANM và tam giác MCP có
NAM = CMP (theo cmt)
AN=CM (từ phần b)
ANM=MCP(=90)
=> tam giác ANM = tam giác MCP (cạnh huyền-cạnh góc vuông)
=> AN=MP( 2 cạnh tương ứng)
và MN =CP ( 2 cạnh tương ứng)
Vì MN=CK và MN=CP
=> CK=CP
=> C là trung điểm của PK
=>AC là đường trung tuyến của tam giác AKP.
Do AM=MP => M là trung điểm của AP
=>KM là đường trung tuyến của tam giác AKP.
Xét tam giác AKP có PN là đường trung tuyến của tam giác AKP.
AC là đường trung tuyến của tam giác AKP.
KM là đường trung tuyến của tam giác AKP.
Từ đó suy ra PN, AC, KM đồng quy tại trọn tâm của tam giác AKP
Vậy..