125.(-3).(-8).(-10) lời giả chi tiết
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Vì $p>3$ và $p$ là snt nên $p$ không chia hết cho $3$. Do đó $p=3k+1$ hoặc $p=3k+2$ với $k$ là số tự nhiên.
Nếu $p=3k+2$ thì $p+4=3k+6=3(k+2)\vdots 3$ và $p+4>3$ nên $p+4$ không là số nguyên tố (trái với đề)
$\Rightarrow p=3k+1$
$\Rightarrow p+8=3k+9=3(k+3)\vdots 3$. Mà $p+8>3$ nên $p+8$ là hợp số (đpcm)

Giải thích:
Để so sánh giá trị của biểu thức A với 3/2, ta cần tính giá trị của biểu thức A và so sánh nó với giá trị của 3/2.
Lời giải:
Để tính giá trị của biểu thức A, ta thực hiện các bước sau:
1. Tính tử số và mẫu số của từng phân số trong biểu thức A.
2. Tính giá trị của từng phân số.
3. Cộng tất cả các giá trị đã tính được.
Đầu tiên, ta tính tử số và mẫu số của từng phân số trong biểu thức A:
- Tử số của phân số thứ nhất là 4, mẫu số là 1.2.3.
- Tử số của phân số thứ hai là 6, mẫu số là 2.3.4.
- Tử số của phân số thứ ba là 8, mẫu số là 3.4.5.
- ...
- Tử số của phân số cuối cùng là 200, mẫu số là 99.100.11.
Tiếp theo, ta tính giá trị của từng phân số:
- Giá trị của phân số thứ nhất là 4/(1.2.3) = 4/6 = 2/3.
- Giá trị của phân số thứ hai là 6/(2.3.4) = 6/24 = 1/4.
- Giá trị của phân số thứ ba là 8/(3.4.5) = 8/60 = 2/15.
- ...
- Giá trị của phân số cuối cùng là 200/(99.100.11).
Cuối cùng, ta cộng tất cả các giá trị đã tính được:
A = (2/3) + (1/4) + (2/15) + ... + (200/(99.100.11)).
Sau khi tính giá trị của biểu thức A, ta so sánh nó với giá trị của 3/2 để xác định mối quan hệ giữa chúng.
Tra bài tập tại Checkmath là ra
😀😀

Bài 11
a) 5²⁰¹⁹ - 5²⁰²⁰ + 5²⁰²¹
= 5²⁰¹⁹.(1 - 5 + 5²)
= 5²⁰¹⁹.21
= 3.7.5²⁰¹⁹ ⋮ 3
Vậy (5²⁰¹⁹ - 5²⁰²⁰ + 5²⁰²¹) ⋮ 3
b) 4³⁹ - 4⁴⁰ + 4⁴¹
= 4³⁸.(4 - 4² + 4³)
= 4³⁸.(4 - 16 + 64)
= 4³⁸.52
= 2.26.4³⁸ ⋮ 26
Vậy (4³⁹ - 4⁴⁰ + 4⁴¹) ⋮ 26
c) Đặt C = 1 + 7 + 7² + ... + 7²⁰²¹
= (1 + 7) + (7² + 7³) + ... + (7²⁰²⁰ + 7²⁰²¹)
= 8 + 7².(1 + 7) + ... + 7²⁰²⁰.(1 + 7)
= 8 + 7².8 + ... + 7²⁰²⁰.8
= 8.(1 + 7² + ... + 7²⁰²⁰) 8
Vậy C 8
C = 1 + 7 + 7² + ... + 7²⁰²¹
= (1 + 7 + 7²) + (7³ + 7⁴ + 7⁵) + ... + (7²⁰¹⁹ + 7²⁰²⁰ + 7²⁰²¹)
= 57 + 7³.(1 + 7 + 7²) + ... + 7²⁰¹⁹.(1 + 7 + 7²)
= 57 + 7³.57 + ... + 7²⁰¹⁹.57
= 57.(1 + 7³ + ... + 7²⁰¹⁹)
= 19.3.(1 + 7³ + ... + 7²⁰¹⁹) ⋮ 19
Vậy C ⋮ 19
Bài 10
Các số nguyên âm chẵn có một chữ số:
-2; -4; -6; -8
A = (-2).(-4).(-6).(-8) = 384
Các số nguyên dương có hai chữ số nhỏ hơn 20:
10; 11; 12; 13; 14; 15; 16; 17; 18; 19
B = 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19
= 145
A - B = 384 - 145 = -239

Lời giải:
Theo đề thì $x=BCNN(30,40), x\neq 0$
Có: $30=2.3.5$
$40=2^3.5$
$\Rightarrow x=BCNN(30,40)=2^3.3.5=120$

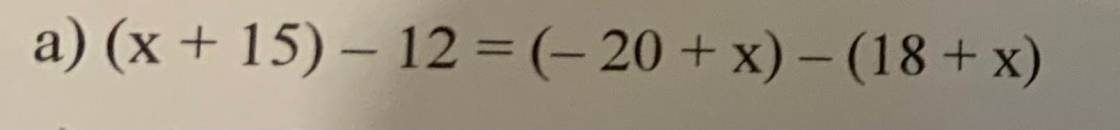

125.(-3).(-8).(-10)
= [125.(-8)].[(-3).(-10)]
= -1000.30
= -30000