
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau 1 ngày: 1×2=2 ( cây bèo )
cây bèo.
Sau 2 ngày: 2×2=4 ( cây bèo )
Sau 3 ngày: 4×2=8 ( cây bèo )
Số ngày cần để 8 cây bèo phủ kín mặt ao là: 35−3=32 ( ngày )
Vậy sau 32 ngày, mặt ao sẽ được phủ kín bèo.

ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn tâm O, đường kính BC
=>O là trung điểm của BC
Vì OA=OC
nên O nằm trên đường trung trực của AC
=>OD là đường trung trực của AC
=>OD\(\perp\)AC
mà AB\(\perp\)AC
nên OD//AB
=>\(\widehat{ODB}=\widehat{ABD}\)
mà \(\widehat{ABD}=\widehat{OBD}\)(BD là phân giác của góc ABC)
nên \(\widehat{OBD}=\widehat{ODB}\)
=>OB=OD=R
=>D thuộc đường tròn ngoại tiếp ΔABC

Câu 8: Số tiền con thứ hai nhận được là:
8400000x125%=10500000(đồng)
Số tiền con thứ nhất nhận được là:
10500000x50%=5250000(đồng)
Số tiền con thứ ba nhận được là:
5250000+8400000=13650000(đồng)
Số tiền con thứ ba nhận được hơn con thứ hai là:
13650000-10500000=3150000(đồng)
Câu 9: Từ khi đoàn tàu đi vào hầm đến khi đoàn tàu chui ra khỏi hầm đoàn tàu đã đi quãng đường là:
0,55 + 0,25 = 0,8 (km)
Thời gian đoàn tầu xuyên qua đường hầm là:
0,8 : 80 = \(\dfrac{1}{100}\) (giờ)
\(\dfrac{1}{100}\) giờ = 36 giây
Đáp số: 36 giây.

Ta có thể thấy: 1+4 = 5, 5+4 = 9, 9+4 = 13...
Vậy 2 số còn lại sẽ là: 13+4 = 17 và 17+4 =21
2 số còn thiếu là: 17 và 21
Tick cho c vs nhé !!!

\(\dfrac{2}{9}\times\dfrac{3}{5}+\dfrac{6}{11}+\dfrac{13}{9}\times\dfrac{3}{5}+\dfrac{5}{11}\)
\(=\dfrac{3}{5}\times\left(\dfrac{2}{9}+\dfrac{13}{9}\right)+1\)
\(=\dfrac{3}{5}\times\dfrac{15}{9}+1=1+1=2\)

2 lần số trận thắng là: \(\dfrac{1800000}{200000}+15=24\)
=>Số trận thắng là 24:2=12(trận)
Giả sử tất cả các trận đều thắng thì số tiền thưởng là
200 000 . 15 = 3000 000 (đồng)
Giả sử thay một trận thắng bằng 1 trận thua thì số tiền mất đi là
200 000 + 200 000 = 400 000 (đồng)
Số trận thua là
(3000 000 - 1800 000) : 400 000 = 3 (trận)
Vậy đội đó thắng số trận là
15 -3 = 12 (trận)
Đáp số ....

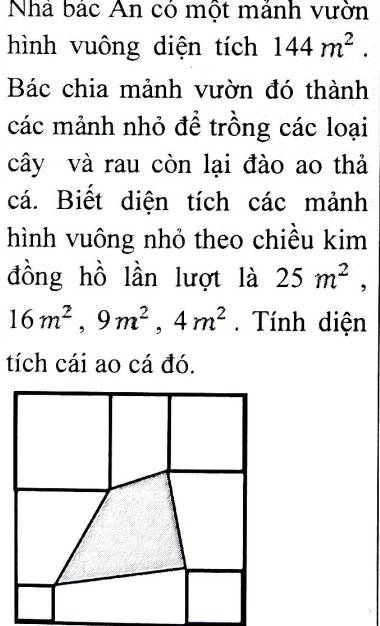
Ta đánh số các hình như hình minh họa khi đó ta có:
Vì 144 = 12 x 12
Vậy cạnh hình vuông mảnh đất là 12 m
25 = 5 x 5; 16 = 4 x 4 ; 9 = 3 x 3; 4 = 2 x 2
Vậy cạnh hình vuông của các mảnh đất nhỏ theo thứ tự chiều kim đồng hồ lần lượt là:
5m; 4m; 3m; 2m
Chiều cao của hình thang thứ nhất:
12 - 5 - 4 = 3 (m)
Chiều cao của hình thang thứ hai là:
12 - 4 - 3 = 5(m)
Chiều cao của hình thang thứ tư là:
12 - 3 - 2 = 7 (m)
Diện tích hình thang thứ nhất là:
(5 + 4) x 3 : 2 = 13,5 (m2)
Diện tích hình thang thứ hai là:
(4 + 3) x 5 : 2 = 17,5 (m2)
Diện tích hình thang thứ ba là:
(3 + 2) x 7: 2 = 17,5 (m2)
Diện tích hình thang thứ tư là:
(2 + 5) x 5 : 2 = 17,5 (m2)
Diện tích ao cá là:
144 - 13,5 - 17,5 - 17,5 - 17,5 = 78 (m2)
Đáp số: 78 m2

\(3n+5⋮n-3\)
=>\(3n-9+14⋮n-3\)
=>\(14⋮n-3\)
=>\(n-3\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
=>\(n\in\left\{4;2;5;1;10;-4;17;-11\right\}\)
mà n>=0
nên \(n\in\left\{4;2;5;1;10;17\right\}\)
(3n + 5) ⋮ (n - 3) đk n \(\in\) N
3(n - 3) + 14 ⋮ n - 3
14 ⋮ n - 3
n - 3 \(\in\) Ư(14) = {-14; -7; -2; -1; 1; 2; 7; 14}
n \(\in\) {-11; -4; 1; 2; 4; 5; 10; 17}
Vì n \(\in\) N nên n \(\in\) { 1; 2; 4; 5; 10; 17}

1: \(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)
\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1+x-3\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)
2: \(\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(1-3x\right)\left(1+3x\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+1\right)-\left(1-9x^2\right)\)
\(=x^3-3x^2+3x-1-x^3-1-1+9x^2\)
\(=6x^2+3x-3\)
3: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-1\right)\left(x+1\right)+3x\)
\(=x^3+8-x\left(x^2-1\right)+3x\)
\(=x^3+8-x^3+x+3x=4x+8\)
4: \(\left(3x-2\right)^2-3\left(x-4\right)\left(x+4\right)+\left(x-3\right)^2-\left(x+1\right)\left(x^2-x+1\right)\)
\(=9x^2-12x+4-3\left(x^2-16\right)+x^2-6x+9-\left(x^3+1\right)\)
\(=10x^2-18x+13-3x^2+48-x^3-1\)
\(=-x^3+7x^2-18x+12\)
5: \(\left(x+1\right)^2-\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)\)
\(=x^2+2x+1-x^2+2x-1-3\left(x^2-9\right)\)
\(=4x-3x^2+27\)
6: \(\left(x-1\right)^3-x\left(x-2\right)^2+x-1\)
\(=x^3-3x^2+3x-1-x\left(x^2-4x+4\right)+x-1\)
\(=x^3-3x^2+4x-2-x^3+4x^2-4x\)
\(=x^2-2\)
7: \(\left(x+2\right)^3-x^2\left(x+6\right)-8\)
\(=x^3+6x^2+12x+8-x^3-6x^2-8\)
=12x
8: \(\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
9: \(\left(x-1\right)^3-\left(x+1\right)^3+6\left(x-1\right)\left(x+1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)
\(=-6x^2-2+6x^2-6=-8\)
10: \(4x\left(3x-5\right)-2\left(4x+1\right)-x-7\)
\(=12x^2-20x-8x-2-x-7\)
\(=12x^2-29x-9\)
11: \(\left(3x+1\right)^2-2\left(3x+1\right)\left(5x+5\right)+\left(5x+5\right)^2\)
\(=\left(5x+5-3x-1\right)^2\)
\(=\left(2x+4\right)^2=4x^2+16x+16\)
12: \(\left(2x+3\right)^2+\left(2x+3\right)\left(2x-6\right)+\left(x-3\right)^2\)
\(=\left(2x+3\right)^2+2\cdot\left(2x+3\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+3+x-3\right)^2=\left(3x\right)^2=9x^2\)
13: \(\left(x^2-2x+4\right)\left(x+2\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3+8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x+7+3x^2-3=-3x+4\)
14: \(\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+4\left(x+1\right)^2\)
\(=\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+\left(2x+2\right)^2\)
\(=\left(x-2+2x+2\right)^2=\left(3x\right)^2=9x^2\)


 SOS cần gấp
SOS cần gấp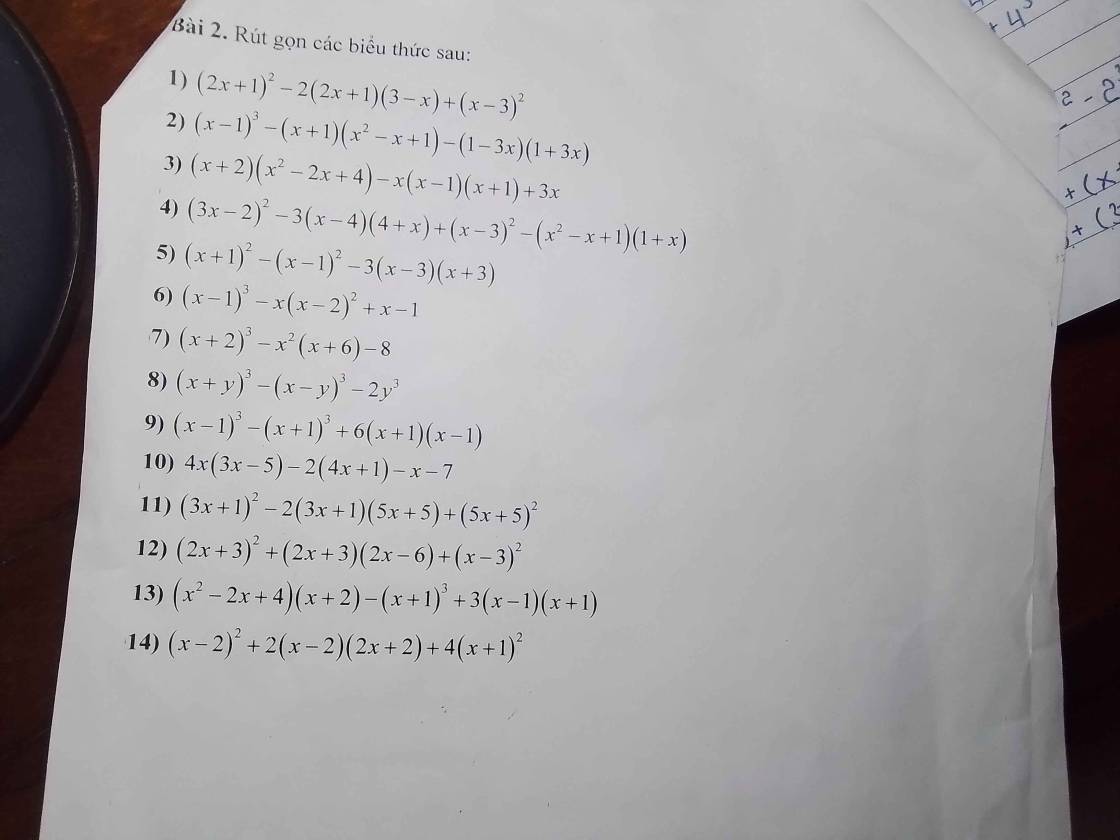
6: \(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{AB}{DC}=\dfrac{1}{2}\)
=>\(S_{ADC}=2\times S_{ABC}\)
Ta có: \(S_{ABC}+S_{ADC}=S_{ABCD}\)
=>\(3\times S_{ABC}=96\)
=>\(S_{ABC}=32\left(cm^2\right)\)
5: Số gạo bán được trong 2 ngày đầu tiên chiếm:
1-20%=80%
Tổng số gạo ban đầu là:
(125+135):80%=260:0,8=325(kg)