Câu 12:
Quy luật: Ta thấy các chữ số hàng thứ 2 sẽ tương ứng bằng các số ở hàng thứ nhất cùng cột nhân với 3

Tương tự: Các chữ số ở hàng thứ 3 sẽ bằng các số ở hàng thứ nhất cùng cột nhân với 6 (24 = 4 x 6, 18 = 3 x 6, 6 = 1 x 6)

Vậy số trong dấu ? là: 2 x 6 = 12

Đáp án C.

Các số đó là : 11; 13; 31; 17; 71; 37; 73; 79; 97.

TICK giúp mih vs 

 Quan trọng là làm sao để tìm ra được ấy chứ còn chỉ cần tìm không thì dễ rồi.

\(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + ... + \(\dfrac{2}{x:\left(x+1\right)}\) = \(\dfrac{2011}{2013}\)

\(\dfrac{1}{2}\) \(\times\) (\(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + ... + \(\dfrac{2}{x}:\left(x+1\right)\) = \(\dfrac{2011}{2013}\) \(\times\) \(\dfrac{1}{2}\)

\(\dfrac{1}{2\times3}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + ... + \(\dfrac{2}{2x\times\left(x+1\right)}\) = \(\dfrac{2011}{2013}\) \(\times\) \(\dfrac{1}{2}\)

\(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) + \(\dfrac{1}{4\times5}\) + ... + \(\dfrac{1}{x\times\left(x+1\right)}\) = \(\dfrac{2011}{2013}\) \(\times\) \(\dfrac{1}{2}\)

  \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\)  - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + ... + \(\dfrac{1}{x}\) - \(\dfrac{1}{x+1}\) = \(\dfrac{2011}{2013}\) \(\times\) \(\dfrac{1}{2}\)

  \(\dfrac{1}{2}\) - \(\dfrac{1}{x+1}\) = \(\dfrac{2011}{2013}\) \(\times\) \(\dfrac{1}{2}\)

      \(\dfrac{1}{x+1}\) = \(\dfrac{1}{2}\) - \(\dfrac{2011}{2013\times2}\) 

      \(\dfrac{1}{x+1}\)  = \(\dfrac{2013-2011}{2\times2013}\)

        \(\dfrac{1}{x+1}\) = \(\dfrac{2}{2\times2013}\)

          \(\dfrac{1}{x+1}\) = \(\dfrac{1}{2013}\)

              \(x\) + 1 = 2013 

              \(x\) = 2013 - 1

                \(x\) = 2012

Lời giải:
$\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x(x+1)}=\frac{2011}{2013}$

$\frac{2}{6}+\frac{2}{12}+\frac{2}{20}+....+\frac{2}{x(x+1)}=\frac{2011}{2013}$

$\frac{2}{2.3}+\frac{2}{3.4}+\frac{2}{4.5}+....+\frac{2}{x(x+1)}=\frac{2011}{2013}$

$2\left(\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+....+\frac{x+1-x}{x(x+1)}\right)=\frac{2011}{2013}$

$2(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{x}-\frac{1}{x+1})=\frac{2011}{2013}$

$2(\frac{1}{2}-\frac{1}{x+1})=\frac{2011}{2013}$

$\frac{1}{2}-\frac{1}{x+1}=\frac{2011}{2013}:2=\frac{2011}{4026}$

$\frac{1}{x+1}=\frac{1}{2}-\frac{2011}{4026}=\frac{1}{2013}$

$x+1=2013$

$x=2013-1$

$x=2012$

21, 20 ,18, 15 ,11, 6, 0. 

giải thích: khoảng cách giữa 21 và 20 là 1, khoảng cách giữa 20 và 18 là 2, khoảng cách giữa 18 và 15 là 3, khoảng cách giữa 15 và 11 là 4, vậy khoảng cách giữa 11 và số cần điền tiếp là 5 ( ta lấy 11 - 5 ) ,..... vv

Chỗ chấm nào thế em?

             Giải: 

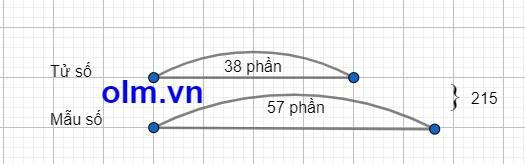
    Theo bài ra ta có sơ đồ

    Theo sơ đồ ta có: 

    Tử số của phân số là:  215 : (38 + 57) x 38 = 86

     Mẫu số của phân số là: 215 - 86 = 129 

     Phân số cần tìm là: \(\dfrac{86}{129}\) 

     Đáp số:.... 

a: Vì ABCD là hình thang

nên \(d\left(A;BC\right)=d\left(D;BC\right)=d\left(B;AD\right)=d\left(C;AD\right)\)

\(S_{ABC}=\dfrac{1}{2}\times BC\times d\left(A;BC\right)\)

\(S_{DBC}=\dfrac{1}{2}\times BC\times d\left(D;BC\right)\)

mà \(d\left(A;BC\right)=d\left(D;BC\right)\)

nên \(S_{ABC}=S_{DBC}\)

\(S_{BAD}=\dfrac{1}{2}\times AD\times d\left(B;AD\right)\)

\(S_{CAD}=\dfrac{1}{2}\times AD\times d\left(C;AD\right)\)

mà \(d\left(B;AD\right)=d\left(C;AD\right)\)

nên \(S_{BAD}=S_{CAD}\)

Vì AD//BC

nên \(\dfrac{IA}{IC}=\dfrac{ID}{IB}=\dfrac{AD}{BC}=\dfrac{1}{3}\)

=>IC=3IA;IB=3ID

Vì IC=3IA

nên \(S_{DIC}=3S_{DAI}\)

Vì IB=2ID

nên \(S_{ABI}=3S_{ADI}\)

=>\(S_{ABI}=S_{DIC}\)

b: Vì IC=3IA

nên \(S_{ICB}=3\cdot S_{IAB}=9\cdot S_{AID}\)

Ta có: \(S_{AID}+S_{DIC}+S_{AIB}+S_{BIC}=S_{ABCD}\)

=>\(\left(9+3+3+1\right)\cdot S_{AID}=48\)

=>\(S_{AID}=3\left(cm^2\right)\)

=>\(S_{AIB}=3\cdot3=9\left(cm^2\right)\)

Mình nghĩ là đáp án B bạn nhé

B

\(3200+\overline{abc}=81\times\overline{abc}\\ 81\times\overline{abc}-\overline{abc}=3200\\ 80\times\overline{abc}=3200\\ \overline{abc}=3200:80\\ \overline{abc}=40\)(Bạn xem lại đề xem có sai đề không nhỉ, \(\overline{abc}\) là số có 3 chữ số mà kết quả lại ra 40)

\(3200+\overline{abc}=81\times\overline{abc}\)

\(3200=81\times\overline{abc}-\overline{abc}\)

\(3200=81\times\overline{abc}-\overline{abc}\times1\)

\(3200=\overline{abc}\times80\)

            \(\overline{abc}=3200:80\)

            \(\overline{abc}=40\)

\(3200=\overline{abc}\times\left(81-1\right)\)

ko bt

thế còn cách kiếm

Bài 1:

a: Xét ΔAHB  và ΔAHC có

AB=AC

AH chung

HB=HC

Do đó: ΔAHB=ΔAHC

=>\(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

=>AH\(\perp\)BC

b: Xét ΔIBC có

IH là đường cao

IH là đường trung tuyến

Do đó: ΔIBC cân tại I

c: Ta có: MN//BC

=>\(\widehat{INM}=\widehat{ICB};\widehat{IMN}=\widehat{IBC}\)

mà \(\widehat{ICB}=\widehat{IBC}\)(ΔIBC cân tại I)

nên \(\widehat{INM}=\widehat{IMN}\)

=>ΔIMN cân tại I

Ta có: MN//BC

IA\(\perp\)BC

Do đó: IA\(\perp\)MN

ΔIMN cân tại I

mà IA là đường cao

nên A là trung điểm của MN

d: Xét ΔAEI vuông tại E và ΔAFI vuông tại F có

AI chung

\(\widehat{IAE}=\widehat{IAF}\)(ΔAHB=ΔAHC)

Do đó: ΔAEI=ΔAFI

=>IE=IF

Xét ΔBEI vuông tại E và ΔBHI vuông tại H có

BI chung

\(\widehat{EBI}=\widehat{HBI}\)

Do đó: ΔBEI=ΔBHI

=>IE=IH

=>IE=IF=IH

Bài 2:

a: Xét ΔFAD và ΔFCB có

FA=FC

\(\widehat{AFD}=\widehat{CFB}\)

FD=FB

Do đó: ΔFAD=ΔFCB

=>AD=CB

b: ΔFAD=ΔFCB

=>\(\widehat{FAD}=\widehat{FCB}\)

=>AD//BC

Xét ΔEAH và ΔEBC có

EA=EB

\(\widehat{AEH}=\widehat{BEC}\)(hai góc đối đỉnh)

EH=EC

Do đó: ΔEAH=ΔEBC

=>\(\widehat{EAH}=\widehat{EBC}\)

=>AH//BC

Ta có: ΔEAH=ΔEBC

=>AH=BC

mà AD=BC

nên AH=AD

Ta có: AH//BC

AD//BC

mà AH,AD có điểm chung là A

nên H,A,D thẳng hàng

mà AH=AD

nên A là trung điểm của DH

c: Xét ΔFDC và ΔFBA có

FD=FB

\(\widehat{DFC}=\widehat{BFA}\)(hai góc đối đỉnh)

FC=FA

Do đó: ΔFDC=ΔFBA

=>\(\widehat{FDC}=\widehat{FBA}\)

=>DC//BA

d: Gọi giao điểm của CE và BF là K

Xét ΔABC có

BF,CE là các đường trung tuyến

BF cắt CE tại K

Do đó: K là trọng tâm của ΔABC

=>AK đi qua trung điểm M của BC

Ta có: DC//BA

=>CP//AB

Xét tứ giác ACBH có

AH//BC

AH=BC

Do đó: ACBH là hình bình hành

=>BH//AC

=>BP//AC

Xét tứ giác ABPC có

AB//PC

AC//BP

Do đó: ABPC là hình bình hành

=>AP cắt BC tại trung điểm của mỗi đường

mà M là trung điểm của BC

nên M là trung điểm của AP

=>A,M,P thẳng hàng

=>A,K,P thẳng hàng

=>AP,CH,BD đồng quy