Cho x,y,z là các số thỏa mãn x+y+z = 0. Chứng minh rằng Biểu thức 2023xy + 2024 yz +4047zx Không thể nhận giá dương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(=(\frac{-5}{12}+\frac{17}{12})+(\frac{4}{37}+\frac{-41}{37})=\frac{12}{12}+\frac{-37}{37}=1+(-1)=0\)
b.
\(=\frac{-20}{24}+\frac{9}{24}-\frac{1}{10}=\frac{-11}{24}+\frac{1}{10}=\frac{-43}{120}\)
c.
\(=\frac{-25}{27}-\frac{31}{42}+\frac{7}{27}+\frac{3}{42}\\ =\frac{-25}{27}+\frac{7}{27}+(\frac{-31}{42}+\frac{3}{42})\\ =\frac{-2}{3}+\frac{-2}{3}=\frac{-4}{3}\)
d.
\(=\frac{5}{36}+\frac{-28}{36}-\frac{5}{4}=\frac{5}{36}+\frac{-28}{36}-\frac{45}{36}\\ =\frac{-68}{36}=\frac{-17}{9}\)
e.
\(=\frac{3}{5}+\frac{2}{5}: 2=\frac{3}{5}+\frac{1}{5}=\frac{4}{5}\)
f.
\(=\frac{3}{10}(\frac{-23}{7}+\frac{13}{7})=\frac{3}{10}.\frac{-10}{7}=\frac{-3}{7}\)
g.
\(=\frac{3}{2}+\frac{1}{4}+(-1)=\frac{7}{4}-1=\frac{3}{4}\)
h.
\(=\frac{2^{2023}}{(2^2)^{1011}}=\frac{2^{2023}}{2^{2022}}=2^{2023-2022}=2\)
i.
\(=4-4+(-8).\frac{5}{4}=0+(-10)=-10\)

Bà ngoại là người mà tôi cảm thấy yêu thương và kính trọng nhất. Năm nay, bà sáu mươi lăm tuổi. Khi còn nhỏ, bố mẹ em thường xuyên bận công việc. Bà là người chăm sóc tôi . Những kỉ niệm với bà thật đẹp. Tôi vẫn nhớ những lúc nằm ngủ cạnh bà, nghe bà kể chuyện. Giọng kể của bà thật hấp dẫn. Những câu chuyện cổ tích mà bà kể đến bây giờ tôi vẫn còn nhớ. Không chỉ vậy, bà còn dạy cho tôi rất nhiều bài học bổ ích. Nhờ có bà mà tôi đã biết yêu thương và kính trọng mọi người xung quanh. Tôi cũng đã tự giác hơn trong công việc và học tập. Tôi rất yêu thương người bà của mình. Từ tận đáy lòng, tôi luôn tự nhủ sẽ cố gắng học tập thật tốt để bà luôn tự hào về cháu gái của mình.

Để A có giá trị là một số nguyên thì:
\(\left(\sqrt{x}+1\right)⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)+4⋮\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow4⋮\left(\sqrt{x}-3\right)\)
Vì \(x\in Z\) nên \(\left(\sqrt{x}-3\right)\inƯ\left(4\right)=\left\{\pm1,\pm2,\pm4\right\}\)
Ta có bảng sau:
| \(\sqrt{x}-3\) | 1 | -1 | 2 | -2 | 4 | -4 |
| \(\sqrt{x}\) | 4 | 2 | 5 | 1 | 7 | -1 |
| x | 16 | 4 | 25 | 1 | 49 | (loại) |
Vậy ....
Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\left(\sqrt{x}-3\right)+4}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}-3}=\dfrac{4}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)
Để A có giá trị là một số nguyên khi:
\(4⋮\sqrt{x}-3\) hay \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Do đó:
\(\sqrt{x}-3=-1\Rightarrow\sqrt{x}=-1+3=2\Rightarrow x=4\)
\(\sqrt{x}-3=1\Rightarrow\sqrt{x}=1+3=4\Rightarrow x=16\)
\(\sqrt{x}-3=-2\Rightarrow\sqrt{x}=-2+3=1\Rightarrow x=1\)
\(\sqrt{x}-3=2\Rightarrow\sqrt{x}=2+3=5\Rightarrow x=25\)
\(\sqrt{x}-3=-4\Rightarrow\sqrt{x}=-4+3=-1\) ( loại )
\(\sqrt{x}-3=4\Rightarrow\sqrt{x}=4+3=7\Rightarrow x=49\)
Vậy để A là một số nguyên khi \(x\in\left\{4;16;1;25;49\right\}\)

camera của một thiết bị bắn tốc độ ghi hình và tính được thời gian một ô tô chạy qua giữa hai vạch mốc cách nhau 20m là không phải 8s nếu tốc độ giới hạn quy định trên đoạn đường đó là tám mươi kilômét trên giờ thì ô tô này có vượt quá tốc độ cho phép hay không
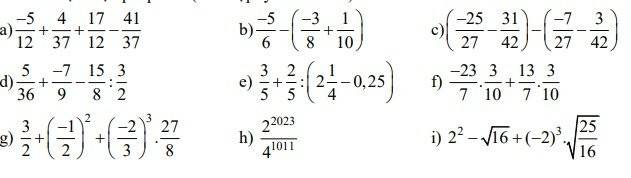
Lời giải:
$2023xy+2024yz+4047xz=2023xy+2024y(-x-y)+4047x(-x-y)$
$=-2024y^2-4047x^2-4048xy$
$=-[4047x^2+2024y^2+4048xy]$
$=-[2024(x^2+y^2+2xy)+2023x^2]=-[2024(x+y)^2+2023x^2]$
Vì $2024(x+y)^2+2023x^2\geq 0$ với mọi $x,y$
$\Rightarrow -[2024(x+y)^2+2023x^2]\leq 0$ với mọi $x,y$
Do đó nó không thể nhận giá trị dương.