Lời giải:

$A=(4a^2+4b^2+c^2+8ab-4ac-4bc)+(4b^2+4c^2+a^2+8bc-4ab-4ac)+(4c^2+4a^2+b^2+8ac-4bc-4ab)$

$=6(a^2+b^2+c^2)=6m$

\(\dfrac{7^{49}-7^{48}}{7^{48}}\)

\(=\dfrac{7^{49}}{7^{48}}-\dfrac{7^{48}}{7^{48}}\)

\(=7-1\)

\(=6\)

\(\dfrac{7^{49}-7^{48}}{7^{48}}\)

\(=\dfrac{7^{48}\cdot7-7^{48}}{7^{48}}\)

\(=\dfrac{7^{48}\left(7-1\right)}{7^{48}}\)

\(=7-1\)

\(=6\)

13) 

a) \(\left\{{}\begin{matrix}7x+4y=2\\5x-2y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x+4y=2\\10x-4y=32\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}7x+4y=2\\17x=34\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\cdot2+4y=2\\x=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4y=2-14\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4y=-12\\x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)

Vậy: .... 

b) \(\left\{{}\begin{matrix}2x+3y=19\\3x+4y=-14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=57\\6x+8y=-28\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=19\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot85=19\\y=85\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=19-255\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-236\\y=85\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-118\\y=85\end{matrix}\right.\)

Vậy: .... 

c) \(\left\{{}\begin{matrix}2x+2y=3\\3x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x=5\\3x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\3\cdot1-2y=2\end{matrix}\right.\)

 \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\-2y=2-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\-2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{2}\end{matrix}\right.\)

Vậy: ....

15) 

a) \(\left\{{}\begin{matrix}5\left(x+2\right)=2\left(y+7\right)\\3\left(x+y\right)=17-x\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x+10=2y+14\\3x+3y=17-x\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=14-10\\3x+3y+x=17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=4\\4x+3y=17\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}15x-6y=12\\8x+6y=34\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=4\\23x=46\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5\cdot2-2y=4\\x=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2y=6\\x=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=2\end{matrix}\right.\)

vậy: ... 

Gọi giá tiền mỗi kg gạo mà bác Lan đã mua là \(x\) (nghìn đồng; \(x>2\))

Số gạo bác Lan đã mua là: \(\dfrac{480}{x}\) (kg)

Giá tiền mỗi kg gạo theo dự định là: \(x-2\) (nghìn đồng)

Số gạo bác Lan dự định mua là: \(\dfrac{480}{x-2}\) (kg)

Vì bác Lan đã mua lượng gạo giảm \(\dfrac{1}{16}\) lần so với dự định nên ta có phương trình:

\(\dfrac{480}{x-2}.\left(1-\dfrac{1}{16}\right)=\dfrac{480}{x}\)

\(\Leftrightarrow\dfrac{15}{16\left(x-2\right)}=\dfrac{1}{x}\)

\(\Rightarrow15x=16x-32\)

\(\Leftrightarrow x=32\left(tm\right)\)

Vậy giá tiền mỗi kg gạo mà bác Lan đã mua là 32000 đồng.

\(3x^3-14x^2+4x+3\)

\(=3x^3+x^2-15x^2-5x+9x+3\)

\(=x^2\left(3x+1\right)-5x\left(3x+1\right)+3\left(3x+1\right)\)

\(=\left(3x+1\right)\left(x^2-5x+3\right)\)

\(\dfrac{4x^2+16}{x^2+6}=\dfrac{3}{x^2+1}+\dfrac{5}{x^2+3}+\dfrac{7}{x^2+5}\)

=>\(\dfrac{4x^2+16}{x^2+6}-3=\dfrac{3}{x^2+1}-1+\dfrac{5}{x^2+3}-1+\dfrac{7}{x^2+5}-1\)

=>\(\dfrac{x^2-2}{x^2+6}=\dfrac{-x^2+2}{x^2+1}+\dfrac{-x^2+2}{x^2+3}+\dfrac{-x^2+2}{x^2+5}\)

=>\(\dfrac{x^2-2}{x^2+6}+\dfrac{x^2-2}{x^2+1}+\dfrac{x^2-2}{x^2+3}+\dfrac{x^2-2}{x^2+5}=0\)

=>\(\left(x^2-2\right)\left(\dfrac{1}{x^2+6}+\dfrac{1}{x^2+1}+\dfrac{1}{x^2+3}+\dfrac{1}{x^2+5}\right)=0\)

=>\(x^2-2=0\)

=>\(x^2=2\)

=>\(x=\pm\sqrt{2}\)

Gọi vận tốc của ca nô khi nước yên lặng là: x (km/h) 

ĐK: x>3

Vận tốc của ca nô khi đi xuôi dòng là: x + 3 (km/h) 

Thời gian ca nô đi xuôi dòng là: `24/(x+3)` (km/h) 

Vận tốc của ca nô khi đi ngược dòng là: x - 3 (km/h)

Thời gian ca nô đi ngược dòng là: `24/(x-3)`  

Thời gian đi xuôi dòng lớn hơn thời gian đi ngược dòng 40 phút nên ta có pt:

\(\dfrac{24}{x-3}-\dfrac{24}{x+3}=\dfrac{40}{60}\)

\(\Leftrightarrow\dfrac{24\left(x+3\right)-24\left(x-3\right)}{x^2-9}=\dfrac{2}{3}\)

\(\Leftrightarrow\dfrac{144}{x^2-9}=\dfrac{2}{3}\)

\(\Leftrightarrow x^2-9=144:\dfrac{2}{3}\)

\(\Leftrightarrow x^2-9=216\)

\(\Leftrightarrow x^2=225\)

\(\Leftrightarrow\left[{}\begin{matrix}x=15\left(tm\right)\\x=-15\left(ktm\right)\end{matrix}\right.\)

Vậy: ...

Gọi tốc độ của dòng nước là x (km/h) (0 < x < 27).

Khi đó, tốc độ của ca nô khi đi xuôi dòng là 27 + x (km/h) và tốc độ của ca nô khi đi ngược dòng là 27 – x (km/h).

Thời gian ca nô đi xuôi dòng quãng đường AB là $\frac{40}{27+x}$ (giờ).

Thời gian ca nô đi ngược dòng quãng đường AB là $\frac{40}{27-x}$ (giờ).

Theo bài, thời gian cả đi và về là 3 giờ nên ta có phương trình: $\frac{40}{27+x}+\frac{40}{27-x}=3.$

Giải phương trình: $\frac{40}{27+x}+\frac{40}{27-x}=3.$

$\frac{40\left(27-x\right)}{\left(27+x\right)\left(27-x\right)}+\frac{40\left(27+x\right)}{\left(27+x\right)\left(27-x\right)}=\frac{3\left(27+x\right)\left(27-x\right)}{\left(27+x\right)\left(27-x\right)}$

                     40(27 – x) + 40(27 + x) = 3(27 + x)(27 – x)

                 1 080 – 40x + 1 080 + 40x = 3(729 – x2)

                 1 080 – 40x + 1 080 + 40x = 2 187 – 3x2

1 080 – 40x + 1 080 + 40x – 2 187 + 3x2 = 0

                                                    3x2 – 27 = 0

                                                        x2 – 9 = 0

                                            (x – 3)(x + 3) = 0

                                             x – 3 = 0 hoặc x + 3 = 0

                                                   x = 3 hoặc x = –3.

Do 0 < x < 27 nên x = 3.

Vậy tốc độ của dòng nước là 3 km/h.

Bài 3:

Gọi tốc độ ban đầu của ô tô là: x (km/h) 

ĐK: x > 0 

Thời gian ô tô đi trên quãng đường 30km đầu là: \(\dfrac{30}{x}\left(h\right)\) 

Vẫn tốc của ô tô khi đi trên quãng đường 31,5km còn lại là: `x+2` (km/h) 

Thời gian ô tô đi trên quãng đường 31,5km còn lại là: \(\dfrac{31,5}{x+2}\left(h\right)\)

Mà thời gian đi trên hai quãng đường này bằng nhau nên ta có pt:

\(\dfrac{30}{x}=\dfrac{31,5}{x+2}\)

\(\Leftrightarrow30\left(x+2\right)=31,5x\)

\(\Leftrightarrow30x+60=31,5x\)

\(\Leftrightarrow31,5x-30x=60\)

\(\Leftrightarrow1,5x=60\)

\(\Leftrightarrow x=\dfrac{60}{1,5}\)

\(\Leftrightarrow x=40\left(tm\right)\)

Vậy: ... 

Bài 3

Gọi x (km/h) là tốc độ ban đầu của ô tô (x > 0)

Tốc độ lúc sau là: x + 2 (km/h)

Thời gian đi 30 km:

  Thời gian ô tô đi quãng đường 31,5 km:

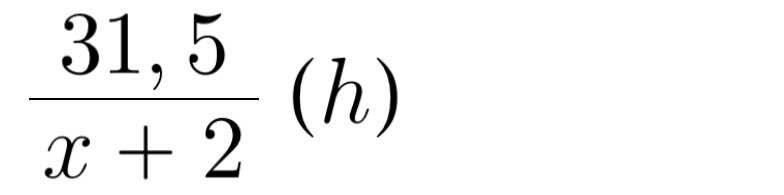  Theo đề bài ta có phương trình:

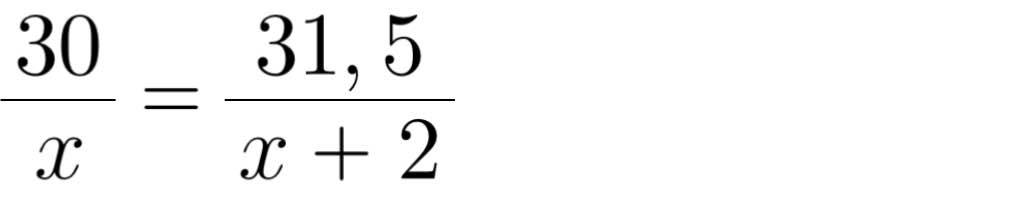 30(x + 2) = 31,5x

30x + 60 = 31,5x

31,5x - 30x = 60

1,5x = 60

x = 60 : 1,5

x = 40 (nhận)

Vậy tốc độ lúc đầu của ô tô là 40 km/h