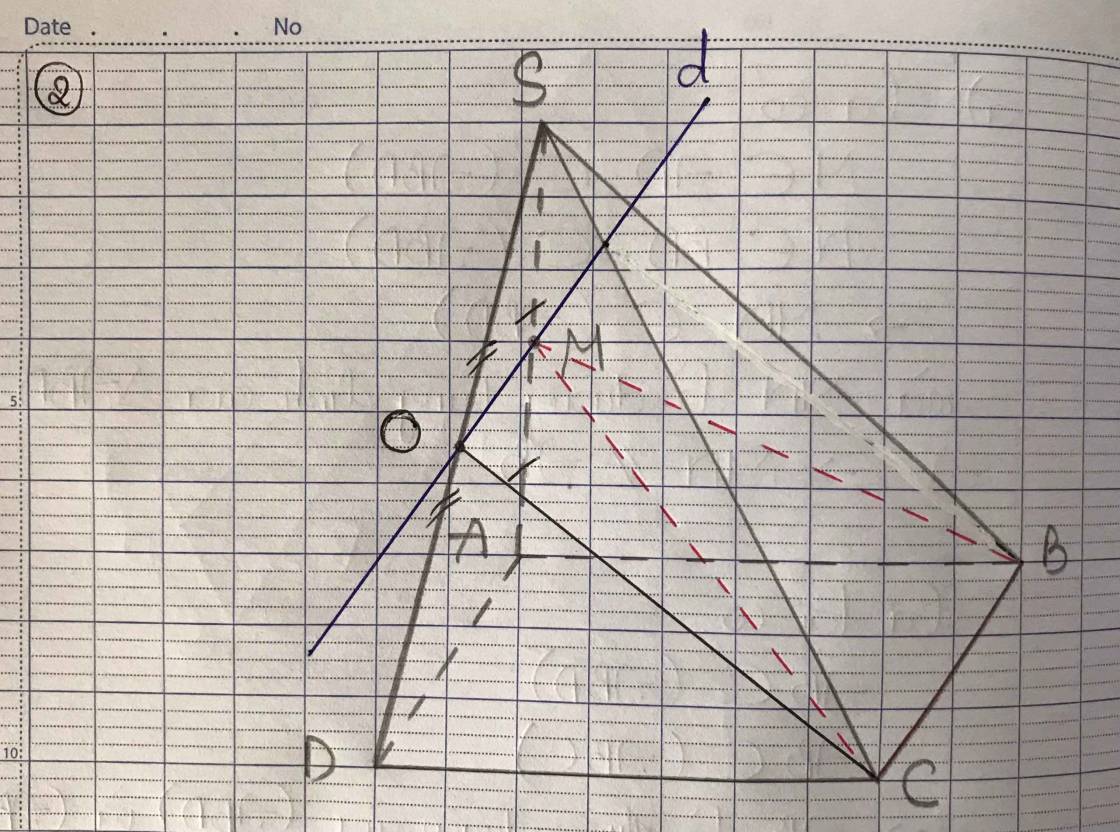
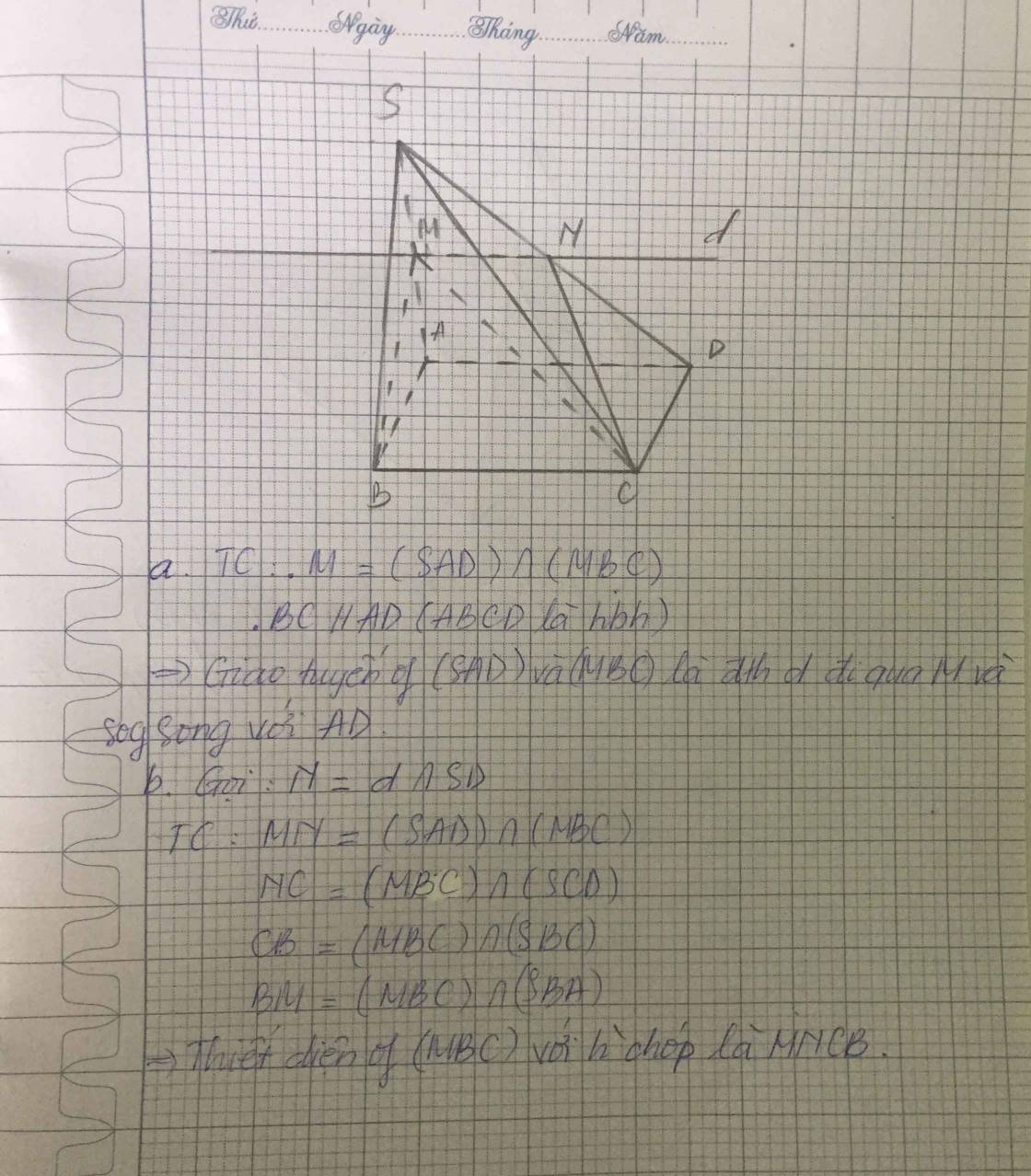
a) Gọi H là trung điểm của SC

Ta có:

DGDH=23(1)DGDH=23(1) 

BC∥AD⇒ODOB=OAOC=ADBC=2BC∥AD⇒ODOB=OAOC=ADBC=2 

⇒OD=2OB⇒OD=2OB 

⇒ODBD=23(2)⇒ODBD=23(2)

Từ (1) và (2) ⇒DGDH=ODBD⇒OG∥BH⇒DGDH=ODBD⇒OG∥BH

BH⊂(SBC)⇒OG∥(SBC)BH⊂(SBC)⇒OG∥(SBC)

b) Gọi M’ là trung điểm của SA⇒MM′∥ADSA⇒MM′∥AD và MM′=AD2MM′=AD2. Mặt khác vì BC∥ADBC∥AD và BC=AD2BC=AD2 nên BC∥MM′BC∥MM′ và BC=MM′BC=MM′.

Do đó tứ giác BCMM’ là hình bình hành ⇒CM∥BM′⇒CM∥BM′ mà BM′⊂(SAB)BM′⊂(SAB)

⇒CM∥(SAB)⇒CM∥(SAB) 

c) Ta có: OCOA=12OCOA=12 nên OCCA=13OCCA=13. Mặt khác vì SC=32SISC=32SI nên CICS=13CICS=13.

OCCA=CICS⇒OI∥SAOCCA=CICS⇒OI∥SA

OI⊂(BID)⇒SA∥(BID)

Hai tam giác CBA và DBA là hai tam giác đều cạnh a

=> ∆ CBA = ∆ DBA ( c.c.c)

=> CM = DM ( 2 đường trung tuyến tương ứng)

=> Tam giác CMD cân tại M.

Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD

* Chứng minh tương tự, ta có: MN ⊥ AB

Do đó, MN là đoạn vuông góc chung của AB và CD.

* Tam giác BCD là tam giác đều cạnh a nên

\(BN=\sqrt{BC^2-CN^2}=\frac{a\sqrt{3}}{2}\)

Bài này học rồi mà bà

1 + 1 mà là toán lớp 11 à?

ừ đúng rồi

2 nha 

k cho mình

hok tốt 

2

Bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb