1 nêu mối quan hệ giữa trồng trọt và chăn nuôi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Những tia nắng mặt trời mềm mại làm bóng mình những tán lá xanh tươi của cây bàng. Trên cành cây, lá rợp như một tấm thảm màu xanh mát, tô điểm cho không gian trời rộng lớn. Khi tiếng chuông báo động chào cờ vang lên, tôi cảm nhận sự hồi hộp và phấn khích lan tỏa trong không khí.
Nhìn xung quanh, tôi thấy đám học sinh sôi nổi, mặc bộ đồng phục trắng xóa. Bước chân vỗ nhẹ trên lớp cỏ mềm mại, tôi là một phần của cảnh sắc sống động, chứng kiến sự tụ tập của hàng trăm tâm hồn trẻ thơ. Ánh mắt họ tỏa sáng như những ánh sao, tràn đầy năng lượng tích cực.
Khi lá cờ đỏ tung bay, bóng mình cây bàng rung động như một điệu nhảy nhẹ, là sự chào đón ngày mới đầy hứng khởi. Tôi, cây bàng, là một nhân chứng yên bình và vững chắc cho những khoảnh khắc trọng đại trên sân trường, nơi hồn trường học tỏa sáng giữa vẻ đẹp tự nhiên và sự tương tác của con người.

M N A B C E F
a/ Xét tg AEM và tg BCM có
MA=MB (gt); ME=MC (gt)
\(\widehat{AME}=\widehat{BMC}\) (góc đối đỉnh)
=> tg AEM = tg BCM (c.g.c)
b/
Ta có
NA=NC(gt); NF=NB(gt)
\(\Rightarrow\dfrac{NA}{NC}=\dfrac{NF}{NB}=1\) => AF//BC (Talet đảo)
c/
C/m tương tự như câu b ta cũng có AE//BC
=> A; E; F thẳng hàng (Từ 1 điểm ngoài 1 đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
Ta có
AE//BC (cmt)
MA=MB (gt)
\(\Rightarrow\dfrac{AE}{BC}=\dfrac{MA}{MB}=1\)
Ta có
AF//BC (cmt)
\(\Rightarrow\dfrac{AF}{BC}=\dfrac{NA}{NC}=1\)
\(\Rightarrow\dfrac{AE}{BC}=\dfrac{AF}{BC}\Rightarrow AE=AF\)

\(x\left(x-y\right)=\dfrac{3}{10}\Rightarrow x-y=\dfrac{3}{10x}\left(1\right)\)
\(y\left(x-y\right)=\dfrac{-3}{50}\Rightarrow x-y=\dfrac{-3}{50y}\left(2\right)\)
Từ (1) và (2) ta có:
\(\dfrac{3}{10x}=\dfrac{-3}{50y}\)
\(\Rightarrow10x=-50y\)
\(\Rightarrow x=-\dfrac{50y}{10}=-5y\)
Thay x = -5y vào (1) ta có:
\(-5y-y=\dfrac{3}{10\cdot-5y}\)
\(\Rightarrow-6y=\dfrac{3}{-50y}\)
\(\Rightarrow300y^2=3\)
\(\Rightarrow y^2=\dfrac{1}{100}\)
\(\Rightarrow y=\pm\dfrac{1}{10}\)
Khi \(y=\dfrac{1}{10}\Rightarrow x=-5\cdot\dfrac{1}{10}=-\dfrac{1}{2}\)
Khi \(y=-\dfrac{1}{10}\Rightarrow x=-5\cdot-\dfrac{1}{10}=\dfrac{1}{2}\)

\(a^2=bc\)
=>\(\dfrac{a}{b}=\dfrac{c}{a}\)
=>\(\dfrac{a}{c}=\dfrac{b}{a}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{a}=\dfrac{a+b}{a+c}=\dfrac{a-b}{c-a}\)
=>\(\dfrac{a+b}{a+c}=\dfrac{a-b}{c-a}\)
=>\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)

Truyện ngụ ngôn Kiến và châu chấu có cốt truyện rất đơn giản nhưng lại để lại ấn tượng sâu sắc trong lòng người đọc, đặc biệt là nhân vật Kiến trong truyện. Mùa hè sôi động đến, khắp nơi đều nhộn nhịp, châu chấu thì ngày đêm ca hát, vui chơi, còn Kiến thì vẫn chăm chỉ lao động, kiếm thức ăn dự trữ cho mùa đông sắp tới. Dù châu chấu có rủ chơi cùng, rồi dè bỉu Kiến lo xa, Kiến vẫn bỏ ngoài tai và tiếp tục công việc của mình. Qua đó, chúng ta có thể thấy Kiến không chỉ chăm chỉ mà còn rất có chính kiến, quyết tâm đạt được mục tiêu của mình. Mùa hè trôi qua rất nhanh và mùa đông giá rét lại về, nhờ có thức ăn dự trữ từ mùa hè cật lực lao động, mà Kiến được ở trong tổ ấm áp và đủ thức ăn để sống, còn châu chấu ta thì gần như chết vì lạnh và đói. Kiến đúng là người biết lo xa, biết chuẩn bị kĩ lường cho mọi tình huống. Đây là một ưu điểm rất đáng quý mà chúng ta phải học hỏi. Qua nhân vật Kiến, độc giả chúng ta đã học được thật nhiều bài học quý giá, có thể áp dụng ngay vào thực tiễn cuộc sống.
Tham khảo ạ.

Áp dụng tỉ lệ thức: `a/(3b)=b/(3c)=c/(3d)=d/(3a)=(a+b+c+d)/(3a+3b+3c+3d)=1/3`.
`a/(3b)=1/3 <=> a=b`
Tương tự ta có `b=c, c=d => a=b=c=d.`

a) Ta chia các tam giác này ra làm 2 loại:
Loại 1: Tam giác có 2 đỉnh là 2 trong số \(m\) điểm thẳng hàng đã cho.
Khi đó, số cách chọn điểm thứ nhất (trong số \(m\) điểm thẳng hàng là \(m\) cách; số cách chọn điểm thứ hai là \(m-1\) cách; số cách chọn điểm cuối cùng nằm ngoài đường thẳng chứa \(m\) điểm thẳng hàng là \(n-m\) cách.
Do đó số tam giác loại 1 là \(m\left(m-1\right)\left(n-m\right)\)
Loại 2: Tam giác có cả 3 đỉnh là 3 điểm nằm ngoài đường thẳng chứa \(m\) điểm thẳng hàng.
Số cách chọn điểm thứ nhất là \(n-m\) cách; số cách chọn điểm thứ hai là \(n-m-1\) cách; số cách chọn ra điểm thứ ba là \(n-m-2\) cách. Suy ra có \(\left(n-m\right)\left(n-m-1\right)\left(n-m-2\right)\) tam giác loại 2. Nhưng do tam giác tính theo cách này sẽ lặp lại 6 lần nên số tam giác loại 2 phân biệt là \(\dfrac{\left(n-m\right)\left(n-m-1\right)\left(n-m-2\right)}{6}\)
Vậy có tất cả \(m\left(m-1\right)\left(n-m\right)+\dfrac{\left(n-m\right)\left(n-m-1\right)\left(n-m-2\right)}{6}\) tam giác.
b) Số tam giác tương đương với số cách chọn ra 3 điểm trong số \(n\) điểm đã cho.
Số cách chọn ra điểm đầu tiên là \(n\) cách.
Số cách chọn ra điểm thứ hai là \(n-1\) cách.
Số cách chọn ra điểm thứ ba là \(n-2\) cách.
Suy ra có \(n\left(n-1\right)\left(n-2\right)\) tam giác. Nhưng vì mỗi tam giác đếm theo cách này sẽ lặp lại 6 lần nên số tam giác phân biệt là \(\dfrac{n\left(n-1\right)\left(n-2\right)}{6}\) .


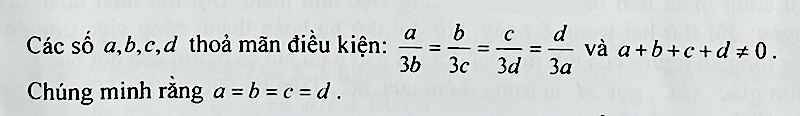
cho mượn acc bloxfruit