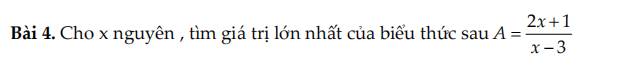`A=\frac{2x+1}{x-3}=\frac{2(x-3)+7}{x-3}=2+\frac{7}{x-3};(x\ne3)`

Để A lớn nhất thì `\frac{7}{x-3}` lớn nhất

`\Rightarrow x-3` nhỏ nhất

Mà x nguyên nên `x-3=1\Rightarrow x=4\text{ }(tm)`

Thay `x=4` vào A, ta được: 

`A=2+\frac{7}{4-3}=2+7=9`

Vậy `A_{max}=9` tại `x=4`.

\(3\left(x-2\right)=-100+211\\ 3\left(x-2\right)=111\\ x-2=37\\ x=39.\)

`#3107.101107`

`3(x - 2) = -100 + 211`

`\Rightarrow 3(x - 2) = 111`

`\Rightarrow x - 2 = 111 \div 3`

`\Rightarrow x - 2 = 37`

`\Rightarrow x = 37 + 2`

`\Rightarrow x = 39`

Vậy, `x = 39.`

Vì 120⁰ >  90⁰

Vậy góc có số đó 112⁰ là góc tù. 

112 độ lớn hơn 90 đọ -> góc tù

gọi tuổi cô giáo là x

tuổi trung bình 20HS là y

theo đề ta có: \(y=\dfrac{x}{2}\) (1)

tuổi trung bfinh của 20HS và cô giáo mà nhỏ hơn cô giáo 20 tuổi là:

\(\dfrac{20y+x}{21}=x-20\) (2)

từ (1) (2) => 

\(\dfrac{20\cdot\dfrac{x}{2}+x}{21}=x-20\\ \dfrac{10x+x}{21}=x-20\\ \dfrac{11x}{21}=x-20\\ 11x=21x-420\\ 420=21x-11x\\ 420=10x\\ x=42\)

vậy số tuổi cô giáo là 42 tuổi

\(y:84=\dfrac{106}{84}\\ y=\dfrac{106}{84}\times84\\ y=106.\)

thanks

số lần tiêu thụ pin là:

80 : 4 = 20 lần

tổng thời lượng pin tiêu thụ là:

\(20\cdot\dfrac{1}{100}=\dfrac{1}{5}\)

sau khi đi hết 80km thì lượng pin còn lại là:

\(\dfrac{1}{5}+\dfrac{2}{5}-\dfrac{1}{5}=\dfrac{2}{5}\)

vậy pin còn lại là 2/5 sau khi đi 80km

4

Đổi: 550 dag = 5500 g 

       45 hg = 4500 g
4 quả dưa cân nặng là:

5000 x 4 = 20000 ( g )

6 quả dưa cân nặng số kg là:

5500 + 4500 + 20000 = 30000 ( g ) = 30 ( kg )

Đ/s: 30 kg

làm bài giải giúp mình với

`-2/3x + 4x - 6/7 = 9/21`

`(-2/3 + 4)x - 6/7 = 9/21`

`(-2/3 + 4)x            = 9/21 + 6/7`

`(-2/3  + 4)x           = 3/7 + 6/7`

`(-2/3 + 4)x            = 9/7`

`10/3x                     = 9/7`

`          x                     = 9/7 ÷ 10/3`

`           x                     = 27/70`

`1/2x + 3/5x - 1/3x = -23/25`

`(1/2 + 3/5 - 1/3) x = -23/25`

`23/30.                    x = -23/25`

`                                 x = -23/25 ÷ 23/30`

`                                 x  = -6/5`

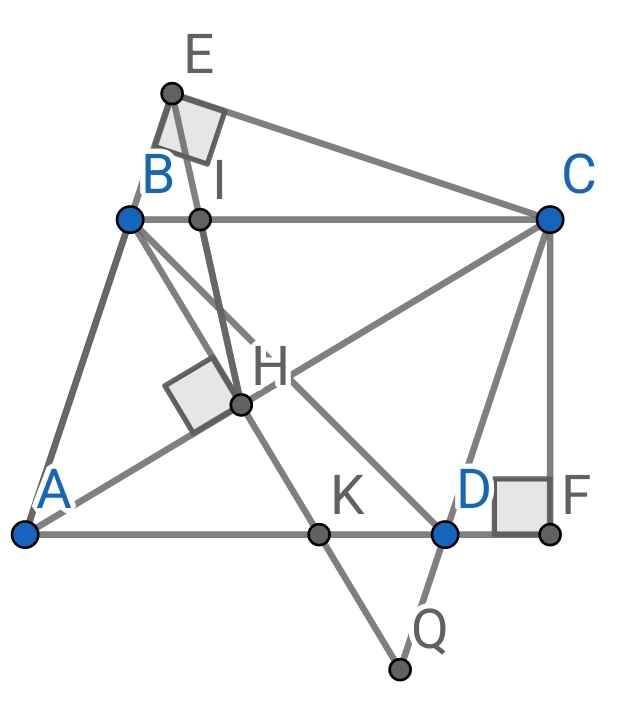
1) Xét hai tam giác vuông: ∆ABH và ∆ACE có:

∠A chung

∆ABH ∽ ∆ACE (g-g)

 ⇒ AB.AE = AH.AC

b) Sửa đề: ∆IBE ∽ ∆ICH

∆ACE vuông tại E

⇒ ∠BCE + ∠BCA = 90⁰

⇒ ∠BCE + ∠ICH = 90⁰

∆BCE vuông tại E

⇒ ∠BCE + ∠CBE = 90⁰

⇒ ∠BCE + ∠IBE = 90⁰

Mà ∠BCE + ∠ICH = 90⁰ (cmt)

⇒ ∠IBE = ∠ICH

Xét ∆IBE và ∆ICH có:

∠BIE = ∠CIH (đối đỉnh)

∠IBE = ∠ICH (cmt)

⇒ ∆IBE ∽ ∆ICH (g-g)

c) Do ABCD là hình bình hành (gt)

⇒ AB // CD và AD // BC

⇒ AB // CQ

Theo hệ quả của định lý Thales

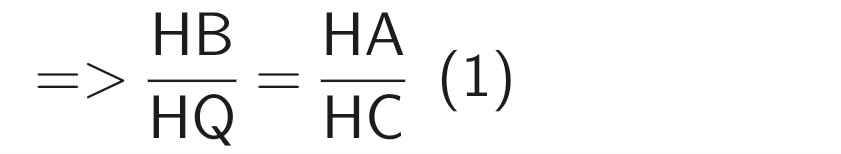
Do AD // BC (cmt)

⇒ AK // BC

Theo hệ quả của định lý Thales

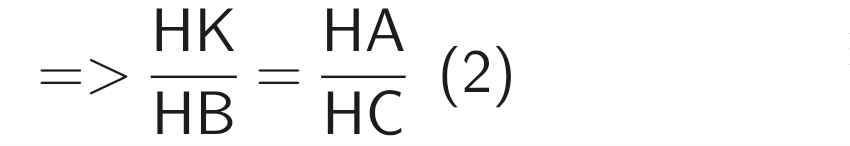 Từ (1) và (2)

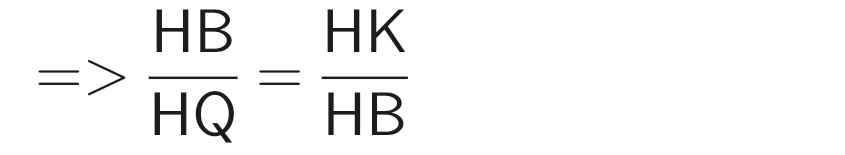 ⇒ HB.HB = HK.HQ

Hay BH.BH = HK.HQ

Lời giải:

$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0$

$\Rightarrow \frac{ab+bc+ac}{abc}=0$

$\Rightarrow ab+bc+ac=0$

Đặt $ab=x, bc=y, ca=z$ thì $x+y+z=0$

$\Rightarrow x+y=-z$.

Khi đó:

$A=\frac{b^3c^3+c^3a^3+a^3c^3}{(abc)^2}=\frac{x^3+y^3+z^3}{xyz}$

$=\frac{(x+y)^3-3xy(x+y)+z^3}{xyz}$

$=\frac{(-z)^3-3xy(-z)+z^3}{xyz}=\frac{-z^3+3xyz+z^3}{xyz}=\frac{3xyz}{xyz}=3$