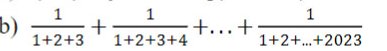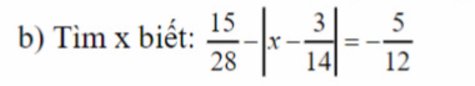Cho ABC cân tại A có BE và CF là các đường cao Gọi H là giao điểm của BE và CF . Chứng minh BE+BF>BH+CH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tuỳ theo cách vẽ bạn ạ! Nhưng bạn có thể chỉ ra các góc đối đỉnh

Bạn nên viết lại đề rõ ràng hơn. Viết thế này đọc khá khó hiểu.

a.d = b.c ⇒ \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}\) = \(\dfrac{3a}{3c}=\dfrac{2b}{2d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{2a+5b}{2c+5d}\) (1)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{3a}{3c}=\dfrac{2b}{2d}=\dfrac{3a-2b}{2c-2d}\) (2)
Từ (1) và(2) ta có:
\(\dfrac{2a+5b}{2c+5d}\) = \(\dfrac{3a-2b}{3c-2d}\)(đpcm)
a.d = b.c ⇒ \(\dfrac{a}{c}=\dfrac{b}{d}\) ⇒ \(\dfrac{a.b}{c.d}\) = \(\dfrac{a^2}{c^2}\) = \(\dfrac{b^2}{d^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a.b}{c.d}=\dfrac{a^2}{c^2}\) = \(\dfrac{b^2}{d^2}\) = \(\dfrac{a^2+b^2}{c^2+d^2}\) (đpcm)

Lời giải:
$A=\frac{1}{\frac{3.4}{2}}+\frac{1}{\frac{4.5}{2}}+....+\frac{1}{\frac{2023.2024}{2}}$
$=2(\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{2023.2024})$
$=2(\frac{4-3}{3.4}+\frac{5-4}{4.5}+....+\frac{2024-2023}{2023.2024})$
$=2(\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{2023}-\frac{1}{2024})$
$=2(\frac{1}{3}-\frac{1}{2024})=\frac{2021}{3036}$

`@` `\text {Ans}`
`\downarrow`
`b)`
`15/28 - |x-3/14| = -5/12`
`=> |x-3/14| = 15/28 - (-5/12)`
`=> |x-3/14| = 15/28 + 5/12`
`=> |x-3/14| =20/21`
`=>`\(\left[{}\begin{matrix}x-\dfrac{3}{14}=\dfrac{20}{21}\\x-\dfrac{3}{14}=-\dfrac{20}{21}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{20}{21}+\dfrac{3}{14}\\x=-\dfrac{20}{21}+\dfrac{3}{14}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{7}{6}\\x=-\dfrac{31}{42}\end{matrix}\right.\)
Vậy, `x \in {7/6; -31/42}`

\(\left(2x-1\right)^3=\dfrac{8}{27}\)
\(\Rightarrow\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
\(\Rightarrow2x-1=\dfrac{2}{3}\)
\(\Rightarrow2x=\dfrac{2}{3}+1\)
\(\Rightarrow2x=\dfrac{5}{3}\)
\(\Rightarrow x=\dfrac{5}{3}:2=\dfrac{5}{6}\)