Gọi H là trực tâm của tam giác nhọn ABC. Chứng minh rằng:
a) HA + HB + HC < AB + AC
b) HA + HB + HC < \(\dfrac{2}{3}\) (AB + BC + CA)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

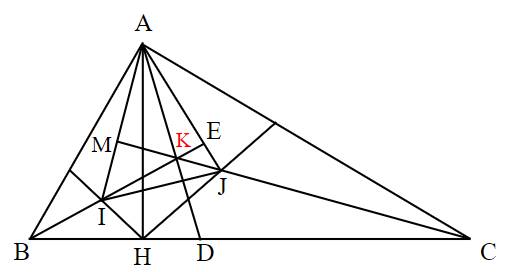
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)

Ta có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC < AB + BC + CA (vì OC < BC) Vậy ta có: OA + OB + OC < AB + BC + CA (1) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OC) + OB = AC + OB < AB + BC + CA (vì OB < AB) Vậy ta có: OA + OB + OC < AB + BC + CA (2) Từ (1) và (2), ta có: OA + OB + OC < AB + BC + CA Tương tự, ta có: OA + OB + OC = OA + OB + OC = (OB + OC) + OA = BC + OA > 0A + OB + OC (vì BC > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (3) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC > 0A + OB + OC (vì AB > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (4) Từ (3) và (4), ta có: OA + OB + OC > 0A + OB + OC Vậy ta có: 0A + OB + OC < AB + BC + CA < OA + OB + OC

Lời giải:
$(-3)^5 = -243$
$(\frac{-1}{3})^5=\frac{(-1)^5}{3^5}=\frac{-1}{243}$
$(0,1)^3=0,001$
$10^3=1000$
$(\frac{2}{5})^2=\frac{2^2}{5^2}=\frac{4}{25}=0,16$
$(-1)^{200}=1$
$\frac{5^6.6^6}{30^4}=\frac{(5.6)^6}{30^4}=\frac{30^6}{30^4}=30^2=900$
$\frac{3^2.12^2}{6^4}=\frac{3^2.2^2.6^2}{6^4}=\frac{(3.2)^2.6^2}{6^4}$
$=\frac{6^2.6^2}{6^4}=\frac{6^4}{6^4}=1$
$\frac{2^{15}.9^4}{6^6.8^3}=\frac{2^{15}.(3^2)^4}{2^6.3^6.(2^3)^3}$
$=\frac{2^{15}.3^{8}}{2^6.3^6.2^9}=\frac{2^{15}.3^8}{2^{15}.3^6}=\frac{3^8}{3^6}=3^2=9$

\(A=\left(a-b\right)-\left(c-a\right)+\left(-a+b+c\right)\)
\(A=a-b-c+a-a+b+c=a\left(1\right)\)
\(B=-\left(b-c\right)+\left(b-c+a\right)\)
\(B=-b+c+b-c+a=a\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow A=B=a\)

Để tìm giá trị của B, chúng ta cần tính tổng bình phương của các số chẵn từ 2 đến 30. Chúng ta có thể nhận thấy mỗi số trong dãy là một số chẵn và hiệu số chung giữa các số là 2. Do đó, chúng ta có thể viết lại dãy như sau: 2^2 + 4^2 + 6^2 + 8^2 + ... + 30^2 = (2^2) + (4^2) + (6^2) + (8^2) + ... + (30^2) Bây giờ, chúng ta có thể rút gọn 2^2 từ mỗi số: = 2^2(1 + 2^2 + 3^2 + 4^2 + ... + 15^2) Bây giờ, chúng ta cần tìm tổng bình phương của 15 số tự nhiên đầu tiên. Điều này có thể được thực hiện bằng cách sử dụng công thức tổng bình phương của n số tự nhiên đầu tiên: 1^2 + 2^2 + 3^2 + ... + n^2 = (n(n + 1)(2n + 1))/6 Thay n = 15 vào, chúng ta có: 1^2 + 2^2 + 3^2 + ... + 15^2 = (15(15 + 1)(2(15) + 1))/6 = (15(16)(31))/6 = 15(8)(31) = 3720 Bây giờ, chúng ta có thể thay giá trị này vào phương trình ban đầu: 2^2(1 + 2^2 + 3^2 + 4^2 + ... + 15^2) = 2^2(3720) = 4(3720) = 14880 Vì vậy, giá trị của B là 14880.

Lời giải:
Gọi tổng trên là $K$
$K=1+5^2+5^3+5^4+...+5^{200}$
$5K=5+5^3+5^4+5^5+...+5^{201}$
$\Rightarrow 5K-K = 5+5^{201}-1-5^2$
$\Rightarrow 4K = 5^{201}-21$
$\Rightarrow K= \frac{5^{201}-21}{4}$
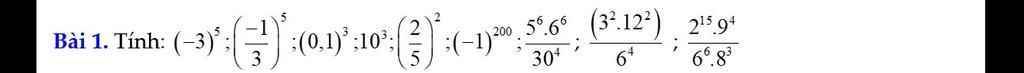
a) Ta có: HA = 2RcosA HB = 2RcosB HC = 2RcosC AB = 2RsinC AC = 2RsinB Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2RsinC + 2RsinB Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < sinC + sinB Áp dụng bất đẳng thức tam giác, ta có: sinC + sinB > sin(A + B) = sinCOSA + cosCSINA = cosA + cosB Vậy ta có: cosA + cosB + cosC < sinC + sinB Do đó, ta có HA + HB + HC < AB + AC. b) Ta có: AB + BC + CA = 2R(sinA + sinB + sinC) = 2R(sinA + sinB + sin(A + B)) = 2R(2sin(A + B/2)cos(A - B/2) + sin(A + B)) = 4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B) Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2332 (4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B)) Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) Áp dụng bất đẳng thức tam giác, ta có: sin(A + B) > sinC = sin(A + B/2 + B/2) = sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) Vậy ta có: 2sin(A + B/2)cos(A - B/2) + sin(A + B) < 2sin(A + B/2)cos(A - B/2) + sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + sin(B/2)cos(A + B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2)) Vậy ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) < 1166(sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2))) Do đó, ta có HA + HB + HC < 2332(AB + BC + CA).