cho hỏi x+y hay trừ y vậy bạn nếu trừ y bạn vào link này tham khảo nha https://olm.vn/hoi-dap/detail/30180926368.html

ta x+y=-95
=>x=-95-y
x.y=2016
=> (-95-y)y=2016
=>-95y-y^2-2016=0
=>y^2+95y+2016=0
=>y^2+32y+63y+2016=0
=>y(y+32)+63(y+32)=0
=>(y+63)(y+32)=0
=>y=-63 hoặc y=-32
=>x=-32 hoặc x=-63
Vậy x=-32 và y=-63 hoặc x=32,y=63 hoặc x=63,y=32 hoặc x=-63,y=-32

\(\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{a+b-c+2c}{a+b-c}=\frac{a-b-c+2c}{a-b-c}=1+\frac{2c}{a+b-c}=1+\frac{2c}{a-b-c}\)

\(\Leftrightarrow\frac{2c}{a+b-c}=\frac{2c}{a-b-c}\Leftrightarrow\orbr{\begin{cases}c=0\\a+b-c=a-b-c\end{cases}\Leftrightarrow\orbr{\begin{cases}c=0\\b-c=-b-c\end{cases}\Leftrightarrow}\orbr{\begin{cases}c=0\\b=0\left(loai\right)\end{cases}}}\)

câu 1 thì b áp dụng t.c là ra

x+y=5x-5y

=>4x=6y

=>2x=3y=>x/3=y/2=>x/y=3/2

Đến đây bạn ra rồi x+y=3/2; 5(x-y) = 3/2

Vô vàn cách tìm x;y

x+y=5(x-y) hay x+y=5x-5y 

                       5x-x=y+5y 

                       4x=6y nên x=1,5y

Thay x=1,5y vào x+y=x:y ta có:

1,5y+y=1,5y:y

2,5y=1,5

y=0,6 nên x=1,5x0,6=0,9

 Vậy x=0,9 ;y=0,6

Đây là các bước để giải hai câu trên bn tham khảo nha:
1. Chứng minh góc BEH = góc ACB.
2. Chứng minh DH = DC = DA.
3. Lấy B' sao cho H là trung điểm của BB'. Chứng minh tam giác AB'C cân.
4. Chứng minh AE = HC

Chúc bn học tốt~~

Ảnh đây

oh minecratf  kìa

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)=> \(\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)

Khi đó, ta có: \(\frac{\left(bk\right)^2+\left(bk\right)\left(dk\right)}{\left(dk^2\right)-\left(bk\right)\left(dk\right)}=\frac{b^2.k^2+b.d.k^2}{d^2.k^2-b.d.k^2}=\frac{\left(b^2+bd\right).k^2}{\left(d^2-bd\right).k^2}=\frac{b^2+bd}{d^2-bd}\)

Vậy ...

hok trường chuyên mak dell bt bài ni ak:))

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)

\(\Rightarrow a=bk;c=dk\)

Thay vào ta được:\(\frac{7a^2+5ac}{7a^2-5ac}=\frac{7b^2k^2+5bk\cdot dk}{7b^2k^2-5bk\cdot dk}=\frac{bk^2\left(7b+5d\right)}{bk^2\left(7b-5d\right)}=\frac{7b+5d}{7b-5d}\left(1\right)\)

\(\frac{7b^2+5bd}{7b^2-5bd}=\frac{b\left(7b+5d\right)}{b\left(7b-5d\right)}=\frac{7b+5d}{7b-5d}\left(2\right)\)

Từ (1) và (2) \(\Rightarrowđpcm\)

Ta có : a/b = c/d => a/c = b/d

Đặt \(\frac{a}{c}=\frac{b}{d}=k\) => \(\hept{\begin{cases}a=ck\\b=dk\end{cases}}\)

Khi đó, ta có: \(\frac{7.\left(ck\right)^2+5c^2k}{7\left(ck\right)^2-5c^2k}=\frac{7.c^2.k^2+5.c^2.k}{7.c^2.k^2-5.c^2.k}=\frac{\left(7k+5\right).c^2.k}{\left(7k-5\right).c^2.k}=\frac{7k+5}{7k-5}\)(1)

                     \(\frac{7.\left(dk\right)^2+5.d^2.k}{7\left(dk\right)^2-5.d^2.k}=\frac{7.d^2.k^2+5.d^2.k}{7.d^2.k^2-5.d^2.k}=\frac{\left(7k+5\right).d^2.k}{\left(7k-5\right).d^2.k}=\frac{7k+5}{7k-5}\) (2)

Từ (1) và (2) suy ra (Đpcm)

cộng cả 2 vế của 3 đẳng thức cùng chiều ta có: x + y - z + x - y + z + -x + y + z = a - b + b - c + c - a

                                                                          =>(x + x - x ) + (y - y + y) + (z + z - z) = 0

                                                                          => x + y + z =0 (đpcm)

54. Đoạn lên dốc từ C đến A dài 8.5cm, đô dài CB bằng 7,5cm.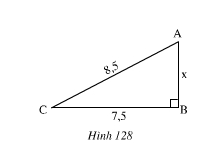

Tính chiều cao AB.

Theo địnhlípytago, ta có:

AB2 + BC2 = AC2

nên AB2 = AC2 – BC2

= 8,52 – 7,52

= 72,5-56,5=16

Vậy AB= 4

Bài 55 trang 131.Tính chiều cao của bức tường(h.129) biết rằng chiều cao của thang là 4m và chân thang cách tường 1m.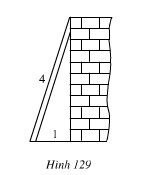

Theo đL pytago, ta có:

AC2+ BC2 = AB2

nên AC2 = AB2+BC2

Suy ra LAD = √15 ≈ 3.87

Luyện tập 1: 

Bài 56 Toán 7 tập 1. Tam giác nào là Δvuông trong các Δcó độ dài ba cạnh như sau:

a) 9cm,15cm,12cm.

b) 5dm,13dm,12cm.

c)7m,7m,10m.

Đáp án: a) Ta có 92 = 81,152 = 225, 122 =144.

mà 225=81+144

hay 152=92+122.

Nên Δ có độ dài ba cạnh 9cm,15cm,12cm là Δ vuông.

b) Ta có 52=25,132=169,122=144.

Mà  169=25+144 nên Δ có độ dài ba cạnh 5dm, 13dm,12dm là Δvuông

c) Ta có 72=49, 102=100

vậy 72+ 72 ≠102

72+102 ≠72

Nên Δ có độ dài 3 canh là 7dm,7dm,10dm không phải là Δvuông.

Bài 54:

Theo định lí Pytago, ta có:

AB2+BC2=AC2

nên AB2=AC2–BC2

\(8.5^2-7.5^2\)

=72,5−56,5=16=

Vậy Ab =4 cm

Bài 55:

Theo đL pytago, ta có:

AC2+ BC2 = AB2

nên AC2 = AB2+BC2

Suy ra LAD = √15 ≈ 3.8

Bài 56:

 a) Ta có 92 = 81,152 = 225, 122 =144.

mà 225=81+144

hay 152=92+122.

Nên Δ có độ dài ba cạnh 9cm,15cm,12cm là Δ vuông.

b) Ta có 52=25,132=169,122=144.

Mà  169=25+144 nên Δ có độ dài ba cạnh 5dm, 13dm,12dm là Δvuông

c) Ta có 72=49, 102=100

vậy 72+ 72 ≠102

72+102 ≠72

Nên Δ có độ dài 3 canh là 7dm,7dm,10dm không phải là Δvuông

a) \(2x=3y\Rightarrow\frac{x}{3}=\frac{y}{2}\) (1)

     \(3y=5z\Rightarrow\frac{y}{5}=\frac{z}{3}\) (2)

Từ (1);(2) suy ra: \(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)

Theo đề: \(\left|x-2y\right|=5\)

\(\Rightarrow x-2y=5\) (nếu \(x-2y\ge0\Leftrightarrow x\ge2y\) )

    \(x-2y=-5\) (nếu \(x< 2y\) )

Vậy có hai trường hợp

TH1: Nếu \(x\ge2y\) suy ra: \(\frac{x}{15}=\frac{y}{10}\Rightarrow\frac{x}{15}=\frac{2y}{20}=\frac{x-2y}{15-20}=\frac{5}{-5}=-1\)

\(\Rightarrow\hept{\begin{cases}x=15.\left(-1\right)=-15\\y=10.\left(-1\right)=-10\\z=6.\left(-1\right)=-6\end{cases}}\) (nhận)

TH2: Nếu x < 2y suy ra: \(\frac{x}{15}=\frac{y}{10}\Rightarrow\frac{x}{15}=\frac{2y}{20}=\frac{x-2y}{15-20}=\frac{-5}{-5}=1\)

\(\Rightarrow\hept{\begin{cases}x=15.1=15\\y=10.1=10\\z=6.1=6\end{cases}}\) (nhận)

b) \(5x=2y\Rightarrow\frac{x}{2}=\frac{y}{5}\) (1)

    \(2x=3z\Rightarrow\frac{x}{3}=\frac{z}{2}\) (2)

Từ (1);(2) => \(\frac{x}{6}=\frac{y}{15}=\frac{z}{10}\)

Đặt \(\frac{x}{6}=\frac{y}{15}=\frac{z}{10}=k\)

\(\Rightarrow\hept{\begin{cases}x=6k\\y=15k\\z=10k\end{cases}\Rightarrow xy=6k.15k=90k^2=90\Rightarrow k^2=1\Rightarrow k=\left\{-1;1\right\}}\)

\(\Rightarrow\hept{\begin{cases}x=6.1=6\\y=15.1=15\\z=10.1=10\end{cases}}\) hoặc \(\hept{\begin{cases}x=6.\left(-1\right)=-6\\y=15.\left(-1\right)=-15\\z=10.\left(-1\right)=-10\end{cases}}\)

c) Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

\(\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{1}{x+y+z}\)

= \(\frac{y+z+1+x+z+2+x+y-3}{x+y+z}\)

= \(\frac{2x+2y+2z}{x+y+z}\)

= \(\frac{2\left(x+y+z\right)}{x+y+z}=2\)

=> \(\frac{1}{x+y+z}=2\) => x + y + z = 1/2

=> \(\frac{y+z+1}{x}=2\) => y + z + 1 = 2x 

                                       => y + z + x + 1 = 3x

                                       => 1/2 + 1 = 3x

                                      => 3/2 = 3x

                                      => x = 3/2 : 3 = 1/2

=> \(\frac{x+z+2}{y}=2\) => x + z + 2 = 2y

                                        => x + z + y + 2 = 3y

                                        => 1/2 + 2 = 3y

                                       => 5/2 = 3y

                                       => y = 5/2 : 3 = 5/6

=> \(\frac{x+y-3}{z}=2\)=> x + y - 3 = 2z

                                         => x + y + z - 3 = 3z

                                          => 1/2 - 3 = 3z

                                        => 3z = -5/2

                                         => z = -5/2 : 3 = -5/6

Vậy ...