Ta có :
     BAC+ABC+ACB=180(Theo định lí tổng 3 góc)
     BAC+45+120=180
     BAC =180-(120+45)
     BAC = 15
Kẻ ED vuông góc với AC và vẽ điểm F sao cho C là trung điểm của BF
Ta có:
     BCA = 120
=> ACD = 60(2 góc kề bù)
Vì tam giác CED vuông tại E
=> EN=CN=DN
Vậy tam giác ECD cân tại N Vi ACD = 60
=> ECD là tam giác đều
=> BC=CE(cm ) 
Tam giác BCE Cân tại C
     EBD=30
Xét tam giác ECD vuông tại E có
     EDB= 30 (tổng 3 góc)
Vậy EBD cân tại E
=> EB=ED ABE+EBD=ABD ABE+30=45
ABE= 15
hay BAC=15
=> BA=BE
Tam giác ABE cân tại E
Mà BE=BD
=> AE=DE
=> AED = 90
Tam giác AED vuông cân
EDA = 45 °
Tính ra BDA= 75°

EN=CN=DN ? Copy hả bạn ?

A, \(C=\left(x+2\right)^2+\left(\frac{y}{5}\right)^2-10\)

mà \(\left(x+2\right)^2\ge0,\left(\frac{y}{5}\right)^2\ge0\)

\(C=\left(x+2\right)^2+\left(\frac{y}{5}\right)^2-10\ge-10\)

Vậy C đạt GTNN là -10 khi \(\left(x+2\right)^2=0và\left(\frac{y}{5}\right)^2=0\)

\(\Leftrightarrow\hept{\begin{cases}x=-2\\y=0\end{cases}}\)

B, Vì \(4>0\)và\(\left(2x-3\right)^2+5>0\)

Nên \(D=\frac{4}{\left(2x-3\right)^2+5}\)có GTLN khi (2x-3)²+5 đạt GTNN

\(\left(2x-3\right)^2+5\ge5\)

\(\Rightarrow\left(2x-3\right)^2+5\)có GTNN là 5 khi 2x-3=0 => x=3/2

Thay vào D ta có: \(D=\frac{4}{5}\)

Vâỵ \(D_{max}=\frac{4}{5}\)khi\(x=\frac{3}{2}\)

chị tự kẻ hình : 

AH _|_ BC (gt) => góc DHA = 90^o (đn)

=> góc ADH + góc DHA + góc DAH = 180 (đl)

=> góc ADH + 90 + góc DAH  = 180

=> góc ADH = 180 - 90 - góc DAH 

=> góc ADH = 90 - góc DAH                  (1)

có tam giác ABC vuông tại A (gt) 

=> góc DAB + góc CAD = 90 

=> góc DAB = 90 - góc CAD              (2)

AD là phân giác của góc HAC (gt) => góc CAD = góc DAH (đn)            (3)

(1)(2)(3) => góc DAB = góc ADB 

=> tam giác ABD cân tại B (dh)

Ta có: \(\widehat{CAD}=\widehat{BAC}-\widehat{BAD}=90^0-\widehat{BAD}\)

\(\widehat{HAD}=90^0-\widehat{BDA}\)

Mà \(\widehat{CAD}=\widehat{HAD}\) (vì AD là tia phân giác của góc HAC)

Do đó: \(\widehat{BAD}=\widehat{BDA}\Rightarrow\Delta ABD\) cân tại B

Chúc bạn học tốt.

cảm ơn

                           Giải

Gọi số viên bi của ba bạn Minh, Hùng ,Dũng lần lượt là x (viên bi), y (viên bi), z (viên bi).

Số bi của Minh, Hùng, Dũng tỉ lệ với các số 2, 4, 5 nghĩa là \(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}\)

Ba bạn có tất cả 44 viên bi nghĩa là x + y + z = 44.

Theo tính chất của dãy tỉ số bằng nhau ta có :

\(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{2+4+5}=\frac{44}{11}=4\)

\(\Rightarrow\frac{x}{2}=4\Leftrightarrow x=4.2\Leftrightarrow x=8\)

\(\Rightarrow\frac{y}{4}=4\Leftrightarrow y=4.4\Leftrightarrow y=16\)

\(\Rightarrow\frac{z}{5}=4\Leftrightarrow z=5.4\Leftrightarrow z=20\)

Vậy số viên bi của Minh, Hùng, Dũng lần lượt là 8, 16, 20 viên bi.

Gọi số bi của 3 bạn lần lượt là a,b,c ( a,b,c thuộc N* )

Theo đề bài ra ta có :

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\)

Theo t/c của dãy tỉ số bằng nhau

\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{2+4+5}=\frac{44}{11}=4\)

\(\hept{\begin{cases}a=4.2=8\\b=4.4=16\\c=5.4=20\end{cases}}\)

vậy

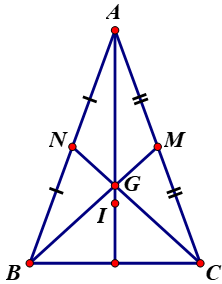
                             Giải

- Gọi M, N là trung điểm CA và BA.

ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.

⇒ BM = CN ( chứng minh ở bài 26)

Mà \(GB=\frac{2}{3}BM;GC=\frac{2}{3}CN\)(Tính chất trọng tâm của tam giác)

⇒ GB = GC

- ΔAGB và ΔAGC có

AG chung

AB = AC (do ΔABC cân tại A)

GB = GC (chứng minh trên)

⇒ ΔAGB = ΔAGC (c.c.c)

\(\Rightarrow\widehat{BAG}=\widehat{CAG}\)( hai góc tương ứng )

\(\Rightarrow\)G là trọng tâm của \(\widehat{BAC}\)

- Theo đề bài I cách đều ba cạnh của tam giác

Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác

⇒ I thuộc tia phân giác của \(\widehat{BAC}\)

Vì G, I cùng thuộc tia phân giác của  \(\widehat{BAC}\)nên A, G, I thẳng hàng

\(S_{MNPB}=NP^2=441\Rightarrow NP=21\left(cm\right)\)

MNPB là hình vuông (gt) nên NP = MB = 1/2 AB

\(\Rightarrow\frac{1}{2}AB=21\Rightarrow AB=42\left(cm\right)\)

Áp dụng định lí pitago, ta có: 

     \(BA^2+BC^2=AC^2\)

\(\Rightarrow2AB^2=AC^2\)

\(\Rightarrow AC^2=2.42^2\Rightarrow AC=42\sqrt{2}\left(cm\right)\)

ko đăng câu hỏi linh tinh bn nhá!