Cho hình thang ABCD có AB//CD, AB<CD, đường chéo BD vuông góc với cạnh BC. Kẻ BH vuông góc với CD. Tính diện tích hình thang ABCD biết BC=15cm, DC= 25cm. (ABCD ko phải hình thang cân)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x=1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}=1+\frac{1}{1+\frac{1}{\frac{3}{2}}}=1+\frac{1}{1+\frac{2}{3}}+1+\frac{1}{\frac{5}{3}}=1+\frac{3}{5}=\frac{8}{5}\)
\(y=1-\frac{1}{1-\frac{1}{1-\frac{1}{2}}}=1-\frac{1}{1-\frac{1}{\frac{1}{2}}}=1-\frac{1}{1-2}=1-\frac{1}{-1}=1+1=2\)
Suy ra \(x-y=\frac{8}{5}-2=-\frac{2}{5}\)
\(x+y=\frac{8}{5}+2=\frac{18}{5}\)

Gọi khoảng cách giữa hai bến A và B là x ( km), ĐK: x > 0 .
Khi đó: Vận tốc của ca nô đi từ A đến B là : x5x5(km/h)
Vận tốc của ca nô đi từ B đến A là : x7x7 (km/h)
Theo đề ra ta có phương trình: 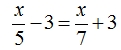
Giải phương trình và đến kết quả x = 105 ( thoả mãn)
Vậy khoảng cách giữa hai bến A và B là 105 km.
gọi vận tốc của tàu là v. (v>3)
khi đó vận tốc thực của tàu khi đi từ a đến b là v+3(km)
suy ra AB=5x(v+3) (1)
vận tốc thực của tàu khi đi từ b về a là v-3 (km)
suy ra AB=7x(v-3) (2)
từ (1) (2) có: v=18 km (tm)

Ta có : \(7a^2+b^2=8ab\)
<=> \(7a^2-7ab+b^2-ab=0\)
<=> \(7a\left(a-b\right)-b\left(a-b\right)=0\)
<=> \(\left(7a-b\right)\left(a-b\right)=0\)
<=> \(\orbr{\begin{cases}a=\frac{b}{7}\\a=b\end{cases}}\)
Với \(a=\frac{b}{7}\) => \(M=1+\frac{b}{\frac{b}{7}}=1+7=8\)
Với a = b => \(M=1+1=2\)

\(\frac{1}{x}=\frac{1}{y}=\frac{1}{z}=1\)
\(\Leftrightarrow x=y=z=1\)
vậy nghiệm nguyên của pt là : \(\left(x,y,z\right)=1\)
Nếu \(z\ge y\ge x\ge1\) thì
_ \(x=\frac{1\Rightarrow1}{y}+\frac{1}{z}=0\)( Ko thỏa mãn )
_ \(x=2\Rightarrow\frac{1}{y}+\frac{1}{z}=2\)\(\Rightarrow2y+2z=yz\Rightarrow\left(y-2\right)\left(z-2\right)=4\)
ta xét các trường hợp :
\(\hept{\begin{cases}y-2=1\\z-2=4\end{cases}\Leftrightarrow\hept{\begin{cases}y=3\\z=6\end{cases}}}\)
Hoặc \(\hept{\begin{cases}y-2=2\\z-2=2\end{cases}\Leftrightarrow\hept{\begin{cases}y=4\\z=4\end{cases}}}\)
_ Nếu \(x=3\Rightarrow\frac{1}{y}+\frac{1}{z}=\frac{2}{3}\)
_ Nếu \(x=3\Rightarrow y=3\)
_ Nếu \(y\ge4\Rightarrow\frac{1}{y}+\frac{1}{z}+\frac{1}{x}\le\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4}\)( Mà \(\frac{3}{4}< 1\)) ( Ko thỏa mãn )
Vậy tự kết luận

1)
Ta có : \(m_X=1,225\times32=39,2\left(g\right)\)
Giả sử có 1 mol X , gọi số mol của \(CO_2\)là a
Ta có : \(n_{N_2}=1-a\left(mol\right)\)
Ta có phương trình sau :
\(44a+28\left(1-a\right)=39,2\)
\(\Leftrightarrow44a+28-28a=39,2\)
\(\Leftrightarrow16a=11,2\)
\(\Leftrightarrow a=0,7\)
Vậy số mol của \(CO_2\) trong hỗn hợp X là 0,7 mol
\(\Rightarrow n_{N_2}=1-0,7=0,3\left(mol\right)\)
\(\Rightarrow\hept{\begin{cases}\%n_{CO_2}=70\%\\\%n_{N_2}=30\%\end{cases}}\)
Mà ở cùng một điều kiện về nhiệt đọ và áp suất, tỉ lệ số mol bằng tỉ lệ về thể tích
\(\Rightarrow\hept{\begin{cases}\%V_{CO_2}=70\%\\\%V_{N_2}=30\%\end{cases}}\)
Vậy \(\%V_{N_2}\) trong hỗn hợp X là 30%
AB = ?????? bao nhiêu hã bạn