ĐKXĐ : \(x\ge-\dfrac{3}{8}\)

Ta có : \(\sqrt{8x+3}=9x^2+10x+\dfrac{9}{4}\)

\(\Leftrightarrow36x^2+40x+9-4\sqrt{8x+3}=0\)

\(\Leftrightarrow\left(36x^2+48x+16\right)-8x-3-4\sqrt{8x+3}-4=0\)

\(\Leftrightarrow\left(6x+4\right)^2-\left(\sqrt{8x+3}+2\right)^2=0\)

\(\Leftrightarrow\left(6x+\sqrt{8x+3}+6\right).\left(6x+2-\sqrt{8x+3}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{8x+3}=-6x-6\left(1\right)\\\sqrt{8x+3}=-6x-2\left(2\right)\end{matrix}\right.\)

Giải (1) ta có :

(1) <=> \(8x+3=\left(-6x-6\right)^2\) (với \(-6x-6\ge0\Leftrightarrow x\le-1\))

\(\Leftrightarrow36x^2+64x+33=0\)

\(\Leftrightarrow\left(6x+\dfrac{16}{3}\right)^2+\dfrac{41}{9}=0\)

\(\Leftrightarrow x\in\varnothing\) => (1) vô nghiệm

Giải (2) ta có 

(2) <=> \(8x+3=\left(-6x-2\right)^2\) (với \(x\le-\dfrac{1}{3}\)) (*)

\(\Leftrightarrow36x^2+16x+1=0\)

\(\Leftrightarrow x=\dfrac{-4\pm\sqrt{7}}{18}\) 

Kết hợp (*) và ĐKXĐ ta được \(x=\dfrac{-4+\sqrt{7}}{18}\) là nghiệm phương trình

Bài này Phải dùng sơ đồ ven em nhé. Số chia hết cho 3 hoặc 5 gồm những số chỉ chia hết cho 3; chỉ chia hết cho 5 và những số chia hết cho cả 3 và 5.

                              Bài Gải 

Những số tự nhiên chia hết cho 3 mà nhỏ hơn 200 là các số thuộc dãy số sau: 0; 3; 6; 9; 12; 15;....;198

Số các số tự nhiên chia hết cho 3 mà nhỏ hơn 200 là: 

                  ( 198 - 0) : 3 + 1 = 67 ( số)

Các số tự nhiên chia hết cho 5 mà nhỏ hơn 200 là các số thuộc dãy số sau:  0; 5; 10; 15;....195

Số các số tự nhiên chia hết cho 5 mà nhỏ hơn 200 là:

                ( 195 - 0) : 5 + 1 = 40 ( số)

Các số tự nhiên chia hết cho cả 3 và 5 mà nhỏ hơn 200 là các số thuộc dãy số sau:

      0; 15; 30;...;195

Số các số tự nhiên chia hết cho 15 mà nhỏ hơn 200 là:

      ( 195 - 0) : 15 + 1 = 14 ( số)

Coi các số chia hết cho 3 là một vòng tròn (1)

Coi các số chia hết cho 5 là một vòng tròn nữa ( 3)

Ta có sơ đồ: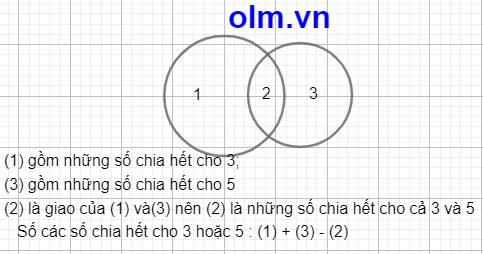 

Theo sơ đồ ta có Số các số chia hết cho 3 hoặc 5 là:

              67 + 40 - 14 = 93 ( số) 

Đáp số: 93 số 

Các số chia hết cho 5 nhỏ hơn 200

0; 5; 10; ....195

Các số chia hết cho 3 nhở hơn 200:

0; 3; 6; ... 1998

Tổng số lượng các số ở 2 dãy trên là số cần tìm

Đề chưa đủ cơ sở dữ kiện

12 m =1200 cm 9 m = 900 cm

Diện tích viên gạch là: 60 x 60 = 3600 (cm)

Diện tích căn phòng là : 1200 x 900 = 10800 (cm)

Vậy cần số gạch là: 10800 : 3600 = 3 (viên gạch)

3 viên gạch

ko biết b phủ thuộc vào bài toán

ko bt B phụ thuộc vào bài toán

Gọi 2 số càn tìm là a và b

Ta có a x b = 2,55 (1)

 (a + 1,2) x b = 4,35

<=> a x b + 1,2 x b = 4,35 (2)

Thay  (1) vào (2) ta có

2,55 + 1,2 x b = 4,35

=> 1,2 x b = 4,35 -2,55

=> 1,2 x b = 1,8

=>         b  = 1,8 : 1,2

=>          b  = 1,5 (3)

Thay (3) vào (1)

=> a x 1,5 = 2,55

=> a          = 2,55 : 1,5

=> a          = 1,7

Vậy a = 1,7

       b = 1,5

a) = ( 5,4 - 4,4 ) + ( 6,5 - 5,5 ) + ( 7,6 - 6,6 ) + ( 8,7 - 7,7 )

    =  1 + 1 + 1 + 1

    = 4

b) = 9/10